ņé¼ņ╝Ćļ”¼-ļź┤ņןļō£ļź┤ ņĀĢļ”¼
|
Read other articles:

Charles de LannoyBiografiKelahirank. 1487 (Kalender Masehi Gregorius) Valenciennes Kematian23 September 1527 (Kalender Masehi Gregorius) (39/40 tahun)Gaeta (en) Tempat pemakamanSant'Anna dei Lombardi (en) Caballerizo mayor del rey (en) KegiatanPekerjaanPrajurit dan personel militer Pangkat militerJenderal KonflikPeperangan Italia KeluargaKeluargaWangsa de Lannoy AnakPhilip de Lannoy, 1st Prince of Sulmona (en)Clemente de Lannoy, Baron di Prata (en)Giorgio de Lannoy, 2.D...
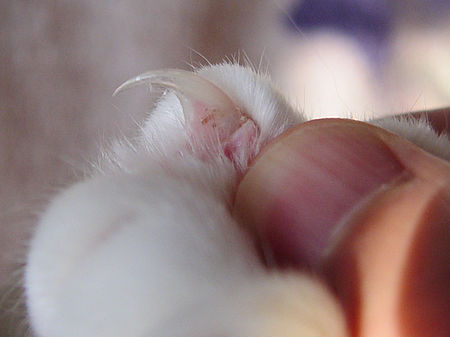
Gambaran kuku yang dapat ditarik kembali dari seekor kucing Cakar adalah anggota tambahan badan yang terlindung dari ujung kaki. Cakar sebenarnya adalah pembesaran dan pengerasan dari kuku.[1] Cakar dimiliki oleh berbagai Tetrapoda seperti Amfibi, Reptil, Burung dan Mamalia. Dalam Mamalia, Hewan berkuku disebut ungulata. Ungulata terbagi dalam 2 kelompok besar: hewan berkuku genap (misalnya antelop, sapi, rusa, babi, domba, kambing) dan hewan berkuku gasal (kuda, badak dan tapir). Hew...

ž¦┘äž╣┘䞦┘鞦ž¬ ž¦┘䞯┘åž║┘ł┘ä┘Ŗž® ž¦┘ä┘é┘Ŗž▒ž║┘Ŗž▓ž│ž¬ž¦┘å┘Ŗž® žŻ┘åž║┘ł┘䞦 ┘é┘Ŗž▒ž║┘Ŗž▓ž│ž¬ž¦┘å žŻ┘åž║┘ł┘䞦 ┘é┘Ŗž▒ž║┘Ŗž▓ž│ž¬ž¦┘å ž¬ž╣ž»┘Ŗ┘ä ┘ģžĄž»ž▒┘Ŗ - ž¬ž╣ž»┘Ŗ┘ä ž¦┘äž╣┘䞦┘鞦ž¬ ž¦┘䞯┘åž║┘ł┘ä┘Ŗž® ž¦┘ä┘é┘Ŗž▒ž║┘Ŗž▓ž│ž¬ž¦┘å┘Ŗž® ┘ć┘Ŗ ž¦┘äž╣┘䞦┘鞦ž¬ ž¦┘äž½┘垦ž”┘Ŗž® ž¦┘䞬┘Ŗ ž¬ž¼┘ģž╣ ž©┘Ŗ┘å žŻ┘åž║┘ł┘䞦 ┘ł┘é┘Ŗž▒ž║┘Ŗž▓ž│ž¬ž¦┘å.[1][2][3][4][5] ┘ģ┘鞦ž▒┘åž® ž©┘Ŗ┘å ž¦┘äž©┘äž»┘Ŗ┘å ┘ćž░┘ć ┘ģ┘鞦ž▒┘åž® ž╣ž¦┘ģž® ┘ł┘ģž▒ž¼ž╣┘Ŗ...

Species of flowering plant Senecio pulcher Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Asterids Order: Asterales Family: Asteraceae Genus: Senecio Species: S. pulcher Binomial name Senecio pulcherHook. & Arn.[1] Range of Senecio pulcher. Senecio pulcher is an ornamental plant native to the wet valleys & slopes and flooded rocky[2] habitats in Argentina, Brazil, and Uruguay. Cited in Flora Brasiliensis&#...

1999 studio album by Cosmic BabyHeavenStudio album by Cosmic BabyReleased1999Recorded1998GenreTechno, trance, house, chill-out, electro, Balearic beat, breakbeatLength77:19LabelIntercordCosmic Baby chronology Fourteen Pieces(1996) Heaven(1999) Die Toteninsel(2006) Heaven is a music album by techno/trance artist Cosmic Baby which was released in 1999. It is Cosmic Baby's fourth full-length album. It was his final album before his break from recording as Cosmic Baby, as well as his fina...

Ecclesiastical museum in the Philippines For the museum in Santa Ana, Manila, and former location of the first local congregation of the Iglesia ni Cristo, see Iglesia ni Cristo Museum (Santa Ana, Manila). Iglesia ni Cristo MuseumFormer nameIglesia ni Cristo Museum and GalleryEstablished1984 (1984)Location25 Central Avenue, New Era , Quezon City, PhilippinesTypeEcclesiastical museumCuratorBro. Cornelio Cortez, Jr.OwnerFelix Y. Manalo FoundationBuilding detailsGeneral informationInaugurat...

Pour les articles homonymes, voir Lindfors. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (janvier 2019). Si vous disposez d'ouvrages ou d'articles de r├®f├®rence ou si vous connaissez des sites web de qualit├® traitant du th├©me abord├® ici, merci de compl├®ter l'article en donnant les r├®f├®rences utiles ├Ā sa v├®rifiabilit├® et en les liant ├Ā la section ┬½ Notes et r├®f├®rences ┬╗. En pratique&#...

American politician Matt Pinnell17th Lieutenant Governor of OklahomaIncumbentAssumed office January 14, 2019GovernorKevin StittPreceded byTodd Lamb1st Oklahoma Secretary of Tourism and BrandingIn officeJanuary 18, 2019 ŌĆō March 1, 2024GovernorKevin StittPreceded byPosition establishedChair of the Oklahoma Republican PartyIn officeJune 26, 2010 ŌĆō April 20, 2013Preceded byGary JonesSucceeded byDave Weston[1] Personal detailsBorn (1979-08-15) August 15, 1979 (age...

Apel Manalagi Klasifikasi ilmiah Kingdom: Plantae Divisi: Tumbuhan berbunga|Angiospermae Kelas: Eudikotil Subkelas: Rosids Ordo: Rosales Famili: Rosaceae Genus: Malus(Linnaeus) Spesies: M. sylvestris Tata nama biologi Malus sylvestris Apel Manalagi (Malus sylvestris) atau di Indonesia dikenal sebagai Apel Malang atau Apel Batu,[1] adalah spesies buah berupa apel liar dari genus Malus. Nama ilmiahnya berarti Apel Hutan karena sering tumbuh secara liar di hutan dengan ketinggian atau i...

Cette page concerne l'ann├®e 1677 du calendrier gr├®gorien. Chronologies L'apoth├®ose de Louis XIV, Charles Le Brun. la peinture en 1677 sur CommonsDonn├®es cl├®s 1674 1675 1676 1677 1678 1679 1680D├®cennies :1640 1650 1660 1670 1680 1690 1700Si├©cles :XVe XVIe XVIIe XVIIIe XIXeMill├®naires :-Ier Ier IIe IIIe Chronologies th├®matiques Art Architecture, Arts plastiques (Dessin, Gravure, Peinture et Sculpture), (), Litt├®rature (),...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of tallest buildings in Manchester, New Hampshire ŌĆō news ┬Ę newspapers ┬Ę books ┬Ę scholar ┬Ę JSTOR (November 2015) (Learn how and when to remove this message) Manchester is a city in Hillsborough County in southern New Hampshire, United States. It has a population of over 115...

Kongres Amerika Serikat ke-16Gedung Kapitol (1827)Periode4 Maret 1819 ŌĆō 4 Maret 1821Anggota46 senator186 anggota dewan3 delegasi tanpa suaraMayoritas SenatDemokrat-RepublikPresiden SenatDaniel D. TompkinsMayoritas DPRDemokrat-RepublikKetua DPRHenry ClayJohn W. TaylorPres. Senat Pro TemporeJames BarbourJohn GaillardSesike-1: 6 Desember 1819 ŌĆō 15 Mei 1820ke-2: 13 November 1820 ŌĆō 3 Maret 1821ke-15 ŌåÉŌåÆ ke-17 Kongres Amerika Serikat Keenam Belas adalah sidang cabang legisla...

British entry for the Eurovision Song Contest 1993 Better the Devil You KnowSingle by Soniafrom the album Better the Devil You Know B-sideNot What I Call LoveReleased19 April 1993 (1993-04-19)[1]Length2:36LabelAristaSongwriter(s) Brian Teasdale Dean Collinson Producer(s)Nigel WrightSonia singles chronology Boogie Nights (1992) Better the Devil You Know (1993) Hopelessly Devoted to You (1994) Eurovision Song Contest 1993 entryCountryUnited KingdomArtist(s)Sonia EvansAsSo...

Peta India pada masa kebudayaan Weda. Kerajaan Kuru tampak di utara bersama beberapa kerajaan tetangga yang utama. Peta 16 Mahajanapada (Kerajaan besar) pada masa India Kuno, sekitar abad VII-III SM. Kerajaan Kuru termasuk dalam salah satu Mahajanapada. Dalam sastra dan wiracarita India Kuno, Kerajaan Kuru merupakan kerajaan yang diperintah oleh Wangsa Kuru, keturunan Sang Kuru. Tidak diketahui dengan pasti kapan kerajaan ini berdiri, dan hingga sekarang dikenal sebagai legenda dalam wiracari...

List of rivers in Kentucky (U.S. state). By drainage basin This list is arranged by drainage basin, with respective tributaries indented under each larger stream's name. All rivers in Kentucky flow to the Mississippi River, nearly all by virtue of flowing to its major tributary, the Ohio River. Also listed are some important tributaries to the few Kentucky rivers that originate in, or flow through, other states. Mississippi River Obion Creek Mayfield Creek Ohio River Ohio River Drainage Basi...

Quality of having unlimited power This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (June 2021) (Learn how and when to remove this message) Separation of Light from Darkness by Michelangelo Part of a series on theAttributes of God in Christianity Core attributes Omnibenevolence Omnipotence Omnipresence Omniscience Eternity Overarching attributes Aseit...

Theological attempt to resolve the problem of evil This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: idiosyncratic tone and presentation, especially in the biblical section. Please help improve this article if you can. (December 2023) (Learn how and when to remove this message) This article may require c...

Sculpture by Aurelio Teno Don QuixoteSculpture in 2006ArtistAurelio TenoYear1976 (1976)TypeBronzeDimensions4.6 m ├Ś 1.8 m ├Ś 3.7 m (15 ft ├Ś 6 ft ├Ś 12 ft)LocationKennedy Center, Washington, D.C., United StatesCoordinates38┬░53ŌĆ▓49ŌĆ│N 77┬░03ŌĆ▓17ŌĆ│W / 38.89693┬░N 77.05459┬░W / 38.89693; -77.05459OwnerNational Park Service Don Quixote is a 1976 sculpture by Aurelio Teno located at the northeas...

1996 video gameThe Hunchback of Notre Dame: Topsy Turvy GamesDeveloper(s)7th Level[1]Disney InteractivePlatform(s) Microsoft Windows Game Boy Release1996Genre(s)ActionMode(s)Single-player The Hunchback of Notre Dame: Topsy Turvy Games is a game that was released in 1996 by Disney Interactive for Microsoft Windows and Game Boy. It was the second title in the company's GameBreak! series after GameBreak! Timon and Pumbaa's Jungle Games.[2] Tiertex adapted the game for SNES, Game ...

ąäąĮč¢-ąÜą░ą╗ąĄ 45┬░20ŌĆ▓58ŌĆ│ ą┐ąĮ. čł. 36┬░36ŌĆ▓16ŌĆ│ čüčģ. ą┤. / 45.349449000028┬░ ą┐ąĮ. čł. 36.60455000002777837┬░ čüčģ. ą┤. / 45.349449000028; 36.60455000002777837ąÜąŠąŠčĆą┤ąĖąĮą░čéąĖ: 45┬░20ŌĆ▓58ŌĆ│ ą┐ąĮ. čł. 36┬░36ŌĆ▓16ŌĆ│ čüčģ. ą┤. / 45.349449000028┬░ ą┐ąĮ. čł. 36.60455000002777837┬░ čüčģ. ą┤. / 45.349449000028; 36.60455000002777837ąóąĖą┐čĆčā茹ĮąĖ ąĘą░ą╝ą║čā...




