등각순환우주론
|
Read other articles:

Wichita, KansasKota BenderaLambangJulukan: Cowtown, The Air Capital Of The WorldLokasi di negara bagian KansasNegaraAmerika SerikatNegara bagianKansasCountySedgwickDidirikan1863Diresmikan1870Pemerintahan • Wali kotaCarl Brewer (D)Luas • Kota165,9 sq mi (359,8 km2) • Luas daratan163,7 sq mi (351,6 km2) • Luas perairan3,2 sq mi (8,2 km2)Ketinggian1.299 ft (396 m)Populasi (2010)[1...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Hayrünnisa Gül Ibu Negara TurkiMasa jabatan28 Agustus 2007 – 28 Agustus 2014 PendahuluSemra SezerPenggantiEmine Erdoğan Informasi pribadiLahirHayrünnisa Özyurt18 Agustus 1965 (umur 58)Istanbul, TurkiKebangsaanTurkiSuami/istriAbdullah Gül (m. 1980)AnakAhmed Münir, Mehmed Emre dan KübraSunting kotak info • L • B Hayrünnisa Gül (pengucapan [ˌhajɾyˈnisa ˈɟyl]; née Özyurt, kelahiran 18 Agustus 1965 pada İstanbul)[1] adalah Ibu Negara Tur...

Cornelius Island is a small uninhabited island in Wickford Harbor, Narragansett Bay, Wickford, Rhode Island. History The land compromising Cornelius Island was originally connected to the mainland and was part of the Smith/Updike land holdings until it was sold in 1813. A channel was dug at some point in the land's history disconnecting it from the mainland. It is unclear after whom Cornelius Island was named.[1] The island was used in the 1960s for the deposition of dredged material....

Reservoir in Vermont and New Hampshire, US Comerford ReservoirA view across a short inlet in the Comerford ReservoirComerford ReservoirShow map of New HampshireComerford ReservoirShow map of VermontComerford ReservoirShow map of the United StatesLocationCaledonia County, Vermont; Grafton County, New HampshireCoordinates44°19′31″N 72°0′03″W / 44.32528°N 72.00083°W / 44.32528; -72.00083TypeReservoirPrimary inflowsConnecticut RiverPrimary outflowsConnecticut R...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2016. VG Airlines (kode maskapai IV) merupakan sebuah maskapai penerbangan yang didirikan tahun 2002 untuk mengopeerasikan penerbangan dari Belgia menuju Amerika Utara dalam awal kebangkrutan Sabena. Maskapai ini berubah nama menjadi Delsey Airlines selama beb...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

ألاكانوك الإحداثيات 62°41′05″N 164°38′42″W / 62.6847°N 164.645°W / 62.6847; -164.645 [1] تاريخ التأسيس 28 أكتوبر 1969 تقسيم إداري البلد الولايات المتحدة[2] خصائص جغرافية المساحة 102.494004 كيلومتر مربع102.494018 كيلومتر مربع (1 أبريل 2010)[3] ارتفاع 1 متر عدد ا...

Irish peer (died 1687) William BurkeEarl of ClanricardeArms of de Burgh/Burke of Clanricarde[a]Tenure1666–1687PredecessorRichard, 6th Earl of ClanricardeSuccessorRichard, 8th Earl of ClanricardeDied1687Spouse(s)1. Lettice Shirley2. Helen MacCartyIssueDetailRichard, John, & othersFatherWilliam BurkeMotherJoan O'Shaugnessy William Burke, 7th Earl of Clanricarde, PC (Ire) (English: /klænˈrɪkɑːrd/; klan-RIK-ard; died 1687), was an Irish peer who fought in his youth together wit...

American journalist (1947–2024) For other people with the same name, see Robert Edwards (disambiguation). Bob EdwardsEdwards in 2005BornRobert Alan Edwards(1947-05-16)May 16, 1947Louisville, Kentucky, U.S.DiedFebruary 10, 2024(2024-02-10) (aged 76)Arlington, Virginia, U.S.Spouses Joan Murphy Sharon Kelly Windsor Johnston (m. 2011) Children2CareerShowThe Bob Edwards ShowNetworkXM Satellite RadioTime slotMonday through Friday 8–9 AM ETShowBob Edwards WeekendNetworkPublic Radio Int...

Village in Alytus County, LithuaniaŠklėriaiVillageŠklėriaiCoordinates: 53°58′40″N 24°14′20″E / 53.97778°N 24.23889°E / 53.97778; 24.23889Country LithuaniaCounty Alytus CountyMunicipalityVarėna district municipalityEldershipMarcinkonys eldershipPopulation (2021[1]) • Total30Time zoneUTC+2 (EET) • Summer (DST)UTC+3 (EEST) Šklėriai is a village in Varėna district municipality, in Alytus County, southeastern Lit...

Israelite kingdom in the Southern Levant This article is about the historical Kingdom of Israel, that lay to the north of the Kingdom of Judah. For the Biblical, unified monarchy, see Kingdom of Israel (united monarchy). For other uses, see Kingdom of Israel. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kingdom of Israel Samaria �...
NGO based in Toronto This article may have been created or edited in return for undisclosed payments, a violation of Wikipedia's terms of use. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. (April 2021) International Union of Food Science and TechnologyAbbreviationIUFoSTFormation1962; 62 years ago (1962)TypeINGOHeadquartersCanadaRegion served WorldwideOfficial language English, FrenchPresidentAman Wirakartakusumah[...

Regular object in four dimensional geometry Octaplex redirects here. For the clotting factors concentrate, see Prothrombin complex concentrate. This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: Excessive explanatory footnotes, some of which include other explanatory footnotes, which include other explanatory footnotes, and so on. Linearize by trimming for brevity, inserting into main text, or spawning subarticle(s). Please help improve this artic...

هنيكل إتش إي 111معلومات عامةالنوع قاذفة قنابلبلد الأصل ألمانيا التطوير والتصنيعالصانع هاينكلسنة الصنع 1935الكمية المصنوعة 32سيرة الطائرةدخول الخدمة 1935انتهاء الخدمة 1945أول طيران 24 فبراير 1935الوضع الحالي منتهية الخدمةالخدمةالمستخدم الأساسي سلاح الجو الألمانيالخصائصالطو�...

彭诗梦 個人信息全名 彭诗梦出生日期 (1998-05-12) 1998年5月12日(26歲)出生地點 中华人民共和国江苏省盐城市[1]身高 178厘米(5英尺10英寸)[2]位置 守门员俱乐部信息現在所屬 江苏苏宁国家队‡年份 球隊 出场 (进球)2017– 中国 25 (0) ‡ 国家队出场次數和进球數最後更新於:2021年7月28日 彭诗梦(1998年5月12日—),女,江苏盐城人,中国足球运动员。她曾随...
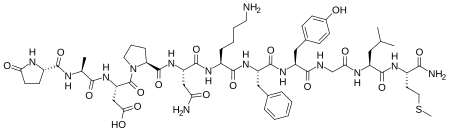
Physalaemin Names Other names H-Pyr-Ala-Asp-Pro-Asn-Lys-Phe-Tyr-Gly-Leu-Met-NH2 Identifiers CAS Number 2507-24-6 Y 3D model (JSmol) Interactive image ChEMBL ChEMBL415235 N IUPHAR/BPS 2094 MeSH Physalaemin PubChem CID 14717795 UNII H0T4KV6B9J Y CompTox Dashboard (EPA) DTXSID501043248 SMILES C[C@@H](C(=O)N[C@@H](CC(=O)O)C(=O)N1CCC[C@H]1C(=O)N[C@@H](CC(=O)N)C(=O)N[C@@H](CCCCN)C(=O)N[C@@H](CC2=CC=CC=C2)C(=O)N[C@@H](CC3=CC=C(C=C3)O)C(=O)NCC(=O)N[C@@H](CC(C)C)C(=O)N[C@@H](CCSC)C(=O)...
Town in Bács-Kiskun, HungaryJánoshalmaTown FlagCoat of armsJánoshalmaLocation of JánoshalmaCoordinates: 46°17′48″N 19°19′22″E / 46.29671°N 19.32283°E / 46.29671; 19.32283Country HungaryCountyBács-KiskunDistrictJánoshalmaArea • Total132.21 km2 (51.05 sq mi)Population (2008) • Total9,433 • Density74.48/km2 (192.9/sq mi)Time zoneUTC+1 (CET) • Summer (DST)UTC+2 (CEST)Postal code...

Book of history on the Maccabean Revolt Hebrew Bible (Judaism) Torah (Instruction)GenesisBereshitExodusShemotLeviticusWayiqraNumbersBemidbarDeuteronomyDevarim Nevi'im (Prophets) Former JoshuaYehoshuaJudgesShofetimSamuelShemuelKingsMelakhim Latter IsaiahYeshayahuJeremiahYirmeyahuEzekielYekhezqel Minor Hosea Joel Amos Obadiah Jonah Micah Nahum Habakkuk Zephaniah Haggai Zechariah Malachi Ketuvim (Writings) Poetic PsalmsTehillimProverbsMishleiJobIyov Five Megillot (Scrolls) Song of...

