문맥 자유 언어
|
Read other articles:

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Bandar Udara Internasional Curaçao – berita · surat kabar · buku · cendekiawan · JSTOR (July 2018) Bandara Internasional Curaçao Hato International AirportHato Internationale luchthavenIATA: CURICAO: TNCCIn...

Railway station in County Dublin, Ireland This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Rush and Lusk railway station – news · newspapers · books · scholar · JSTOR (February 2015) Rush and LuskAn Ros agus LuscaRush & Lusk railway station looking North in 2018.General informationLocationStatio...

New Hampshire gubernatorial election For related races, see 1810 United States gubernatorial elections. 1810 New Hampshire gubernatorial election ← 1809 March 13, 1810 1811 → Nominee John Langdon Jeremiah Smith Party Democratic-Republican Federalist Popular vote 16,325 15,166 Percentage 51.70% 48.03% Governor before election Jeremiah Smith Federalist Elected Governor John Langdon Democratic-Republican Elections in New Hampshire Federal government Presidential...

Eparki Katolik Siro-Malankara Mavelikara adalah sebuah eparki (keuskupan) suffragan dari Episkopal Agung Mayor Eparki Agung (Uskup Agung Metropolitan) Trivandrum, yang juga merupakan Uskup Agung Mayor (kepala) Gereja Katolik Siro-Malankara, Gereja Katolik Timur Ritus Antiokia di India. Tahtanya berada di Mavelikkara, sebuah taluk dan munisipalitas di bagian selatan distrik Alappuzha, negara bagian Kerala, barat daya India, di tepi Sungai Achankovil. Eparki tersebut adalah eparki ke-6 dari Ger...

كاليسبيل الإحداثيات 48°12′00″N 114°19′00″W / 48.2°N 114.31666666667°W / 48.2; -114.31666666667 [1] تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة فلاتهيد عاصمة لـ مقاطعة فلاتهيد خصائص جغرافية المساحة 30.877707 كيلومتر مربع30.358276 كيلومت�...

Extinct genus of dinosaurs VelocipesTemporal range: Late Triassic, 221.5–205.6 Ma PreꞒ Ꞓ O S D C P T J K Pg N Norian Fibula of the holotype Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Clade: Dinosauria Clade: Saurischia Clade: Eusaurischia Clade: Theropoda (?) Genus: †VelocipesHuene, 1932 Species: †V. guerichi Binomial name †Velocipes guerichiHuene, 1932 Velocipes (meaning quick foot) is a saurischian dinosaur genus from th...

Biathlon World Championships 2020Host cityRasen-AntholzCountryItalyEvents12Opening12 FebruaryClosing23 FebruaryOpened bySergio MattarellaMain venueSouth Tyrol ArenaWebsiteWebsite← Östersund 2019Pokljuka 2021 → Biathlon World Championships 2020IndividualmenwomenSprintmenwomenPursuitmenwomenMass startmenwomenRelaymenwomenMixed relaysingleteamvte The Biathlon World Championships 2020 took place in Rasen-Antholz, Italy, from 12 to 23 February 2020. Host selection On 4 Sept...
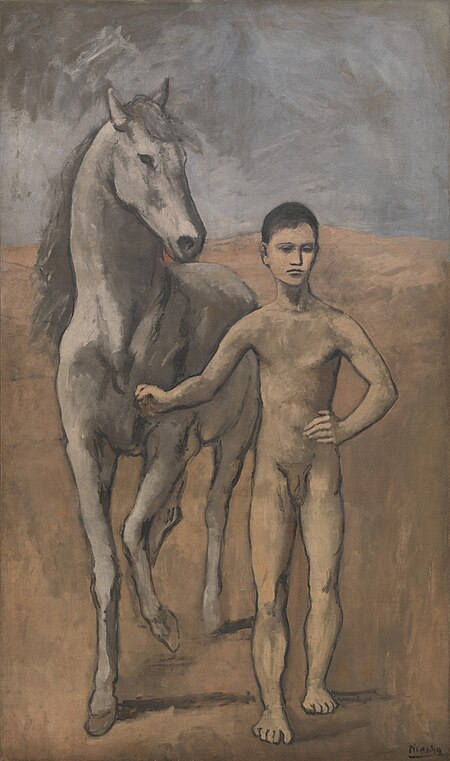
Painting by Pablo Picasso Boy Leading a HorseArtistPablo PicassoYear1905-1906Catalogue79994MediumOil on canvasMovementPicasso's Rose Period, ExpressionismDimensions220.6 cm × 131.2 cm (86.85 in × 51.65 in)LocationMuseum of Modern Art, New YorkAccession575.1964 Jeune garçon au cheval (English: Boy Leading a Horse) is an oil on canvas painting by Pablo Picasso. The painting is housed in the Museum of Modern Art in New York. It was painted in Picasso'...

Richard Herrmann Nazionalità Germania Germania Ovest (dal 1949) Altezza 167 cm Peso 68 kg Calcio Ruolo Attaccante Termine carriera 1960 Carriera Squadre di club1 1934-1945Katowice? (?)1945-1947 Kickers Offenbach? (?)1947-1960 FSV Francoforte? (?) Nazionale 1950-1954 Germania Ovest8 (1) Palmarès Mondiali di calcio Oro Svizzera 1954 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito...

U.S. Representative from Pennsylvania J. Roland KinzerMember of the U.S. House of Representativesfrom Pennsylvania's 9th districtIn officeJanuary 3, 1945 – January 3, 1947Preceded byCharles L. GerlachSucceeded byPaul B. DagueMember of the U.S. House of Representativesfrom Pennsylvania's 10th districtIn officeJanuary 28, 1930 – January 3, 1945Preceded byWilliam Walton GriestSucceeded byJohn W. Murphy Personal detailsBorn(1874-03-28)March 28, 1874Te...

French industrialist (1877–1944) Louis RenaultBorn(1877-02-12)12 February 1877Paris, FranceDied24 October 1944(1944-10-24) (aged 67)Fresnes Prison, Fresnes, FranceNationalityFrenchOccupationBusinessKnown forco-founder of RenaultRelativesMarcel Renault and Fernand RenaultAwardsLegion of Honor Louis Renault (French: [lwi ʁəno]; 12 February 1877 – 24 October 1944) was a French industrialist, one of the founders of Renault, and a pioneer of the automobile industry. Renault...
2020年夏季奥林匹克运动会马来西亚代表團马来西亚国旗IOC編碼MASNOC马来西亚奥林匹克理事会網站olympic.org.my(英文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員30參賽項目10个大项旗手开幕式:李梓嘉和吳柳螢(羽毛球)[1][2]閉幕式:潘德莉拉(跳水)[3]獎牌榜排名第74 金牌 銀牌 銅�...
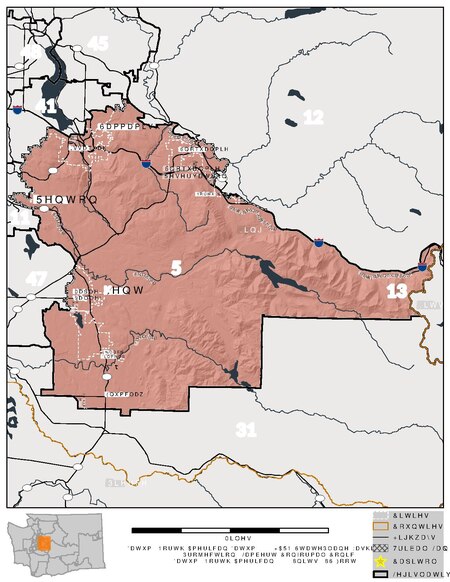
American legislative district Washington 5th legislative district map Washington's 5th legislative district is one of forty-nine districts in Washington state for representation in the state legislature. The district borders Kittitas County on the east, the 31st legislative district on the south, parts of Maple Valley, Renton, and Issaquah on the west, and Snohomish County on the north.[1] The largely rural district is represented by state senator Mark Mullet and state representatives...

British Conservative politician (born 1961) This article is about the British Conservative Party politician. For details of Ireland's former Garda Commissioner, see Martin Callinan. For the British artist, see Martin John Callanan. The Right HonourableThe Lord CallananOfficial portrait, 2018Parliamentary Under-Secretary of State for Energy Efficiency and Green FinanceIncumbentAssumed office 7 February 2023Prime MinisterRishi Sunak[1]Preceded byOffice establishedParliamentary Under...

1917 directives by Vladimir Lenin Manifestation of war veterans and invalids in Petrograd on 17 April 1917 against Lenin's arrival The April Theses (Russian: апрельские тезисы, transliteration: aprel'skie tezisy) were a series of ten directives issued by the Bolshevik leader Vladimir Lenin upon his April 1917 return to Petrograd from his exile in Switzerland via Germany and Finland. The theses were mostly aimed at fellow Bolsheviks in Russia and returning to Russia from exile....

جوزيبي سينيوري معلومات شخصية الميلاد 17 فبراير 1968 (العمر 56 سنة)ألزانو لومباردو الطول 1.70 م (5 قدم 7 بوصة) مركز اللعب مهاجم الجنسية إيطاليا مسيرة الشباب سنوات فريق 1981–1984 إنتر ميلان المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1984–1986 UC AlbinoLeffe [الإنجليزية] 38 (8) 1986�...

Krueng AcehSungai Aceh, Aceh River, Kroeeng Atjen, Krueng Atjeh, Atieh, Atye, Atjeh RivierBanjir kanal Krueng AcehLokasiNegara IndonesiaProvinsiAcehCiri-ciri fisikHulu sungaiCot Seukek, Aceh Besar[1] Muara sungaiLaut Andaman - lokasiBanda Aceh - koordinat05°35′04″N 95°18′07″E / 5.58444°N 95.30194°E / 5.58444; 95.30194Panjang145 km (90 mi)[1]Daerah Aliran SungaiSistem sungaiDAS Krueng Aceh (DAS120001)[2&...

Operating system Operating system FreeSBIEFreeSBIE 2.0 with Xfce environmentOS familyFreeBSDWorking stateUnmaintainedSource modelOpen sourceLatest release2.0.1 / February 2, 2007 (2007-02-02)Kernel typeMonolithicOfficial websitewww.freesbie.org FreeSBIE is a live CD, an operating system that is able to load directly from a bootable CD with no installation process or hard disk.[1] It is based on the FreeBSD operating system. Its name is a pun on frisbee. Currently, FreeS...

Pakubuwono IXSunan di SurakartaIn carica1861 –1893 PredecessorePakubuwono VIII SuccessorePakubuwono X NascitaSurakarta, 22 dicembre 1830 MorteSurakarta, 16 marzo 1893 (62 anni) Casa realePakubuwono PadrePakubuwono VI ReligioneIslam Pakubuwono IX, noto anche come Pakubuwana IX (Surakarta, 22 dicembre 1830 – Surakarta, 16 marzo 1893), è stato un sovrano indonesiano. Fu sunan di Surakarta dal 1861 fino alla sua morte. Indice 1 Biografia 2 Onorificenze 2.1 Onorificenze indone...

Impression couleur, de 1909, d'une aquarelle sur le couvercle d'une boîte de papeterie réalisée par Balthazar Wigand et offerte au compositeur Joseph Haydn. Il commémore la participation de Haydn à une représentation de son oratorio La Création. Un oratorio (au pluriel : oratorios, avec un « s » muet) est une œuvre lyrique dramatique représentée sans mise en scène, ni costumes, ni décors. Il peut toutefois y avoir une mise en espace. La partition est généralemen...




































