к·№н•ң
|
Read other articles:

Bergas Catursasi Penanggungan Bergas Catursasi Penanggungan (lahir 25 Juni 1975) adalah seorang birokrat Indonesia kelahiran Mojokerto.[1] Ia sempat menjabat sebagai Kepala Pelaksana Harian BPBD Jawa Tengah. Ia menjadi aparatur sipil negara yang bertugas di lingkup Pemerintah Kabupaten Kudus. Ia menjabat sebagai Kepala Pelaksana Harian BPBD Kudus. Pada 14 Januari 2022, ia dilantik menjabat sebagai pemimpin lembaga yang fokus pada penanggulangan bencana oleh Gubernur Jawa Tengah Ganjar...

Bactrocera tau Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Diptera Famili: Tephritidae Spesies: Bactrocera tau Bactrocera tau adalah spesies lalat yang tergolong famili Tephritidae. Spesies ini juga merupakan bagian dari ordo Diptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Kebanyakan anggota spesies ini bertelur dalam jaringan tumbuhan, tempat larva menemukan makanan pertamanya setelah lahir. Lalat dewasa biasanya berumur sangat pendek. Bebera...

Juru Bicara Presiden Republik IndonesiaLambang Presiden IndonesiaPetahanaLowongsejak 26 Agustus 2021Sekretariat KabinetDitunjuk olehPresiden Republik Indonesia Juru Bicara Presiden Republik Indonesia merupakan sebuah posisi dalam staf Presiden Republik Indonesia yang bertindak untuk menyampaikan komentar dan keterangan atas nama Presiden. Posisi Juru Bicara Presiden merupakan satu dari empat belas Staf Khusus Presiden yang diatur oleh Pasal 18 ayat (2) Peraturan Presiden Nomor 17 Tahun 2...

WrestleMania VLogo de WrestleMania VMain event Randy Savage contre Hulk HoganInformationsFГ©dГ©ration World Wrestling FederationDate 2 avril 1989Spectateurs 20 369[1] personnesLieu Salle de conventions Historique d'Atlantic CityVille(s) Atlantic City, New JerseyCritiquesInternet Movie Database : The Movie Database : Chronologie des Г©vГ©nementsRoyal Rumble 1989SummerSlam 1989Chronologie des WrestleManiaWrestleMania IVWrestleMania VImodifier - modifier le code - modifier Wikida...

See also: 2014 Oklahoma state elections 2014 United States House of Representatives elections in Oklahoma ← 2012 November 4, 2014 (2014-11-04) 2016 → All 5 Oklahoma seats to the United States House of Representatives Majority party Minority party Party Republican Democratic Last election 5 0 Seats won 5 0 Seat change Popular vote 457,613 174,022 Percentage 70.03% 26.63% Swing 5.41% 4.32% Election results by district Elect...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Macintosh IIcx вҖ“ news В· newspapers В· books В· scholar В· JSTOR (April 2023) (Learn how and when to remove this template message) Not to be confused with Ma...

Indian actress Rubina Ali QureshiBornRubina Ali1999 or 2000 (age 23вҖ“24)[1]Other namesRubina QureshiOccupationActressYears active2008вҖ“2013 Rubina Ali, also known as Rubina Qureshi, is an Indian actress who played the child version of Latika in the Oscar-winning film Slumdog Millionaire (2008), for which she won a Screen Actors Guild Award. Following the film's success, she was cast in the Bollywood film Kal Kisne Dekha (2009). Personal life Like her on-sc...

This is a list of Japanese snacks (гҒҠиҸ“еӯҗ, okashi) and finger foods. It includes both brand name and generic snacks. Types Anko, or sweet bean paste Anko is a kind of sweet bean paste.[1] Anko is mainly eaten during the afternoon green tea time in Japan. School students eat it after school, at home. Botamochi Daifuku Ichigodaifuku [ja] - Daifuku with strawberry Dorayaki ManjЕ« Monaka Imagawayaki Kusa mochi Taiyaki YЕҚkan Botamochi Daifuku Ichigo daifuku Dorayaki Imaga...

Marvel Comics fictional characters This article is about the Marvel Comics character. For other uses, see Plant man. Comics character PlantmanSamuel Smithers as the first Plantman.Art by Stan Woch.Publication informationPublisherMarvel ComicsFirst appearanceSamuel Smithers:Strange Tales #113 (October 1963)Paul:The Astonishing Ant-Man #7 (April 2016)Created bySamuel Smithers:Stan Lee & Joe Carter (co-writers)Dick Ayers (artist)Paul:Nick Spencer (writer)Ramon Rosanas (artist)In-story inform...

Stefano I BГЎthoryRitratto di Stefano BГЎthory attribuito a Jost Amman, 1585, Castello Reale di VarsaviaRe di PoloniaGranduca di LituaniaStemma In carica1Вә maggio 1576 вҖ“12 dicembre 1586 PredecessoreAnna SuccessoreAnna Principe di TransilvaniaIn carica1Вә maggio 1576 вҖ“12 dicembre 1586 PredecessoresГ© stesso come Voivoda di Transilvania SuccessoreSigismondo Voivoda di Transilvaniacome Stefano IXIn carica14 marzo 1571 вҖ“1Вә maggio 1576 PredecessoreGiovanni Sigismondo come Pr...
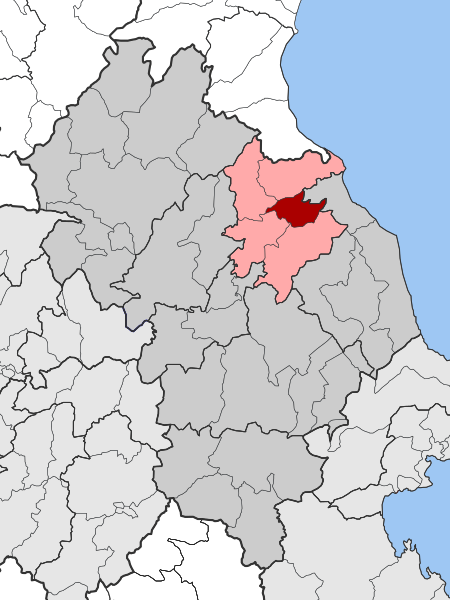
This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Ampelakia, Larissa вҖ“ news В· newspapers В· books В· scholar В· JSTOR (August 2012) (Learn how and when to remove this message) Municipal unit in GreeceAmpelakia О‘ОјПҖОөО»О¬ОәО№ОұMunicipal unitA view of AmpelakiaAmpelakiaLocation within the regional unit Coordinates: 39В°51вҖІN 22В°33вҖІE / 39....

Ne doit pas ГӘtre confondu avec Woolworth's. Cet article est une Г©bauche concernant une entreprise et lвҖҷAustralie. Vous pouvez partager vos connaissances en lвҖҷamГ©liorant (comment ?). Une page sur une entreprise Г©tant sujette Г controverse, nвҖҷoubliez pas dвҖҷindiquer dans lвҖҷarticle les critГЁres qui le rendent admissible. Woolworths Group CrГ©ation 1924 Forme juridique Public company limited by shares (d)[1] Action OTC Markets Group (WOLWF)[2] et Australian Securities Exchang...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Masashi EriguchiEriguchi pada Kejuaraan Jepang 2010Informasi pribadiKewarganegaraan JepangLahir17 December 1988 (1988-12-17) (usia 35)Kikuchi, Kumamoto, JapanAlma materUniversitas WasedaTinggi170 m (557 ft 9 in)Berat62 kg...

Irish professional golfer PГЎdraig HarringtonHarrington at the 2007 Open ChampionshipPersonal informationFull namePГЎdraig Peter HarringtonBorn (1971-08-31) 31 August 1971 (age 52)Dublin, County Dublin, Republic of IrelandHeight1.86 m (6 ft 1 in)Weight83 kg (183 lb)Sporting nationality IrelandResidenceDublin, County Dublin, Republic of IrelandSpouse Caroline (m. 1997)Children2CareerTurned professional1995Current tour(s)PGA Tour...

American comedy musician (born 1959) For the album, see Weird Al Yankovic (album). Weird Al YankovicYankovic performing in 2010Background informationBirth nameAlfred Matthew YankovicBorn (1959-10-23) October 23, 1959 (age 64)Downey, California, U.S.OriginLynwood, California, U.S.Genres Comedy parody polka geek rock[1] Occupations Singer songwriter musician record producer actor parodist author Instruments Vocals accordion keyboards DiscographyWeird Al Yankovic discographyYears ac...

President Ronald Reagan on Governors Island delivering a speech; First Lady Nancy Reagan is to the left (July 4, 1986) Liberty Weekend was a four-day celebration held to celebrate the 1984 restoration and the centenary of the Statue of Liberty (Liberty Enlightening the World) in New York City.[1] It began on July 3, 1986 and ended on July 6. July 3, 1986: opening ceremonies The Opening Ceremonies of Liberty Weekend were held on July 3, 1986 at Governors Island in New York Harbor. Fren...

Rocket engine that uses detonation waves to combust fuel and oxidizer A pulse detonation engine (PDE) is a type of propulsion system that uses detonation waves to combust the fuel and oxidizer mixture.[1][2] The engine is pulsed because the mixture must be renewed in the combustion chamber between each detonation wave and the next. Theoretically, a PDE can operate from subsonic up to a hypersonic flight speed of roughly Mach 5. An ideal PDE design can have a thermodynamic effi...

Non-material essence of a living being Not to be confused with Seoul. For other uses, see Soul (disambiguation). ArtistвҖҷs depiction of a human soul leaving the body In many religious and philosophical traditions, the soul is the non-material essence of a person, which includes one's identity, personality, and memories, an immaterial aspect or essence of a living being that is believed to be able to survive physical death. The concept of the soul is generally applied to humans, although it c...

School of DentistryTypePublic universityEstablished1945DeanDr. Andre V. RitterStudents240LocationSeattle, WA, U.S.Websitedental.washington.edu The University of Washington School of Dentistry is the dental school of the University of Washington. It is located in Seattle, and is currently the only school of dentistry in the state of Washington. The school emphasizes research in anxiety, orofacial pain, tissue repair and regeneration, immune response to bacteria, and practice based research. ...

Political party in Mexico Alliance for Yucatan Party Partido Alianza por YucatГЎnFounded1999Dissolved2010HeadquartersMexico CityIdeologyRegionalism AutonomismColoursGreenParty flagPolitics of MexicoPolitical partiesElections The Party Alliance for YucatГЎn (Spanish: Alianza Partido por YucatГЎn, PAY) was a political party in the Mexican state of YucatГЎn. It was formed in the early 21st century with the aim of representing the interests of the people of YucatГЎn at the local and national ...








































































































