ალგორითმი
|
Read other articles:

Eighth Avenue LocalServizio di trasporto pubblicoUn R160 alla stazione di Fulton StreetTipoMetropolitana Stati Stati Uniti CittàNew York Inizio168th Street FineEuclid Avenue Apertura1933 Linee impiegateEighth AvenueFulton Street GestoreMTA Mezzi utilizzatiR46 · R179 N. stazioni e fermate40 Lunghezza30.2 km Trasporto pubblico Manuale La linea C Eighth Avenue Local è una linea della metropolitana di New York, che collega la città da nord, con capolinea presso la stazio...
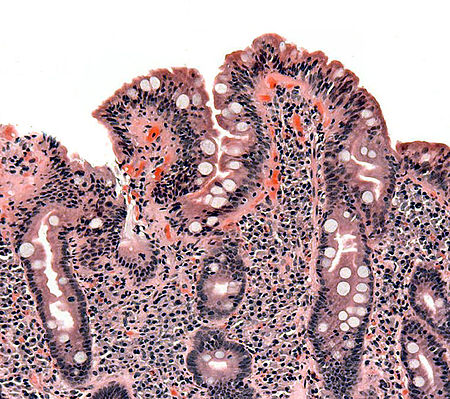
Penyakit seliakBiopsi dari usus halus yang menunjukkan penyakit seliak yang dapat dilihat dengan menumpulkan villus usus,hipertrofi crypt, dan limfosit infiltrasi cryptsInformasi umumPelafalan/ˈsiːliæk/ see-LEE-akSpesialisasiGastroenterologi, obat penyakit dalamPenyebabReaksi terhadap gluten[1]Aspek klinisGejala dan tandaTidak ada atau non-specific, distensi abdomen, diare, konstipasi, malabsorption, penurunan berat badan, dermatitis herpetiformis[2][3]KomplikasiAne...

Aidan GillenLahirAidan Murphy24 April 1968 (umur 55)Drumcondra, Dublin, IrlandiaPekerjaanAktorTahun aktif1985–sekarangSuami/istriOlivia O'Flanagan (m. 2001 - 2014)AnakBerry Murphy, Joe Murphy Aidan Gillen (/ˈɡɪlɛn/; lahir Aidan Murphy; 24 April 1968) adalah aktor Irlandia. Ia dikenal sebagai pemeran Petyr Littlefinger Baelish dalam seri produksi HBO Game of Thrones, Tommy Carcetti dalam seri The Wire, Bill Wilson di The Dark Knight Rises, Stuart Alan Jones dalam seri produksi...

Back Up!Poster gala premiereSutradaraWawan Lelono SuwantoProduserBambang ArintoDitulis oleh Wawan I. Wibowo Haikal Damara Penata musikThoersi ArgeswaraPenyuntingWawan Lelono SuwantoPerusahaanproduksi FFTV IKJ Batarini Film Post INAFEd Tanggal rilis 20 November 2019 (2019-11-20) (JAFF) 3 Mei 2020 (2020-05-03) (virtual premiere) 26 Maret 2022 (2022-03-26) (Rangkai.ID) Durasi20 menitNegaraIndonesiaBahasaIndonesia Back Up! adalah film pendek dokumenter drama Indon...

Untuk kegunaan lain, lihat Pierrot (disambiguasi). Paul Legrand berperan menjadi Pierrot pada sekitar tahun 1855. Foto buatan Nadar. Pierrot (pengucapan bahasa Prancis: [pjɛʁo]) adalah sebuah karakter stok pantonim dan Commedia dell'Arte yang bermula dari kelompok para pemain akhir abad ketujuh belas yang tampil di Paris dan dikenal sebagai Comédie-Italienne; nama tersebut adalah sebuah hipokorisme dari kata Pierre (Petrus), melalui suffix -ot. Karakternya dalam budaya populer kontemp...

German footballer (born 1967) You can help expand this article with text translated from the corresponding article in German. (December 2022) Click [show] for important translation instructions. View a machine-translated version of the German article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translat...

Defunct Washington D.C. baseball park For the concept of a sports field boundary, see Boundary (sports). Boundary FieldAmerican League Park II National ParkLocationGeorgia Avenue, 5th Street NW, W Street NW and Florida Avenue NW, Washington DCCoordinates38°55′3″N 77°1′13″W / 38.91750°N 77.02028°W / 38.91750; -77.02028OperatorNational LeagueTypeBaseball fieldSurfaceGrassConstructionDemolishedMarch 17, 1911TenantsGeorgetown Hoyas football (independent) (1891�...

Neighborhood of Chittagong, Bangladesh Faujdarhat Railway Station Faujdarhat is a neighborhood of Chittagong City in Bangladesh. It is well known as a ship breaking area, with one of the largest breaking yards in the world: Chittagong Ship Breaking Yard. There are several institutions including Faujdarhat Cadet College, the first cadet college in Bangladesh.[1] History In 1995, the Forest Department created a 5 square kilometres (1.9 sq mi) mangrove forest park that stretche...

Disambiguazione – Se stai cercando altri significati, vedi Ferrari (disambigua). Disambiguazione – Cavallino Rampante rimanda qui. Se stai cercando l'omonima pattuglia acrobatica italiana, vedi Cavallino Rampante (pattuglia acrobatica). FerrariLogo Ingresso della fabbrica Ferrari a Maranello Stato Italia Forma societariaSocietà per azioni ISINNL0011585146 Fondazione12 marzo 1947 a Maranello Fondata daEnzo Ferrari Sede principale Modena (sede legale) Maranello (sede prin...

У этого термина существуют и другие значения, см. Горностай (значения). Горностай Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстнороты...
提示:此条目页的主题不是中國—瑞士關係。 關於中華民國與「瑞」字國家的外交關係,詳見中瑞關係 (消歧義)。 中華民國—瑞士關係 中華民國 瑞士 代表機構駐瑞士台北文化經濟代表團瑞士商務辦事處代表代表 黃偉峰 大使[註 1][4]處長 陶方婭[5]Mrs. Claudia Fontana Tobiassen 中華民國—瑞士關係(德語:Schweizerische–republik china Beziehungen、法�...

Place in Świętokrzyskie Voivodeship, PolandOstrowiec ŚwiętokrzyskiCity square Coat of armsOstrowiec ŚwiętokrzyskiCoordinates: 50°56′N 21°24′E / 50.933°N 21.400°E / 50.933; 21.400Country PolandVoivodeshipŚwiętokrzyskieCountyOstrowiecGminaOstrowiec Świętokrzyski (urban gmina)City rights1613Government • City mayorArtur ŁakomiecArea • Total46.43 km2 (17.93 sq mi)Population (31 December 2021) • ...

The following is a list of major sports venues in Faisalabad, Pakistan List Stadium Capacity Game(s) City Province Tenants Image Faisalabad Hockey Stadium 25,000[1] Hockey Faisalabad Punjab Pakistan national field hockey team Iqbal Stadium 18,000[2] Cricket Faisalabad Punjab Faisalabad cricket team, Faisalabad Wolves, Pakistan national cricket team Railways Ground 5,000 Football Faisalabad Punjab Lyallpur See also List of stadiums in Pakistan List of cricket grounds in Pakist...

2014 UK local government election Map of the results The 2014 Wokingham Borough Council election took place on Thursday 22 May 2014. That was the same day as other United Kingdom local elections in order to elect members of Wokingham Unitary Council in Berkshire, England. One third of the council was up for election and the Conservative Party stayed comfortably in overall control of the council.[1] After the election, the composition of the council was: Conservative 44 Liberal Democra...
本文或本章節是關於未來的公共运输建設或計划。未有可靠来源的臆測內容可能會被移除,現時內容可能與竣工情況有所出入。 此条目讲述中国大陆處於施工或详细规划阶段的工程。设计阶段的資訊,或許与竣工后情況有所出入。无可靠来源供查证的猜测会被移除。 设想中的三条路线方案[1]。 臺灣海峽隧道或臺湾海峡橋隧(英語:Taiwan Strait Tunnel Project)是一项工程�...

Shooting Stars S.C.Calcio Oluyole Warriors Segni distintiviUniformi di gara Casa Trasferta Colori socialiBlu, bianco Dati societariCittàIbadan Nazione Nigeria ConfederazioneCAF Federazione NFA CampionatoNigeria Premier League Fondazione1950 StadioStadio Adamasingba(10 000 posti) PalmarèsTitoli nazionali5 Campionati nigeriani Trofei nazionali3 Coppe di Nigeria Trofei internazionali1 Coppe CAF1 Coppe delle Coppe d'Africa Si invita a seguire il modello di voce LoShooting Stars S.C., megli...

Ketch The Gipsy Moth IV on display in Greenwich, England. History United Kingdom NameGipsy Moth IV OwnerFrancis Chichester LaunchedMarch 1966 In service27 August 1966 StatusIn active service with the Royal Thames Yacht Club NotesRestored in 2004 and 2022 General characteristics Sail planKetch Gipsy Moth IV is a 53 ft (16 m) ketch that Sir Francis Chichester commissioned specifically to sail single-handed around the globe, racing against the times set by the clipper ships of the 19th...

Grand Prix Brasil 2008 Lomba ke-18 dari 18 dalam Formula Satu musim 2008← Lomba sebelumnyaLomba berikutnya → Detail perlombaan[1][2]Tanggal 02 November 2008 (2008-11-02)Nama resmi Formula 1 Grande Prêmio do Brasil 2008Lokasi Autódromo José Carlos Pace, São Paulo, BrazilSirkuit Fasilitas balap permanenPanjang sirkuit 4.309 km (2.677 mi)Jarak tempuh 71 putaran, 305.909 km (190.083 mi)Cuaca Hujan di awal dan akhir, dalam keadaan lain keringPosisi ...

كنيسة المشرق كنيسة القديسة مريم المشرقية الآشورية في أرومية بإيران: بُنيت في القرن السابعكنيسة القديسة مريم المشرقية الآشورية في أرومية بإيران: بُنيت في القرن السابع العائلة الدينية مسيحية شرقية (مسيحية سريانية) الإسم باللغة الأصلية (بالسريانية: ܥܕܬܐ ܕܡܕܢܚܐ) الإيمان ديو�...

Sculpture by James Paxton Voorhees Daniel W. VoorheesArtistJames P. VoorheesYearc1905-1909 (c1905-1909)TypePlaster bustDimensions46 cm × 69 cm × 79 cm (18 in × 27 in × 31 in)LocationIndiana Statehouse, IndianapolisCoordinates39°46′8.4″N 86°9′46.8″W / 39.769000°N 86.163000°W / 39.769000; -86.163000OwnerState of Indiana Daniel W. Voorhees is a public artwork by American artist Jame...









