静水圧平衡
|
Read other articles:

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Kompos – berita · surat kabar · buku · cendekiawan · JSTOR (Februari 2014) Kompos dari sampah dedaunan Kompos dari jerami padi Kompos adalah hasil penguraian parsial/tidak lengkap dari campuran bahan-bahan or...

2024 في التقاويم الأخرىتقويم ميلادي2024MMXXIVتقويم هجري1445–1446تقويم هجري شمسي1402–1403تقويم أمازيغي2974من بداية روما2777تقويم أرمني1473ԹՎ ՌՆՀԳتقويم سرياني6774تقويم بهائي180–181تقويم بنغالي1431 سنة عرش بريطاني2 تشارلز. 3 – 3 تشارلز. 3تقويم بوذي2568تقويم بورمي1386تقويم بيزنطي7532–7...

Cet article possède des paronymes, voir Antoine Alexis Perier de Salvert, Antoine-Hilaire-Henri Périé et Perrier (acteur). Pour les articles homonymes, voir Perrier. Antoine Perrier Antoine Perrier à l'enterrement de Maurice Berteaux en mai 1911. Fonctions Vice-président du Sénat 1910 – 1914(4 ans) Sénateur de la Savoie 28 janvier 1900 – 7 avril 1914(14 ans, 2 mois et 10 jours) Garde des Sceaux, ministre de la Justice 2 mars 1911 – 23 juin 1911(3 mois et...

Keisuke Saka Keisuke Saka, pemain sepak bola Jepang yang datang ke Taiwan untuk mengikuti pertandingan sepak bola Summer World University Games 2017Informasi pribadiNama lengkap Keisuke SakaTanggal lahir 7 Mei 1995 (umur 28)Tempat lahir Prefektur Mie, JepangPosisi bermain BekInformasi klubKlub saat ini Shonan BellmareKarier senior*Tahun Tim Tampil (Gol)2018– Shonan Bellmare * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Keisuke Saka (lahir 7 Mei 1995) adalah pem...
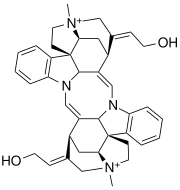
Chemical compound ToxiferineIdentifiersCAS Number302-30-7PubChem CID5281411ChemSpider4444760UNII9M7D9K3OJIChEMBLChEMBL231047CompTox Dashboard (EPA)DTXSID30897243 Chemical and physical dataFormulaC40H46N4O2Molar mass614.834 g·mol−13D model (JSmol)Interactive image SMILES [H][C@@]12[C@@]3(CC[N+]2(C)C/C4=C/CO)[C@@]5([H])N(C6=C3C=CC=C6)/C=C7[C@]([C@@]8(CC[N+]9(C)C/%10)[C@]9([H])C[C@]\7([H])C%10=C/CO)([H])N(C%11=C8C=CC=C%11)/C=C5/[C@]4([H])C1 Toxiferine (C-toxiferine I) is a curare toxin. ...

Франц Саксен-Кобург-Заальфельдскийнем. Franz von Sachsen-Coburg-Saalfeld герцог Саксен-Кобург-Заальфельдский 8 сентября 1800 — 9 декабря 1806 Предшественник Эрнст Фридрих Саксен-Кобург-Заальфельдский Преемник Эрнст I Саксен-Кобург-Заальфельдский Рождение 15 июля 1750(1750-07-15)Кобург, Сакс...

American radio personality Phil HendrieBornArcadia, California, U.S.OccupationsRadio personalityactorentrepreneurYears active1973–presentKnown forRadio satireNotable workThe Phil Hendrie ShowWebsitephilhendrieshow.com Philip Stephen Hendrie is an American radio personality and actor.[1][2] He is widely known for his voiceover talent throughout the radio and film industry.[3] He came to prominence in the 1990s hosting The Phil Hendrie Show, a radio talk show...

Dieser Artikel oder nachfolgende Abschnitt ist nicht hinreichend mit Belegen (beispielsweise Einzelnachweisen) ausgestattet. Angaben ohne ausreichenden Beleg könnten demnächst entfernt werden. Bitte hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Emanuel Haldeman-Julius Emanuel Haldeman-Julius (* 30. Juli 1889 in Philadelphia, Pennsylvania; † 31. Juli 1951), geboren als Emanuel Julius, war ein sozialistischer Reformer und Verleger jüdischer Abstammung. Sech...

Measurement of the human penis Penis length and Small penis redirect here. For differences in penis length among non-human species, see Penis § In different animals. For the medical term, see Micropenis. Big dick redirects here. For other uses, see Big Dick (disambiguation). Diagram showing how to measure the length and circumference of an erect human penis Human penises vary in size on a number of measures, including length and circumference when flaccid and erect. Besides the natural ...

Halaman ini berisi artikel tentang geografi Persemakmuran Australia. Untuk perlakuan benua, lihat Australia (benua). Untuk daratan utama, lihat Daratan utama Australia. 27°S 144°E / 27°S 144°E / -27; 144 Geografi Australia BenuaAustraliaKawasanOseaniaKoordinat27°00′00″S 144°00′00″E / 27.000°S 144.000°E / -27.000; 144.000WilayahPeringkat ke-67,686,850 km² (Kesalahan ekspresi: Karakter tanda baca "," tidak dikenal.&...
Copa di Israele 1961-1962Dettagli della competizioneSport Pallacanestro Federazione IBBA Periodo1961 —14 agosto 1962 LuogoHolon ImpiantoHolon Basketball Stadium VerdettiCampione Hapoel Tel Aviv(1º titolo) Cronologia della competizioneed. successiva → ← ed. precedente Modifica dati su Wikidata · Manuale La Coppa di Israele 1961-1962 è la 5ª Coppa di Israele di pallacanestro maschile.La finale della competizione si è disputata alla Holon Bask...

6º torneo olimpico di calcioParigi 1924Informazioni generaliSport Calcio EdizioneGiochi della VIII Olimpiade Paese ospitante Francia CittàParigi Periododal 25 maggio 1924 al 9 giugno 1924 Nazionali 23 (22 effettive) Incontri disputati24 Gol segnati96 (4 per partita) Classifica finale Vincitore Uruguay (1º titolo) Secondo Svizzera Terzo Svezia Cronologia della competizione Anversa 1920 Amsterdam 1928 Voce principale: Giochi della VIII Olimpiade. Il torneo di calci...

Premier League Malti 1926-1927 Competizione Premier League Malti Sport Calcio Edizione 16ª Organizzatore MFA Luogo Malta Partecipanti 4 Formula 1 girone all'italiana Risultati Vincitore Floriana(7º titolo) Statistiche Incontri disputati 12 Gol segnati 8 (0,67 per incontro) Cronologia della competizione 1925-26 1927-28 Manuale Il campionato era formato da sole quattro squadre e il Floriana vinse il titolo. Classifica finale Pos. Squadra G V N P GF GS Punti 1 Floriana 3 2 1 ...

Mathematical description of quantum state Not to be confused with Wave equation. Comparison of classical and quantum harmonic oscillator conceptions for a single spinless particle. The two processes differ greatly. The classical process (A–B) is represented as the motion of a particle along a trajectory. The quantum process (C–H) has no such trajectory. Rather, it is represented as a wave; here, the vertical axis shows the real part (blue) and imaginary part (red) of the wave function. Pa...

凡例山名 時氏 『本朝百将伝』より時代 鎌倉時代末期 - 南北朝時代生誕 嘉元元年(1303年)別説では永仁6年(1298年)死没 建徳2年/応安4年3月28日(1371年4月14日)[1]別名 小次郎戒名 光孝寺殿鎮国道静大禅定門[1]墓所 鳥取県倉吉市の山名寺官位 正五位下伊豆守、弾正少弼、左京大夫[1]幕府 室町幕府 侍所頭人、引付頭人、伯耆・出雲・隠岐・因幡・�...

香港トラム 第4世代のNo. 50第4世代のNo. 50 堅尼地城總站 石塘咀總站 屈地街電車廠 港澳碼頭 上環(西港城)總站 上環 MTR港島線乗換 香港 轉乘港鐵 中環 MTR荃湾線・港島線乗換 中環碼頭 金鐘 MTR荃湾線・港島線乗換 湾仔 MTR港島線乗換 跑馬地總站 銅鑼湾 MTR港島線乗換 銅鑼湾總站 天后 MTR港島線乗換 炮台山 MTR港島線乗換 北角總站 北角 MTR港島線・将軍澳線乗換 北角碼頭 �...

Act of killing one's own brother For other uses, see Fratricide (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fratricide – news · newspapers · books · scholar · JSTOR (June 2008) (Learn how and when to remove this message) Cain kills Abel, a fratricide illustrated by Gustave Doré (And Ca...

The Cologne Progressives was an art movement and were an informal group of artists based in the Cologne and Düsseldorf area of Germany. They came together following the First World War and participated in the radical workers' movement. History Heinrich Hoerle, Monument to the Unknown Protheses (1930) The group was founded by Gerd Arntz, Heinrich Hoerle and Franz Wilhelm Seiwert.[1] The group related their attitude to art to their political activism. As Wieland Schmied put it, they so...

Les ESPY Awards sont un événement sportif, télévisuel et annuel qui a été créé en 1993 par le réseau de chaînes et radio sportifs Entertainment and Sports Programming Network (ESPN). « ESPY » est un acronyme signifiant Excellence in Sports Performance Yearly (Excellence annuelle dans les performances sportives). ESPN est depuis sa création en 1979 une référence en matière sportive. Les ESPY Awards pourraient être comparés dans une autre mesure mais en restant dans...

Nota: Para outros significados, veja Roma (desambiguação). Roma Capital da Itália Panorama urbano visto do Castelo de Santo ÂngeloFontana di TreviColiseuBarcaccia e Trinità dei MontiBasílica de São PedroCastelo de Santo ÂngeloPanteão e Piazza della RotondaMonumento a Vítor Emanuel II Símbolos Bandeira Brasão de armas Gentílico romano Localização Roma Mapa de Roma Coordenadas 41° 53′ 36″ N, 12° 28′ 58″ L País Itália Região metropolitan...












