ルーティングテーブル
|
Read other articles:

2010 single by MonroseLike a LadySingle by Monrosefrom the album Ladylike Released28 May 2010Length3:09LabelStarwatchCheyenneWarnerSongwriter(s)Risto AsikainenZippy DavisVeikka ErcolaAlexander KomlewProducer(s)TuneverseMonrose singles chronology Why Not Us (2008) Like a Lady (2010) This Is Me (2010) Like a Lady is a song performed by German girl band Monrose. It was written by Risto Asikainen, Zippy Davis, Veikka DJ Ercola Erkola and Alexander Komlew and recorded for their fourth studio album...
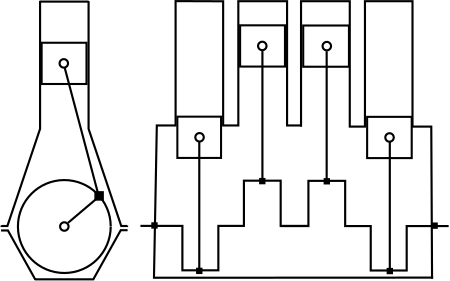
Skema sebuah mesin 4 silinder-segaris Dalam konfigurasi sebuah mesin, mesin segaris adalah sebuah mesin pembakaran dalam yang semua silindernya terletak segaris. Mesin seperti ini sudah banyak digunakan di dunia otomotif, penerbangan, dan lokomotif. Mesin segaris lebih mudah dibuat dari mesin jenis lainnya, seperti mesin flat atau mesin V karena hanya membutuhkan satu cabang silinder dan crankshaft. Mesin ini juga membutuhkan cylinder head dan camshaft yang lebih sedikit. Penggunaan oleh pabr...

Strada statale 506della Valle d'AyasDenominazioni successiveStrada regionale 45 della Valle d'Ayas LocalizzazioneStato Italia Regioni Valle d'Aosta DatiClassificazioneStrada statale InizioVerrès FineSaint-Jacques d'Ayas Lunghezza30,982[1] km Provvedimento di istituzioneD.M. 5/08/1966 - G.U. 242 del 28/09/1966[2] GestoreTratte ANAS: nessuna (dal 1994 la gestione è passata alla Regione Valle d'Aosta) Manuale La ex strada statale 506 della Valle d'Ayas (SS 506), ora s...

Drain line redirects here. For the London Underground line, nicknamed The Drain, see Waterloo & City line. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Condensate pump – news · newspapers · books · scholar · JSTOR (June 2022) (Learn how and when to remove this template message) Air condensate pump. No...

Painting by Pablo Picasso Brick Factory at TortosaArtistPablo PicassoYear1909MediumOil on canvasMovementProto-CubismDimensions50.7 cm × 60.2 cm (20.0 in × 23.7 in)LocationThe State Hermitage Museum, Saint Petersburg, Russia Brick Factory at Tortosa (L'Usine, Horta de Ebro) is a 1909 oil on canvas painting by Pablo Picasso, which he created during a visit to Horta de Sant Joan in Catalonia. It depicts a landscape of a factory and palm trees, which ar...

Swiss author and founder of a UFO religion Billy MeierBornEduard Albert Meier (1937-02-03) 3 February 1937 (age 87)[1]Bülach/ZH, SwitzerlandNationalitySwissOccupation(s)Author, ufologistOrganization(s)Freie Interessengemeinschaft für Grenz- und Geisteswissenschaften und Ufologiestudien (Free Community of Interests for the Border and Spiritual Sciences and Ufological Studies) (FIGU)Known forContactee/UFO religionChildren4ParentJulius Meier Websitewww.figu.org Eduard Albert ...

非常尊敬的讓·克雷蒂安Jean ChrétienPC OM CC KC 加拿大第20任總理任期1993年11月4日—2003年12月12日君主伊利沙伯二世总督Ray HnatyshynRoméo LeBlancAdrienne Clarkson副职Sheila Copps赫布·格雷John Manley前任金·坎貝爾继任保羅·馬田加拿大自由黨黨魁任期1990年6月23日—2003年11月14日前任約翰·特納继任保羅·馬田 高級政治職位 加拿大官方反對黨領袖任期1990年12月21日—1993年11月...

Diagram of font metrics showing where letters and symbols would be placed relative to each other. The letters would change size according to the font type, typographic unit and dimension used. Metric typographic units have been devised and proposed several times to overcome the various traditional point systems. After the French Revolution of 1789 one popular proponent of a switch to metric was Didot, who had been able to standardise the continental European typographic measurement a few deca...

ESPN's main studio show for its coverage of the National Hockey League The PointGenreNHLPresented byJohn BuccigrossTheme music composerBob ChristiansonCountry of originUnited StatesOriginal languageEnglishProductionProduction location Bristol, CT studios (most segments) Camera setupMulti-cameraRunning time1 hourProduction companyESPNOriginal releaseNetwork ESPN2 ESPN+ ESPN[a] ReleaseOctober 7, 2021 (2021-10-07) –presentRelated NHL on ESPN NHL on ABC NHL 2Night The Point is...

اقتصاد الأرجنتينعامالدولة الأرجنتين عملة بيزو أرجنتيني الإحصائياتالناتج الإجمالي 631.133 بليون دولار أمريكي[1](2022) نمو الناتج الإجمالي -2.3 نسبة مئوية[2](2016) نصيب الفرد من الناتج الإجمالي 14398 دولار أمريكي[3](2017) المالية العامةإجمالي الاحتياطي 55.314 بليون دولار أمريكي&#...

American state election 2006 Michigan Secretary of State election ← 2002 November 7, 2006 2010 → Nominee Terri Lynn Land Carmella Sabaugh Party Republican Democratic Popular vote 2,089,864 1,561,828 Percentage 56.15% 41.96% County results Precinct resultsLand: 40–50% 50–60% 60–70% 70–80% 80–90% &...

2014 Chinese film12 Citizens十二公民Directed byXu Ang (徐昂)Written byJinglong Han (韩景龙)Yujiao Li (李玉娇)Based onTwelve Angry Menby Reginald RoseProduced byYan Jianwei (严建伟)Liangwen Li (李良文)Yang Ming (杨明)Luna Wang (王露娜)CinematographyTao Cai (陶彩)Edited byWang Gang (王刚)Jiale Yin (尹佳乐)Music byRadio MarsRelease dates October 19, 2014 (2014-10-19) (Rome) May 15, 2015 (2015-05-15) (China) Running time106 minut...

«Письма римскому другу (Из Марциала)»[1] — стихотворение (публикуемое также как поэтический цикл) Иосифа Бродского, написанное в марте 1972 года — за три месяца до отъезда из СССР[2]. Исследователями творчества Бродского рассматривается как программный манифест по�...

1967 amendment enumerating presidential succession Twenty-fifth Amendment redirects here. For other uses, see Twenty-fifth Amendment (disambiguation). This article is part of a series on theConstitutionof the United States Preamble and Articles Preamble I II III IV V VI VII Amendments to the Constitution I II III IV V VI VII VIII IX X XI XII XIII XIV XV XVI XVII XVIII XIX XX XXI XXII XXIII XXIV XXV XXVI XXVII Unratified Amendments: Congressional Apportionment Titles of Nobility Corwin Child L...

Set of economic theories and practices within anarchism Part of a series onAnarchism History Outline Schools of thought Feminist Green Primitivist Social ecology Total liberation Individualist Egoist Free-market Naturist Philosophical Mutualism Postcolonial African Black Queer Religious Christian Jewish Social Collectivist Parecon Communist Magonism Without adjectives Methodology Agorism Illegalism Insurrectionary Communization Expropriative Pacifist Platformism Especifismo Relationship Syndi...

العلاقات الأرجنتينية النيوزيلندية الأرجنتين نيوزيلندا الأرجنتين نيوزيلندا تعديل مصدري - تعديل العلاقات الأرجنتينية النيوزيلندية هي العلاقات الثنائية التي تجمع بين الأرجنتين ونيوزيلندا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Cultural depictions of Ronald Reagan – news · newspapers · books · scholar · JSTOR (August 2016) (Learn how and when to remove this message) This article is part of a series aboutRonald Reagan Personal life Filmography Bibliography Death Residences Birthplace o...

Ini adalah nama Korea; marganya adalah Kim. Kim Chan-miChanmi, Januari 2018Nama asal김찬미LahirKim Chan-mi19 Juni 1996 (umur 28)Gumi, Gyeongsang Utara, Korea SelatanPendidikanSekolah Menengah Atas Youngdeungpo[1]Pekerjaanpenyanyi, rapperTinggi166 cm (5 ft 5 in) (2015)[2]Berat47 kg (104 pon) (104 pon) (2015)[2]Karier musikGenreMusik populer, K-PopTahun aktif2012–sekarangLabelFNC EntertainmentArtis terkaitAOA, AOA WhiteSitus webhtt...

Cet article est une ébauche concernant le Kansas. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir Jackson et Comté de Jackson. Comté de Jackson( Jackson County) State Bank de Holton (2014) Administration Pays États-Unis État Kansas Chef-lieu Holton Fondation 1859 Démographie Population 13 500 hab. (2006) Densité 8 hab./km2 Géographie Coordonnées 39° ...

Three linked but pairwise separated rings Borromean ringsL6a4Crossing no.6Hyperbolic volume7.327724753Stick no.9Conway notation.1A–B notation632ThistlethwaiteL6a4Otheralternating, hyperbolic In mathematics, the Borromean rings[a] are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these...