チューリングマシン
|
Read other articles:

American film director Lambert HillyerBornLambert Harwood Hillyer(1893-07-08)July 8, 1893Tyner, IndianaDiedJuly 5, 1969(1969-07-05) (aged 75)Los Angeles, CaliforniaOccupation(s)Film director, screenwriterYears active1917–1949 Lambert Harwood Hillyer (July 8, 1893 – July 5, 1969) was an American film director and screenwriter. Biography Lambert Harwood Hillyer was born July 8, 1893, in Tyner, Indiana.[1] His mother was character actress Lydia Knott.[2] A gradu...

Beautiful WorldAlbum studio karya ArashiDirilis06 Juli 2011 (2011-07-06)Direkam2010-2011GenrePop, R&BDurasi75:31[1]LabelJ StormKronologi Arashi Boku no Miteiru Fūkei(2010)String Module Error: Match not found2010 Beautiful World(2011) Ura Ara Mania(2012)String Module Error: Match not found2012 Singel dalam album Beautiful World To Be FreeDirilis: 07 Juli 2010 (2010-07-07) Love RainbowDirilis: 08 September 2010 (2010-09-08) Dear SnowDirilis: 21 Oktober 2010 ...

Village in Narragansett, Rhode Island, US Skips Dock Jerusalem is a fishing village within the town of Narragansett, Rhode Island, on Point Judith. It is across the harbor from Galilee, Rhode Island. It is named after the Biblical city of Jerusalem. Jerusalem is not attached to any other part of Narragansett by land; its only land border is with the Matunuck section of South Kingstown, Rhode Island. Although Jerusalem is not in the Town of South Kingstown, fire and police service in Jerusalem...

Nama ini menggunakan cara penamaan Portugis. Nama keluarga pertama atau maternalnya adalah Luiz dan nama keluarga kedua atau paternalnya adalah da Silva. Cristian Alberto bin Danilo Luiz Roza da Silva Informasi pribadiNama lengkap Cristian Alberto bin Danilo Luiz Roza da Silva [1]Tanggal lahir 15 Juli 1991 (umur 32)[2]Tempat lahir Bicas, BrasilTinggi 184 cm (6 ft 0 in)[3]Posisi bermain Bek sisiInformasi klubKlub saat ini JuventusNomor 6Karier ju...

Dalam nama Korea ini, nama keluarganya adalah Ho. Ho Hon허헌Hŏ HŏnHon KetuaMajelis Rakyat TertinggiMasa jabatan ke-1Masa jabatan10 September 1948 – 16 Agustus 1951Wakil Ketua 2 menjabat Kim Tal-hyon Yi Yong Perdana MenteriKim Il-sungPendahuluJabatan dibentukPenggantiYi YongKetuaPartai Buruh Korea Selatanmas ajabatan ke-1Masa jabatan24 November 1946 – 24 Juni 1949Wakil Ketua 2 menjabat Pak Hon-yong Yi Ki-sok PendahuluPak Hon-yongPenggantiKim Il-sungPerdana M...

Orang BulgariaБългариKrum · John dari Rila · Ivan Alexander · Vasil Levski · Hristo Botev Stefan Stambolov · Christo · Elena Yoncheva · Ludmilla Diakovska · Matey KaziyskiDaerah dengan populasi signifikan Bulgaria6.655.210[1] Makedonia Utara1.300.000[2] Ukraina204.600[3] Spanyol154.000[4] Amerika Serikat92.841 - 300.000[5] [6]&...

2003 studio album by Benny BenassiHypnoticaStudio album by Benny BenassiReleased19 August 2003GenreElectro houseLength61:27LabelUltraDataMinistry of SoundEnergyZYXProducerLarry PignagnoliBenny Benassi chronology Hypnotica(2003) Rock 'n' Rave(2008) Professional ratingsReview scoresSourceRatingAbout.com link Hypnotica is the debut studio album by Italian DJ and producer Benny Benassi which was released in 2003. The band was titled as Benny Benassi Presents the Biz, where the Biz are the...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Village in FloridaRoyal Palm Beach, FloridaVillageVillage of Royal Palm BeachLocation of Royal Palm Beach in Palm Beach County, FloridaCoordinates: 26°42′21″N 80°13′36″W / 26.70583°N 80.22667°W / 26.70583; -80.22667Country United States of AmericaState FloridaCounty Palm BeachIncorporatedJune 18, 1959Government • TypeMayor-Council • MayorFred Pinto (D)[1][2] • Vice MayorJeff Hmara • ...

ورد الغراممعلومات عامةتاريخ الصدور 10 ديسمبر 1951مدة العرض 120 دقيقةاللغة الأصلية العربيةالعرض أبيض وأسود البلد مصرالطاقمالمخرج هنري بركاتالكاتب يوسف عيسى (قصة)هنري بركات (سيناريو) بديع خيري (حوار)البطولة محمد فوزيليلى مرادسليمان نجيبسراج منيرالتصوير وحيد فريدالموسيقى �...

عادل العزازي معلومات شخصية الميلاد سنة 1958 (العمر 65–66 سنة) مواطنة مصر الحياة العملية أعمال بارزة معرفة الصحابة (دار الوطن، 1419هـ) [لغات أخرى] تعديل مصدري - تعديل عادل يوسف العزازي (ولد عام 1958) هو شيخ سلفي مصري يُكنى بأبو عبد الرحمن. نجح في انتخابات مجلس...

حزب اليسار الراديكالي البلد فرنسا التأسيس تاريخ التأسيس 1972 الشخصيات الرئيس غيوم لاكروا عدد الأعضاء 3500 (2022) المقر الرئيسي باريس الأفكار الأيديولوجيا راديكالية علمانية فدرلة الاتحاد الأوروبي جمهوريانية ليبرالية اجتماعية الانحياز السياسي وسط اليسار انتساب د...
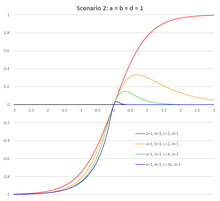
Mathematical activation function in data analysis The Soboleva modified hyperbolic tangent, also known as (parametric) Soboleva modified hyperbolic tangent activation function ([P]SMHTAF),[nb 1] is a special S-shaped function based on the hyperbolic tangent, given by Equation Left tail control Right tail control smht x = e a x − e − b x e c x + e − d x . {\displaystyle \operatorname {smht} x={\frac {e^{ax}-e^{-bx}}{e^{cx}+e^{-dx}}}.} History This function...
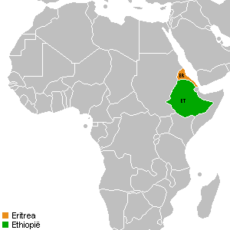
Resolusi 1434Dewan Keamanan PBBEritrea (jingga) dan Ethiopia (hijau)Tanggal6 September 2002Sidang no.4.606KodeS/RES/1434 (Dokumen)TopikSituasi antara Eritrea dan EthiopiaRingkasan hasil15 mendukungTidak ada menentangTidak ada abstainHasilDiadopsiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Rusia Britania Raya Amerika SerikatAnggota tidak tetap Bulgaria Kamerun Kolombia Guinea Irlandia Meksiko Mauritius Norweg...

Pour les articles homonymes, voir Avtsine et Aveline. Claude AvelineClaude Aveline en 1989 au vernissage d'une exposition de Hamid TibouchiBiographieNaissance 19 juillet 19015e arrondissement de Paris (France)Décès 4 novembre 1992 (à 91 ans)15e arrondissement de Paris (France)Nom de naissance Eugène Avtsine, devenu officiellement Aveline (1951), Claude (1956)Surnom Louis-Marie Martin dans la Résistance (1943), Denis (Les Cahiers de Libération, 1943) Minervois (Éditions ...

テレビ番組・中継内での各種情報(終了した番組・中継を含みます)は、DVDやBlu-rayなどでの販売や公式なネット配信、または信頼できる紙媒体またはウェブ媒体が紹介するまで、出典として用いないで下さい。 検証可能性に基づき除去される場合があります。 ラジオ番組・中継内での各種情報(終了した番組・中継を含みます)は、CDなどでの販売や公式なアーカイブ...

Prime Minister of the United Kingdom from 1957 to 1963 The Right HonourableThe Earl of StocktonOM PC FRSMacmillan in 1959Prime Minister of the United KingdomIn office10 January 1957 – 18 October 1963MonarchElizabeth IIFirst SecretaryRab Butler (1962–63)Preceded byAnthony EdenSucceeded byAlec Douglas-HomeLeader of the Conservative PartyIn office10 January 1957 – 18 October 1963Preceded byAnthony EdenSucceeded byAlec Douglas-Home Ministerial offices Chancellor of...

Major branch of Buddhism Part of a series onTheravāda Buddhism Countries Bangladesh Cambodia China India Laos Myanmar Nepal Sri Lanka Thailand Vietnam Western world Texts Pāli Tipiṭaka Paracanonical texts Commentaries Sub-commentaries Vimuttimagga Visuddhimagga Abhidhammavatara Abhidhammattha-sangaha Yogāvacara's manual History Pre-sectarian Buddhism Early schools Sthaviras Buddhist councils Vibhajjavada Mahāvihāra Dipavamsa Mahavamsa Pali Text Society Schools Buddhist modernism Vipass...

For other uses, see Wroughton (disambiguation). Human settlement in EnglandWroughtonOpen space near the main road through WroughtonWroughtonLocation within WiltshirePopulation8,239 (in 2021)[1]OS grid referenceSU150819Civil parishWroughtonUnitary authoritySwindonCeremonial countyWiltshireRegionSouth WestCountryEnglandSovereign stateUnited KingdomPost townSWINDONPostcode districtSN4Dialling code01793PoliceWiltshireFireDorset and WiltshireAmbulanc...

Israeli footballer (born 1992) Niv Antman Personal informationFull name Niv AntmanDate of birth (1992-08-02) 2 August 1992 (age 32)Place of birth Haifa, IsraelPosition(s) GoalkeeperTeam informationCurrent team Hapoel HaifaNumber 13Youth career2003–2006 Maccabi Tzur Shalom2006–2008 Maccabi Haifa2008–2012 Hapoel HaifaSenior career*Years Team Apps (Gls)2012–2016 Hapoel Haifa 19 (0)2016 Hapoel Rishon LeZion 1 (0)2016–2017 FC Dordrecht 1 (0)2017–2018 Ironi Nesher 23 (0)2018–2021...






















