CHARMING (スターダストレビューのアルバム)

『LOVE SONGS』
スターダストレビュー の カバー・アルバム
リリース
ジャンル アカペラ
ポップス
時間
レーベル ワーナーミュージック・ジャパン
スターダストレビュー アルバム 年表
VOICE
（1986年）		CHARMING
（1986年）		NIGHT SONGS
（1987年）
テンプレートを表示

『CHARMING』（チャーミング）はスターダストレビュー1枚目のアカペラ・アルバム。1986年12月10日に発売された。[1][2]

収録曲

全曲　編曲：三谷泰弘

  1. Charming　（作詞・作曲：三谷泰弘）
  2. 踊りあかそう　（I Could Have Danced All Night）
    （作詞：Alan Jay Lerner　作曲：Frederick Loewe）
  3. 星に願いを　（When You Wish Upon A Star）
    （作詞：Ned Washington　作曲：Leigh Harline）
  4. 上を向いて歩こう　（作詞：永六輔　作曲：中村八大）
  5. Lazy Afternoon　（作詞：根本要/林紀勝　作曲：三谷泰弘）
  6. Sweet Memories　（作詞：松本隆　作曲：大村雅朗）
  7. 雨に歌えば　（Singin' In The Rain）
    （作詞：Nacio Herb Brown　作曲：Arthur Freed）
  8. Goodnight　（作詞・作曲：三谷泰弘）

脚注

[脚注の使い方]
  1. ^ “スターダスト☆レビュー/CHARMING”. tower.jp. 2021年11月4日閲覧。
  2. ^ “CHARMING”. スターダスト☆レビュー オフィシャルサイト. 2021年11月4日閲覧。

関連項目

根本要 (ギター・ボーカル) - 柿沼清史 (ベース・ボーカル) - 寺田正美 (ドラムス・ボーカル) - 林“VOH”紀勝 (パーカッション・ボーカル)
三谷泰弘 (キーボード) - 光田健一 (キーボード)
シングル

1.シュガーはお年頃 - 2.銀座ネオン・パラダイス - 3.ブラックペッパーのたっぷりきいた私の作ったオニオンスライス - 4.トワイライト・アヴェニュー - 5.夢伝説 - 6.想い出にかわるまで - 7.Single Night - 8.6月のジングル・ベル - 9.今夜だけきっと - 10.もう一度ハーバーライト - 11.心の中のFollow Wind - 12.One More Time - 13.メビウスの瞳 - 14.Stay My Blue - 君が恋しくて - - 15.Northern Lights -輝く君に- - 16.夏のシルエット - 17.Be My Lady - 18.Lonely Snow Bird - 19.君のキャトル・ヴァン・ディス - 20.君のすべてが悲しい - 21.こしゃくなレディ - 22.瞳の中の天国 - 23.追憶 - 24.もう一度抱きしめて - 25.木蘭の涙 - 26.クレイジー・ラブ - 27.ふたり - 28.会えないよ - 29.Get Up My Soul - 30.もうチョットだけ何か足りない - 31.愛してるの続き - 32.何やってんだろう - 33.7月7日 - 34.ワイン恋物語 - 35.どうして - 36.今夜だけきっと/ナチュラル〜抱きしめてこのままで〜 - 37.What is Love? - 38.My Love - 39.Joanna - 40.My pride,your pride/Step by step - 41.デェラ・シエラ・ム (CHAGE and ASKA + Stardust Revue) - 42.本日のスープ (大泉洋 with STARDUST REVUE) - 43.Find My Way - 44.南風吹く丘で - 45.木蘭の涙〜acoustic〜 - 46.いのちのこたえ - 47.WAKE UP! MY HEART - 48.愛の歌 - 49.夢伝説 - 50.潮騒静夜 - 51.夢への地図 - 52.Magic 〜手をつなごう〜 - 53.今日もいい日でありますように - 54.Crying - 55.おぼろづき - 56.世界はいつも夜明け前 - 57.うしみつジャンボリー - （配信）ちょうどいい幸せ - （配信）偶然の再会 - 58.はっきりしようぜ - （配信）やっぱり会いたいよ

アルバム
オリジナル
ベスト
ライブ
アカペラ

1.CHAMING - 2.DEVOTION - 3.ALWAYS

関連項目
スタブアイコン

この項目は、アルバムに関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（P:音楽/PJアルバム）。

Read other articles:

Penapisan (kedokteran)

Seorang penambang batu bara menyelesaikan tinjauan penyaringan untuk paru-paru hitam. Dalam kedokteran, penapisan atau penyaringan (Inggris: screeningcode: en is deprecated ) adalah cara yang digunakan untuk mencari keadaan atau penanda risiko yang belum diketahui.[1][2][3] Pengujian ini dapat diterapkan kepada individu atau seluruh populasi. Orang yang diuji mungkin tidak menunjukkan tanda atau gejala penyakit apa pun atau menunjukkan satu atau dua gejala yang dengan ...

 

Andanada

Restaurant in New York, United StatesAndanadaRestaurant informationEstablished2012Closed2017Head chefManuel BerganzaFood typeSpanishCityNew York CityStateNew YorkCountryUnited States Location had a different restaurant in 2020 Andanada was a Spanish restaurant located at 141 West 69th Street (between Broadway and Columbus) on the Upper West Side in Manhattan, New York City. Opening in 2012 under chef Manuel Berganza, it earned one Michelin star in 2014, which it maintained until its reported ...

 

The Music Factory

Pour les articles homonymes, voir TMF. The Music FactoryLogo du réseau The Music FactoryCaractéristiquesCréation 1er mai 1995Disparition 1er novembre 2015Propriétaire Paramount Networks EMEAALangue DiversPays Pays-Bas, BelgiqueSite web www.tmf.beDiffusionAire BelgiqueChronologieMTV Dance (France)Viva (Royaume-Uni et Irlande)Cartoon Network (Italie)modifier - modifier le code - modifier Wikidata The Music Factory, abrégé en TMF, est un réseau international de chaînes de télévision m...

Galibi Order

Turkish Sufi mystic order in Islam This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Galibi Order – news · newspapers · books · scholar · JSTOR (November 2010) (Learn how and when to remove this template message) Part of a series onIslam Beliefs Oneness of God Angels Revealed Books Prophets Day of Resurrection Predestination Pr...

 

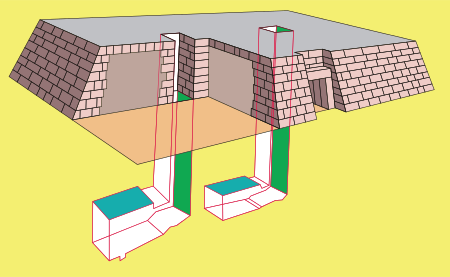
Mastaba

Type of tomb in ancient Egypt Example of a mastaba, the Mastabat al-Fir'aun of Shepseskaf A mastaba (/ˈmæstəbə/ MASS-tə-bə,[1] /ˈmɑːstɑːbɑː/ MAHSS-tah-bah or /mɑːˈstɑːbɑː/ mahss-TAH-bah), also mastabah or mastabat) is a type of ancient Egyptian tomb in the form of a flat-roofed, rectangular structure with inward sloping sides, constructed out of mudbricks or limestone. These edifices marked the burial sites of many eminent Egyptians during Egypt's Early Dynastic Pe...

 

Keponakan Penyihir

Sampul Buku Keponakan Penyihir Keponakan Penyihir (bahasa Inggris: The Magician's Nephew) adalah novel fantasi anak-anak karya C. S. Lewis. Novel ini adalah buku keenam yang dipublikasikan dari ketujuh buku seri The Chronicles of Narnia. Walaupun demikian, bila diurutkan secara kronologi, maka buku ini adalah buku yang pertama. C.S. Lewis mendedikasikan novel ini kepada Keluarga Kilmer. Ringkasan cerita Cerita ini dimulai di London sekitar tahun 1885, ketika dua anak, Digory Kirke dan Polly P...

Новотитаровское сельское поселение

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна  Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...

 

Issey Ogata

Issey Ogata Issey Ogata (イッセー尾形code: ja is deprecated , Issei Ogata, lahir 22 Februari 1952) adalah seorang pemeran dan komedian asal Jepang. Ia meminati drama sejak kecil. Setelah lulus dari SMA Toyotama di Jepang, ia bergabung dengan sebuah perusahaan teatrikal dan tampil di atas panggung. Kemudian ia mengambil kesempatan untuk menjadi seorang entertainer saat ia meraih medali emas di sebuah audisi yang disebut Kelahiran Para Komedian. Kemudian, ia mulai berperan dalam TV Jepang...

 

Equipos participantes en la Copa Mundial de Fútbol de 1938

Equipos participantes de la Copa Mundial Para la III Copa Mundial de Fútbol, que se realizó en Francia entre el 4 de junio y el 19 de junio de 1934, 15 equipos clasificaron a la fase final. Los 15 equipos participantes fueron divididos en una fase final desde los octavos de final, para determinar al campeón del evento. Equipos A la fase final del torneo clasificaron 15 de 34 equipos que participaron en la etapa clasificatoria: uno de Sudamérica, uno de Norteamérica, 12 de Europa (incluye...

العلاقات التشيكية التشيلية

العلاقات التشيكية التشيلية التشيك تشيلي   التشيك   تشيلي تعديل مصدري - تعديل   العلاقات التشيكية التشيلية هي العلاقات الثنائية التي تجمع بين التشيك وتشيلي.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة التشيك ...

 

Kyrgyzstan at the Paralympics

Sporting event delegationKyrgyzstan at theParalympicsIPC codeKGZNPCNational Paralympic Federation of the Kyrgyz RepublicMedals Gold 0 Silver 0 Bronze 0 Total 0 Summer appearances19962000200420082012201620202024Winter appearances201420182022Other related appearances Soviet Union (1988) Unified Team (1992) Kyrgyzstan made its Paralympic Games début at the 1996 Summer Paralympics in Atlanta and has competed in every edition of the Summer Paralympics since then - albeit with delegation...

 

奧林匹克運動會荷屬安地列斯代表團

奥林匹克运动会荷属安的列斯代表團荷屬安的列斯旗幟IOC編碼AHONOC荷属安的列斯奥林匹克委员会網站web.archive.org/web/20101210030408/http://www.naoc.info/（英文）历届奥林匹克运动会参赛记录（总结）夏季奥林匹克运动会195219561960196419681972197619801984198819921996200020042008冬季奥林匹克运动会19881992其他相关赛事参赛记录 独立奥林匹克运动员（2012年） 阿鲁巴（2016年－） 荷兰（20...

Regions of Pennsylvania

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Regions of Pennsylvania – news · newspapers · books · scholar · JSTOR (March 2023) Regions of Pennsylvania in the United States include: Lehigh Valley Main article: Lehigh Valley The Lehigh Valley is named for the Lehigh River, which flows through it...

 

David Payne (artist)

Sweet Summer - 1876 David Payne (1843 – 1894) was a Scottish landscape painter. Biography Payne was born in Annan in the old county of Dumfriesshire,[1] the son of a Mason. He was educated at Annan Academy (along with fellow artist William Ewart Lockhart). He initially made his living as a house painter before becoming an artist. Payne moved to Derby in 1869 and was recorded as living at several places in the county of Derbyshire in the 1880s including Duffield and Barrow upon ...

 

ISDB-T International

Technical standard for digital televisions SBTV redirects here. For the UK youth broadcaster, see SB.TV. List of digital television broadcast standards DVB standards (countries) DVB-T (terrestrial) DVB-T2 DVB-S (satellite) DVB-S2 DVB-S2X DVB-C (cable) DVB-C2 DVB-H (handheld) DVB-NGH DVB-T2-Lite DVB-SH (satellite) DVB-I (service discovery) ATSC standards (countries) ATSC (terrestrial/cable/satellite) ATSC 2.0 ATSC 3.0 ATSC-M/H (mobile/handheld) ISDB standards (countries) ISDB-T (terrestrial) S...

The Gambia (1965–1970)

West African independent sovereign state This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (January 2017) (Learn how and when to remove this message) The Gambia1965–1970 Flag Coat of arms Motto: Progression, Peace, ProgressAnthem: For The Gambia Our HomelandLocation of the Gambia (red) in Western AfricaCapitalBathur...

 

مستشار ألمانيا (منذ 1949)

مستشار جمهورية ألمانيا الاتحادية (بالألمانية: Bundeskanzler)‏  مستشار ألمانيا (منذ 1949) مستشار ألمانيا (منذ 1949) alt شاغل المنصب أولاف شولتس منذ 8 ديسمبر 2021 البلد ألمانيا  اللقب سعادة  عن المنصب مقر الإقامة الرسمي المستشارية الألمانية، برلين، ألمانيا (أساسي)قصر شاومبورغ، بون�...

 

橙汁

此條目没有列出任何参考或来源。 (2009年6月1日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 橙汁 橙汁（英文：Orange juice，在北美洲有時簡稱OJ），是從[橙的果肉]榨出的果汁。其酸酸甜甜的味道，十分可口。有些橙汁含有果肉颗粒，又是另一种风味。 在許多國家，橙汁通常是最常見的飲料之一�...

كأس أيرلندا الشمالية 1993–94

كأس أيرلندا الشمالية 1993–94 تفاصيل الموسم كأس أيرلندا  البلد أيرلندا الشمالية  البطل نادي لينفيلد  عدد المشاركين 32   كأس أيرلندا الشمالية 1992–93  كأس أيرلندا الشمالية 1994–95  تعديل مصدري - تعديل   كأس أيرلندا الشمالية 1993–94 (بالإنجليزية: 1993–94 Irish Cup)‏ هو موسم م�...

 

Moyenne de Lehmer

Construction géométrique des moyennes de Lehmer de deux nombres réels, selon un résultat de Farnsworth et Orr[1]. En mathématiques, la moyenne de Lehmer d'une famille ( x 1 , … , x n ) {\displaystyle (x_{1},\dots ,x_{n})} de nombres réels strictement positifs, portant le nom de Derrick Henry Lehmer, est une moyenne définie par [2]: L p ( x 1 , … , x n ) = ∑ k = 1 n x k p ∑ k = 1 n x k p − 1 , {\displaystyle L_{p}(x_{1},\dots ,x_{n})={\frac {\sum ...