Read other articles:

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2021) دوري نيوزيلندا لكرة القدم 2013–14 تفاصيل الموسم بطولة نيوزيلندا لكرة القدم  النسخة 45  البلد نيوزيلندا  التاريخ بداية:10 نوفمبر 2013  البطل نادي أوكلان�...

18 MusikJenisMusik dan HiburanIndustriMusik dan HiburanDidirikan2011 di JakartaKantorpusatJakarta, IndonesiaProdukMusik dan HiburanSitus webhttp://www.18musik.com 18 Musik adalah perusahaan rekaman asal Indonesia. Perusahaan ini didirikan pada tahun 2000 di Jakarta. Penyanyi terkenal di label rekaman ini seperti Super Girlies, Devi Noviaty, dan masih banyak lagi. Penyanyi/Grup Devi Noviaty Essa Brillian Ever Slkr Super Girlies Dara Fu Gotrie Miss Ronggeng Primadonna Kunci Pop Corn Tiket Manda...

Parliamentary constituency in the United Kingdom, 1868–1918 This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hawick Burghs UK Parliament constituency – news · newspapers · books · scholar · JSTOR (October 2007) (Learn how and when to remove this template message) Hawick BurghsFormer District of burghs ...

Science et Vie Pays France Langue Français Périodicité Mensuelle Genre Vulgarisation scientifique Prix au numéro 4,90 € Diffusion 181 000 ex. (2020) Date de fondation 1913 (il y a 111 ans) Ville d’édition Montrouge Propriétaire Reworld Media Directeur de la rédaction Karine Zagaroli Rédacteur en chef Thomas Cavaillé-Fol ISSN 0036-8369 Site web www.science-et-vie.com modifier  Science et Vie (Science & Vie selon la graphie de la couverture) est un magazine mens...

County in Georgia, United States 31°10′N 83°26′W / 31.167°N 83.433°W / 31.167; -83.433 County in GeorgiaCook CountyCountyCook County Courthouse in AdelLocation within the U.S. state of GeorgiaGeorgia's location within the U.S.Coordinates: 31°10′00″N 83°26′00″W / 31.1667°N 83.4333°W / 31.1667; -83.4333Country United StatesState GeorgiaFounded1918; 106 years ago (1918)Named forPhilip CookSeatAdelLarg...

80th season of top-tier Italian football Football league seasonSerie ASeason1981 (1981)–82Dates13 September 1981 – 16 May 1982ChampionsJuventus (20th title) RelegatedMilanBolognaComoEuropean CupJuventusCup Winners' CupInternazionaleUEFA CupRomaFiorentinaNapoliMatches played240Goals scored474 (1.98 per match)Top goalscorerRoberto Pruzzo(15 goals)← 1980–81 1982–83 → AscoliAvellinoBolognaCagliariCesenaCatanzaroComoFiorentinaGenoaInterMilanJuventusTorinoNapoliRomaUdineseclas...

Huescacomune Huesca – Veduta LocalizzazioneStato Spagna Comunità autonoma Aragona Provincia Huesca AmministrazioneAlcaldeLuis Felipe (PSOE) dal 2015 TerritorioCoordinate42°08′N 0°25′W / 42.133333°N 0.416667°W42.133333; -0.416667 (Huesca)Coordinate: 42°08′N 0°25′W / 42.133333°N 0.416667°W42.133333; -0.416667 (Huesca) Altitudine492 m s.l.m. Superficie161 km² Abitanti52 443 (2011) Densità325,73...

Divorce Attorney ShinPoster promosiHangul신성한, 이혼 Hanja神聖한, 離婚 Arti harfiahSacred DivorceAlih AksaraSinseonghan, ihonMcCune–ReischauerSinsŏnghan, ihon GenreLegalDramaBerdasarkanSacred Divorceoleh Kang Tae-kyungDitulis olehYoo Young-ah[1]SutradaraLee Jae-hoonLim Jun-hyukPemeranCho Seung-wooHan Hye-jinKim Sung-kyunJung Moon-sungMusikHwang Chan-heePark In-youngNegara asalKorea SelatanBahasa asliKoreaJmlh. episode4 (per 12 Maret 2023 (2023-03-12))ProduksiProdus...

  「俄亥俄」重定向至此。关于其他用法，请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號：七葉果之州地图中高亮部分为俄亥俄州坐标：38°27'N－41°58'N, 80°32'W－84°49'W国家 美國加入聯邦1803年3月1日，在1953年8月7日追溯頒定（第17个加入联邦）首府哥倫布（及最大城市）政府 • 州长（英语：List of Governors of {{{Name}}}]]） •&...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна  УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of Everton F.C. international players – news · newspapers · books · scholar · JSTOR (November 2019) (Learn how and when to remove this message) Everton Football Club, an association football club based in Liverpool, Merseyside, was founded in 1878 and com...

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) SMA Yadika Bandar LampungInformasiDidirikan2010JenisSwastaAkreditasiAKepala SekolahDrs . Marulak Hutagalung: tahun 2013 - sekarangJumlah ...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: National Assembly Togo – news · newspapers · books · scholar · JSTOR (May 2024) This article needs to be updated. The reason given is: The 2024 Togolese parliamentary election has been held. Please help update this article to reflect recent event...

Horses running at a ranch in Texas Horses have been an important component of American life and culture since before the founding of the nation. In 2008, there were an estimated 9.2 million horses in the United States,[1] with 4.6 million citizens involved in businesses related to horses.[2][3] There are an estimated 82,000[4] feral horses that roam freely in the wild in certain parts of the country, mostly in the Western United States. While genus E...

Censorship of content in Italy Part of a series onCensorship by country Countries List Albania Algeria Armenia Australia Austria Azerbaijan Bahrain Bangladesh Belarus Bhutan Bolivia Brazil Cambodia Canada Chad China(Hong Kong / overseas) Croatia Cuba Czech Republic Denmark Ecuador Egypt El Salvador Eritrea Finland France(Ancien Régime) Germany(Nazi / Democratic Republic / Federal Republic) Greece Guatemala Honduras India Indonesia(Dutch East Indies) Iran(Islamic) Iraq Ireland Israel Italy(Wo...

1957 film by Josef von Sternberg Jet PilotTheatrical release posterDirected byJosef von SternbergWritten byJules FurthmanProduced byJules FurthmanHoward Hughes (presenter)StarringJohn WayneJanet LeighCinematographyWinton C. HochEdited byJim Wilkinson (Ed supv)Michael R. McAdamHarry MarkerWilliam M. MooreMusic byBronislau KaperProductioncompanyRKO Radio PicturesDistributed byUniversal-InternationalRelease dates September 25, 1957 (1957-09-25) (Premiere-Los Angeles) October&#...

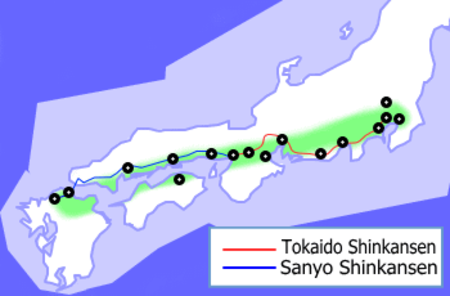
География Японии Часть света Азия Регион Восточная Азия Координаты 36° с. ш., 138° в. д. Площадь 62-я в мире 377 976,41 км² вода: 12,06901% % суша: 87,93099% % Береговая линия 29 751 км Границы 0 Высшая точка 3776 м (гора Фудзи) Низшая точка −4 м (Хатирогата) Крупнейшая река Синано (река) (367 км) Кру...

André Warnod, Les Berceaux de la jeune peinture, Paris, 1925.Illustration d'Amedeo Modigliani. L'École de Paris[note 1] désigne l'ensemble des artistes, dont un grand nombre d'étrangers, qui ont travaillé à Paris de 1900 à 1960, faisant de cette ville un centre d'art de premier plan dans le monde. Signification de l'expression « École de Paris » Cette expression pose un problème lorsqu’on l'utilise pour désigner un groupe d’artistes en particulier. En réalité, elle...

Set of elements in any of some sets Union of two sets:   A ∪ B {\displaystyle ~A\cup B} Union of three sets:   A ∪ B ∪ C {\displaystyle ~A\cup B\cup C} The union of A, B, C, D, and E is everything except the white area. In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection.[1] It is one of the fundamental operations through which sets can be combined and related to each other. A nullary union refer...

Geometric arrangements of points, foundational to Lie theory This article is about root systems in mathematics. For plant root systems, see Root. Lie groups and Lie algebras Classical groups General linear GL(n) Special linear SL(n) Orthogonal O(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n) Simple Lie groups Classical An Bn Cn Dn Exceptional G2 F4 E6 E7 E8 Other Lie groups Circle Lorentz Poincaré Conformal group Diffeomorphism Loop Euclidean Lie algebras Lie...