円周率が22/7より小さいことの証明
|
Read other articles:

جزء من سلسلة مقالات حولالإسلام حسب البلد الإسلام في إفريقيا أنغولا بنين بوتسوانا بوركينا فاسو بوروندي الكاميرون الرأس الأخضر أفريقيا الوسطى نشاد الجزائر جزر القمر الكونغو الديمقراطية الكونغو ساحل العاج جيبوتي مصر غينيا الاستوائية إريتريا إثيوبيا الغابون غامبيا غانا غي...

Rencontre entre le Premier vice-président Mehriban Aliyeva et le ministre d'État français auprès du ministre de l'Europe et des Affaires étrangères. Ministre d'État est un titre gouvernemental utilisé dans divers pays. Dans certains cas, il indique une prééminence protocolaire de son titulaire au sein d'un gouvernement (France, Portugal, Côte d'Ivoire, Mali, Niger, République démocratique du Congo, Tunisie). En Belgique, il s'agit d'un titre accordé par le roi à des personnalit...

American politician and businessman (1898–1976) Bill BlakleyBlakley in 1961United States Senatorfrom TexasIn officeJanuary 3, 1961 – June 14, 1961Appointed byPrice DanielPreceded byLyndon B. JohnsonSucceeded byJohn TowerIn officeJanuary 15, 1957 – April 28, 1957Appointed byAllan ShiversPreceded byPrice DanielSucceeded byRalph Yarborough Personal detailsBornWilliam Arvis BlakleyNovember 17, 1898Miami Station, Missouri, U.S.DiedJanuary 5, 1976(1976-01-05) (aged 77)D...

1644 battle of the Thirty Years' War Not to be confused with Battle of Freiberg. Battle of FreiburgPart of Thirty Years' WarCondé at FreiburgDate3 August, 5 August, 9 August 1644LocationFreiburg, Baden-WürttembergResult Disputed [1][2][3][4]Belligerents France Holy Roman Empire Electorate of BavariaCommanders and leaders Condé Turenne Franz von Mercy Johann von WerthStrength c. 16,000 [5][6] c. 13,000 [a]Casualties a...

GulliDiluncurkan18 November 2005PemilikM6 GroupPangsa pemirsa3.3% (TNT) (Juni 2007, [1])Negara PrancisSitus webwww.gulli.frwww.6play.fr/gulli Gulli merupakan sebuah jaringan televisi Prancis baru yang ditujukan pada program anak-anak. Tersedia melalui televisi terrestrial digital TNT dengan kerjasama dengan Lagardère Active dan Canal J, dan France Télévisions dengan program anak-anak dari France 3. Saluran ini mmengudara dari 6:30 hingga 23:00 setiap hari. Gulli juga dikenal sebagai C...

Renato Ghezzi Nazionalità Italia Calcio Ruolo Attaccante Termine carriera 1948 Carriera Squadre di club1 1932-1934 Rhodense? (?)1937-1938 Casale29 (13)1939-1941 Alessandria57 (23)1941-1942 Brescia7 (0)1945-1946 Gladiator? (?)1946-1948 Torrese57 (16) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Modifica dati su Wikidata · Manuale Renato Ghezzi (Rho,...

Ancient Greek city, forerunner of Constantinople This article is about the ancient city. For the city in the late Roman period (330–1453), see Constantinople. For the Ottoman and modern city (after 1453), see Istanbul. For the empire, see Byzantine Empire. For other uses, see Byzantium (disambiguation). ByzantiumByzantionLocation of Byzantion, corresponding to the modern-day Fatih district of IstanbulAlternative nameByzantion (earlier Greek name), Nova Roma (New Rome)LocationFatih, Ist...

Integrated circuit technology that integrates radio-frequency, analog and digital electronics This article may misquote or misrepresent many of its sources. Please see the cleanup page for more information. Editors: please remove this warning only after the diffs listed [[Wikipedia talk:Requests for comment/Jagged 85/{{{subpage}}}|here]] have been checked for accuracy. (July 2022) RF CMOS is a metal–oxide–semiconductor (MOS) integrated circuit (IC) technology that integrates radio-frequen...

Hanover Square from Stow's London Squares (1750), looking north across Marylebone, which was then not built up on the horizon. Hanover Square is a green square in Mayfair, Westminster, south west of Oxford Circus where Oxford Street meets Regent Street. Six streets converge on the square which include Harewood Place with links to Oxford Street, Princes Street, Hanover Street, Saint George Street, Brook Street and Tenderden Street, linking to Bond Street and Oxford Street.[1] History ...

2015 studio album by Marcus MillerAfrodeeziaStudio album by Marcus MillerReleasedMarch 16, 2015 (2015-03-16)Studio 1172 Bounce (North Brunswick, New Jersey) Jankland Recording Studios (New Jersey) Audible Images (Pittsburgh, Pennsylvania) GBP Studios (East Landing, Missouri) Grand Street Recording (Brooklyn, New York) Queens Studios (Queens, New York) Jack Of All Studios (Quincy, Massachusetts) Rustic Space (Portland, Maine) La Louisianne Recording Studios (Layfaette, L...

Area of tissue in the eye This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Trabecular meshwork – news · newspapers · books · scholar · JSTOR (December 2008) (Learn how and when to remove this message) Trabecular meshworkEnlarged general view of the iridial angle. (When enlarged, visible with older label of 't...

Office skyscraper in Montreal, Quebec, Canada and tallest building in Quebec. 1250, boulevard René-LévesqueGeneral informationTypeOfficeArchitectural stylePostmodernLocation1250 René-Lévesque Boulevard, Montreal, Quebec, CanadaCoordinates45°29′50″N 73°34′13″W / 45.497323°N 73.570381°W / 45.497323; -73.570381Completed1992OwnerBentallGreenOak (Sunlife)ManagementBentallGreenOakHeightArchitectural226.5 metres (743 ft)Roof199 metres (653 ft)Technic...

Ad problema geometricum responsum, 1613 Giovanni Camillo Glorioso, o Gloriosi (Giffoni Valle Piana, 1572 – Napoli, 8 gennaio 1643), è stato un matematico e astronomo italiano.[1] Fu amico di Marino Ghetaldi e successore di Galileo Galilei all'Università di Padova. Indice 1 Biografia 2 Opere 3 Note 4 Bibliografia 5 Altri progetti 6 Collegamenti esterni Biografia La firma di Glorioso nell'estratto di una procura Giovanni Camillo Glorioso nacque a forse a Gauro, allora territorio di ...

Fictional character Patron-MinetteThe Patron-Minette gang in their hide-out in the Paris sewer system. Illustration by Pierre-Georges JeanniotCreated byVictor HugoIn-universe informationNationalityFrench Patron-Minette was the name given to a street gang in Victor Hugo's 1862 novel Les Misérables and the musical of the same name. The gang consisted of five criminals: Montparnasse, Claquesous, Babet, and Gueulemer, Brujon. They were well acquainted with the Thénardiers, who recruited them to...
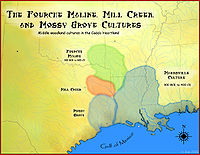
History of Louisiana By year Pre-statehood U.S. Civil War Post-Civil War Topics: African-Americans - Cities - Politics United States portalvte The history of the area that is now the U.S. state of Louisiana, can be traced back thousands of years to when it was occupied by indigenous peoples. The first indications of permanent settlement, ushering in the Archaic period, appear about 5,500 years ago. The area that is now Louisiana formed part of the Eastern Agricultural Complex. The Marksv...

埼玉県の行政機関埼玉県教育委員会役職教育長 高田直芳概要所在地 埼玉県さいたま市浦和区高砂3-15-1定員 教育長及び5人の委員ウェブサイト 埼玉県教育委員会テンプレートを表示 埼玉県教育委員会(さいたまけんきょういくいいんかい)は、埼玉県の教育委員会である。さいたま市浦和区に本部を置く。 概要 埼玉県内の教育に関する事務を所掌する行政委員会であ�...

Animated fantasy sitcom created by Matt Groening DisenchantmentGenre Adult animation Animated sitcom Fantasy Adventure Satire Created byMatt GroeningDeveloped by Matt Groening Josh Weinstein Voices of Abbi Jacobson Eric André Nat Faxon John DiMaggio Tress MacNeille Matt Berry David Herman Maurice LaMarche Lucy Montgomery Billy West ComposerMark MothersbaughCountry of originUnited StatesOriginal languageEnglishNo. of seasons3 (5 parts)No. of episodes50 (list of episodes)ProductionExecutive pr...

Swiss watchmaker This article is about the watch company. For other uses of the term swatch, see Swatch (disambiguation). For the parent group, see The Swatch Group. Swatch Ltd.Swatch store in Namba, Osaka, JapanCompany typeSubsidiaryIndustryWatchmakingFounded1983; 41 years ago (1983)HeadquartersBiel, SwitzerlandKey peopleNick Hayek Jr. (chairman, president)ProductsWristwatchesParentThe Swatch GroupSubsidiariesFlik FlakWebsiteswatch.com Swatch is a Swiss watchmaker founded i...

Para el conjunto de territorios gobernados por las dinastías hispánicas entre los siglos xvi y xx, véase Imperio español. Monarquía HispánicaMonarquía Católica Monarquía compuesta 1479-1716 Enseña naval y militar Mapa de los territorios regidos por Felipe II en 1598 Territorios adscritos al Consejo de Castilla Territorios adscritos al Consejo de Aragón Territorios adscritos al Consejo de Portug...

Canadian mathematician Kenneth Davidson Kenneth Ralph Davidson (born 1951 in Edmonton, Alberta)[1] is Professor of Pure Mathematics at the University of Waterloo. He did his undergraduate work at Waterloo and received his Ph.D. under the supervision of William Arveson at the University of California, Berkeley in 1976. Davidson was Director of the Fields Institute from 2001 to 2004. His areas of research include operator theory and C*-algebras. Since 2007 he has been appointed Universi...


![{\displaystyle {\begin{aligned}0&<\int _{0}^{1}\!{\frac {x^{4}(1-x)^{4}}{1+x^{2}}}\,{\rm {d}}x\\&{\phantom {<}}=\int _{0}^{1}\!{\frac {x^{4}-4x^{5}+6x^{6}-4x^{7}+x^{8}}{1+x^{2}}}\,{\rm {d}}x\\&{\phantom {<}}=\int _{0}^{1}\!{\biggl (}x^{6}-4x^{5}+5x^{4}-4x^{2}+4-{\frac {4}{1+x^{2}}}{\biggr )}\,{\rm {d}}x\\&{\phantom {<}}={\biggl [}{\frac {x^{7}}{7}}-{\frac {2x^{6}}{3}}+x^{5}-{\frac {4x^{3}}{3}}+4x-4\arctan {x}\,{\biggr ]}_{0}^{1}\\&{\phantom {<}}={\frac {1}{7}}-{\frac {2}{3}}+1-{\frac {4}{3}}+4-\pi \\&{\phantom {<}}={\frac {22}{7}}-\pi \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5c1409a41d329b5cc8220d4e26b9181f7282c38)























