Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Laku lajak, peran berlebihan, atau akting berlebihan (Inggris: overactingcode: en is deprecated ) mengacu kepada tingkah laku atau perbuatan yang berlebihan. Dalam seni peran, laku lajak berarti tindakan yang dilakukan oleh pemeran secara berlebihan da...

Artikel ini bukan mengenai Bailee Madison. Madison BaileyBailey di The Jennifer Hudson Show pada tahun 2023LahirKernersville, Carolina Utara, Amerika SerikatPekerjaanPemeranmodelTahun aktif2015–sekarang Madison Bailey adalah pemeran dan model asal Amerika Serikat. Ia berperan sebagai Kiara Kie Carrera dalam seri drama remaja Netflix Outer Banks (2020–sekarang).[1] Filmografi Film Tahun Judul Peran Catatan 2018 Bottle Girl Jackie 2020 Discarded Things Daniella Impractical Joke...

Kris Kobach Sekretaris Negara Bagian Kansas ke-31Masa jabatan10 Januari 2011 – 14 Januari 2019GubernurSam BrownbackJeff Colyer PendahuluChris BiggsPenggantiScott SchwabKetua Partai Republik KansasMasa jabatan28 Januari 2007 – 31 Januari 2009 PendahuluTim ShallenburgerPenggantiAmanda Adkins Informasi pribadiLahirKris William Kobach26 Maret 1966 (umur 58)Madison, Wisconsin, Amerika SerikatPartai politikRepublikSuami/istriHeather Mannschreck ​(m. 202...

العلاقات البحرينية الجنوب أفريقية البحرين جنوب أفريقيا   البحرين   جنوب أفريقيا تعديل مصدري - تعديل   العلاقات البحرينية الجنوب أفريقية هي العلاقات الثنائية التي تجمع بين البحرين وجنوب أفريقيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة...

Political program launched by Lyndon B. Johnson in 1964–65 For the 1960s band featuring Grace Slick, see The Great Society (band). The pens used by President Lyndon B. Johnson to sign Great Society legislation The Great Society was a set of domestic programs in the United States launched by President Lyndon B. Johnson in 1964 and 1965. The term was first referenced during a 1964 speech by Johnson at Ohio University,[1] then later formally presented at the University of Michigan, and...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أغسطس 2018) بيرند ديرهر (بالألمانية: Bernd Dreher)‏    معلومات شخصية الميلاد 2 نوفمبر 1966 (العمر 57 سنة)ليفركوزن  الطول 1.87 م (6 قدم 1 1⁄2 بوصة) مركز اللعب حارس مر�...

Per Olov Enquist Per Olov Enquist (Skellefteå, 23 settembre 1934 – Vaxholm, 25 aprile 2020) è stato uno scrittore, sceneggiatore, giornalista e cronista sportivo svedese. Per Olov Enquist nel 2012 Le sue opere sono tradotte all'estero in oltre 23 lingue. Indice 1 Biografia 2 Riconoscimenti 3 Filmografia 3.1 Sceneggiatore 4 Opere 5 Altri progetti 6 Collegamenti esterni Biografia Dopo essersi laureato in letteratura svedese all'Università di Uppsala, fra il 1965 e il 1976 lavorò come gior...

Pour les autres membres de la famille, voir Famille d'Irumberry de Salaberry. Charles-Marie d'Irumberry de SalaberryFonctionsMembre de la Chambre des députés des départementsQuatrième législature de la Seconde Restauration (d)Loir-et-Cher24 novembre 1827 - 16 mai 1830Conseiller général de Loir-et-Cherà partir de 1825Membre de la Chambre des députés des départementsTroisième législature de la Seconde Restauration (d)Loir-et-Cher25 février 1824 - 5 novembre 1827Membre de la Chamb...

Coat of arms of Count Colonna-Walewski Aleksander Colonna-Walewski Maria Walewska; portrait by François Gérard Michał Walewski; portrait byJózef Pitschmann (1788) The Walewski family (plural: Walewscy, feminine form: Walewska) was an influential Polish noble family which originated from Walewice in Łęczyca Land, firstly mentioned in 1382. History The family issued 15 senators in the First Polish Republic (1574-1795), one senator of the Polish Kingdom (1819-1831), 4 Knights of the Order ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2020. The Warrior Queen of JhansiSutradaraSwati BhiseProduserSwati BhiseCharles SalmonDitulis olehSwati BhiseDevika BhisePemeranDevika BhiseRupert EverettDerek JacobiPenata musikTuomas KantelinenSinematograferSeamus DeasyPenyuntingOral Norrie OttayDist...

This is a list of bacon substitutes. A number of substitutes exist for people who, for ethical, environmental, health, religious, or other reasons, prefer not to eat bacon. The flavor of smoked paprika resembles cooked bacon to some people. Bacon substitutes Name Image Origin Description Baconnaise United States A kosher mayonnaise-based product developed by J&D's Foods that is prepared to taste like bacon, Baconnaise is vegetarian and contains no bacon.[1] Its creators have also...

МифологияРитуально-мифологическийкомплекс Система ценностей Сакральное Миф Мономиф Теория основного мифа Ритуал Обряд Праздник Жречество Мифологическое сознание Магическое мышление Низшая мифология Модель мира Цикличность Сотворение мира Мировое яйцо Мифическое �...

† Стеллерова корова Муляж стеллеровой коровы в Лондонском музее естествознания Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстно�...

斯洛博丹·米洛舍维奇Слободан МилошевићSlobodan Milošević 南斯拉夫联盟共和国第3任总统任期1997年7月23日—2000年10月7日总理拉多耶·孔蒂奇莫米尔·布拉托维奇前任佐兰·利利奇（英语：Zoran Lilić）继任沃伊斯拉夫·科什图尼察第1任塞尔维亚总统任期1991年1月11日[注]—1997年7月23日总理德拉古京·泽莱诺维奇（英语：Dragutin Zelenović）拉多曼·博若维奇（英语：Radoman Bo...

Finite volume method in partial differential equations In the study of partial differential equations, the MUSCL scheme is a finite volume method that can provide highly accurate numerical solutions for a given system, even in cases where the solutions exhibit shocks, discontinuities, or large gradients. MUSCL stands for Monotonic Upstream-centered Scheme for Conservation Laws (van Leer, 1979), and the term was introduced in a seminal paper by Bram van Leer (van Leer, 1979). In this paper he ...

A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (February 2020) (Learn how and when to remove this message) Georgetown University School of Continuing StudiesSeal of Georgetown UniversityFormer namesSummer School (1953–1970)School for Summer and Continuing Education (1970–2004)TypePrivateEstablished1970Pa...

Train station in Wisconsin La Crosse, WIThe westbound Empire Builder at La Crosse station in 2023General informationLocation601 Saint Andrew StreetLa Crosse, WisconsinUnited StatesCoordinates43°50′00″N 91°14′50″W / 43.8334°N 91.2472°W / 43.8334; -91.2472Owned byCity of La CrosseLine(s)CPKC Tomah SubdivisionPlatforms1 side platformTracks2Connections MTU:  6  SMRT:  Yellow ConstructionParkingYesBicycle facilitiesYesAccessibleYesOther infor...

Queen consort of Poland Catherine OpalińskaPortrait by Jean-Baptiste van Loo, 1725Queen consort of PolandGrand Duchess consort of LithuaniaTenure4 October 1704 – 8 August 1709Coronation4 October 1705Tenure12 September 1733 – 27 January 1736Duchess consort of LorraineTenure9 July 1737 – 19 March 1747Born(1680-10-13)13 October 1680Poznań, Poland, Polish–Lithuanian CommonwealthDied19 March 1747(1747-03-19) (aged 66)Lunéville, Duchy of Lorraine, Holy Roman EmpireBurialNotre-Dame-d...

British-built railroad steam locomotive John BullJohn Bull, c. 1895Type and originPower typeSteamBuilderRobert Stephenson and CompanyBuild date1831; 193 years ago (1831)SpecificationsConfiguration:​ • Whyte2-4-0 (built by Stephenson as an 0-4-0) • UIC1′1A (built as B)Gauge4 ft 8+1⁄2 in (1,435 mm) standard gaugeDriver dia.4 ft 6 in (1,372 mm)[1]Wheelbase4 ft 11 in (1,499 mm)...

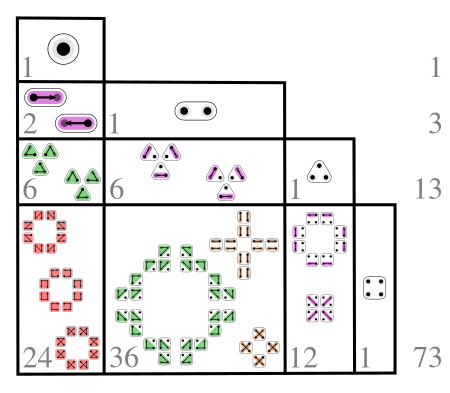
Mathematical sequence Illustration of the unsigned Lah numbers for n and k between 1 and 4 In mathematics, the (signed and unsigned) Lah numbers are coefficients expressing rising factorials in terms of falling factorials and vice versa. They were discovered by Ivo Lah in 1954.[1][2] Explicitly, the unsigned Lah numbers L ( n , k ) {\displaystyle L(n,k)} are given by the formula involving the binomial coefficient L ( n , k ) = ( n − 1 k − 1 ) n ! k ! {\displaysty...