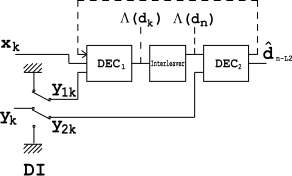
Turbo codiciI turbo codici sono una classe di codici di correzione degli errori ad alte prestazioni, che trovano impiego nelle comunicazioni satellitari nello spazio profondo ed in altre applicazioni in cui i progettisti puntano ad avere il massimo trasferimento di informazione su una banda limitata in presenza di un segnale ricevuto affetto da rumore. I codici turbo sono stati teorizzati da Claude Berrou, Alain Glavieux e Punya Thitimajshima presentati nel 1993 ad una conferenza dell'IEEE[1]. I ricercatori di più atenei verificarono i risultati di Berrou, accorgendosi solo in un secondo momento che i risultati mostrati dal francese non andavano al di sotto di probabilità di errore di 10^-5, scoprendo poi che le curve di errore non decrescevano rapidamente dopo questo valore[senza fonte]. Bisogna ricordare che l'algoritmo di Berrou non è completamente originale. Infatti Robert Gallager, geniale studente e ora insegnante del Massachusetts Institute of Technology, propose già con la sua tesi di dottorato un algoritmo di decodifica, chiamato belief propagation, per lungo tempo passato inosservato e successivamente ripreso da Berrou. Inoltre la stessa idea dei codici turbo è riconducibile ad alcuni lavori di Robert Gallager, sebbene Berrou abbia il merito di avere scelto la soluzione parallela anziché quella seriale, poiché per sua stessa ammissione la prima forma risultava di più semplice implementazione[senza fonte]. I codici turbo sono ancora ad oggi oggetto di ricerche in numerose università del mondo, allo scopo di raffinarli e di ottenere implementazioni più efficienti. Nella teoria dell'informazione, i turbo codici (originariamente Turbocodes, in francese) sono una classe di codici Forward Error Correction (FEC) ad alte prestazioni sviluppati intorno al 1990-91 (ma pubblicati per la prima volta nel 1993), le prime codifiche capaci di avvicinarsi al massimo teorico della capacità del canale teorema di Shannon–Hartley, il massimo teorico per la velocità alla quale è ancora possibile una comunicazione affidabile dato un livello di rumore specifico. I turbo codici sono utilizzati nelle comunicazioni mobili 3G/4G (ad es. In UMTS e LTE) e nelle comunicazioni satellitari (nello spazio profondo) così come altre applicazioni dove i progettisti cercano di ottenere un trasferimento affidabile delle informazioni tramite collegamenti di comunicazione, dati i limiti di larghezza di banda o di latenza e la presenza di rumore dannoso per i dati. I turbo codici sono attualmente in competizione con i codici LDPC (Low-Density-Parity-Check-Code) che offrono prestazioni comparabili. Il nome "turbo code" deriva dal ciclo di feedback in decodifica, perciò è stato associato alla retro-alimentazione dai gas di scarico utilizzata per la sovralimentazione dei motori turbo, Hagenauer ha sostenuto che il termine turbo in tal senso è improprio poiché non vi è alcun feedback verso il processo di codifica nell'encoder,[2]. In ogni caso, il termine turbo, nell'uso popolare, rende bene l'idea di un sistema ingegnoso, veloce e potente. StoriaLa prima domanda di brevetto per i turbo codici è stata depositata il 23 aprile 1991. La domanda di brevetto indica Claude Berrou come l'unico inventore dei codici turbo. La registrazione del brevetto ha portato a numerosi brevetti tra cui il brevetto US 5.446.747 US Patent 5,446,747, che è scaduto il 29 agosto 2013. Il primo documento pubblico sui turbo codici fu "Near Shannon Limit Error-correcting Coding and Decoding: Turbo-codes".[3] Questo documento è stato pubblicato nel 1993 negli Atti della Conferenza Internazionale delle Comunicazioni IEEE. Il documento del 1993 era composto da tre distinti contributi messi insieme per vincoli di spazio. La fusione ha fatto sì che il documento elencasse tre autori: Berrou, Glavieux, e Thitimajshima (da Télécom Bretagne, ENST Bretagne, Francia). Tuttavia dalla domanda di brevetto originale è chiaro che Claude Berrou è l'unico inventore dei turbo codici e che gli altri autori del lavoro hanno fornito del materiale diverso rispetto ai concetti chiave dei turbo codici. I turbo codici furono così rivoluzionari al momento della loro introduzione che molti esperti nel campo della codifica non credettero ai risultati riportati. Quando la performance fu confermata, ebbe luogo una piccola rivoluzione nel mondo della codifica che ha portato allo studio di molti altri tipi di elaborazione di segnale iterativa. La prima classe di codice turbo era il codice convoluzionale concatenato parallelo (PCCC). Dopo l'introduzione del primo turbo codice parallelo nel 1993, sono state realizzate molte altre classi di turbo codici, incluse le versioni seriali dei codici convoluzionali seriali concatenati e dei codici ripetuti-accumulati. Metodi di decodifica turbo iterativi sono stati applicati anche ai più convenzionali sistemi FEC, compresi i codici convoluzionali corretti Reed-Solomon, sebbene questi sistemi di decoder iterativi siano troppo complessi per implementazioni pratiche. La turbo equalizzazione a sua volta è stata derivata dai concetti di turbo codifica. Oltre all'invenzione dei turbo codici, Claude Berrou ha anche sviluppato i codici ricorsivi sistematici convoluzionali (RSC), utilizzati nell'esempio di implementazione dei turbo codici descritti nel brevetto (i turbo codici che usano i codici RSC sembrano funzionare meglio di quelli che non li usano). Prima dei codici turbo, le migliori implementazioni FEC erano costituite da codifiche seriali concatenate basate su un codice di correzione degli errori esterno Reed-Solomon combinato con un codice interno convoluzionale a lunghezza corta algoritmo di Viterbi, noto anche come codice RSV. In un saggio successivo, Berrou ha generosamente riconosciuto l'intuizione di "G. Battail, J. Hagenauer e P. Hoeher, che, alla fine degli anni '80, hanno acceso l'interesse per l'elaborazione probabilistica". Aggiungendo che " R. Gallager e M. Tanner avevano già immaginato tecniche di codifica e decodifica i cui principi generali erano strettamente correlati," anche se i calcoli necessari erano impraticabili a quel tempo.[4] Un esempio di encoderEsistono molti casi diversi di turbo codici, che utilizzano diversi componenti di codificatori, rapporti di input/output, interleaver e pattern di foratura. Questo esempio di implementazione dell'encoder descrive un classico codificatore turbo e mostra la progettazione generale dei turbo codici paralleli. Questa implementazione dell'encoder invia tre sotto-blocchi di bit. Il primo sottoblocco è il blocco m-bit dei dati del payload o carico utile che è spedito senza modifiche (codifica sistematica). Il secondo sottoblocco è costituito da n/2 bit di parità calcolati dai dati del payload utilizzando un codice convoluzionale sistematico ricorsivo (codice RSC). Il terzo sottoblocco è costituito da n/2 bit di parità calcolati su una permutazione nota dei bit del payload, ancora utilizzando un codice RSC. Pertanto due sottogruppi ridondanti ma diversi di bit di controllo di parità sono inviati insieme al carico utile. Il blocco completo è composto da m + n bit di dati, con rapporto D/C (Dati/Controllo) m / ( m + n ). La permutazione dei bit del payload tra le i due RSC in parallelo viene eseguito da un dispositivo chiamato interleaver. L'interleaver installato tra i due codificatori (e i decodificatori) è utilizzato per diffondere e sfumare i picchi di errore prodotti sull'output dal rumore che affligge il mezzo trasmissivo. Dal punto di vista dell'hardware, il codificatore complessivo consiste di due codificatori RSC in parallelo, C1 e C2, come illustrato in figura, che sono collegati tra loro usando uno schema di concatenazione parallela: Nella figura, M è un registro di memoria. La linea di ritardo e l'interleaver portano i bit di input dk al secondo encoder ad apparire in sequenze diverse rispetto al primo encoder. A ogni iterazione la sequenza di ingresso dk appare in uscita xk (codifica sistematica) con l'aggiunta dei bit di parità y1k o y2k. Se i due encoder C1 eC2 sono utilizzati rispettivamente in un numero di iterazioni n1 e n2, le loro velocità sono rispettivamente uguali a Il decoderIl decodificatore è costruito in modo simile all'encoder. Due decodificatori elementari sono interconnessi tra loro ma in modo seriale non in parallelo. Il decodificatore funziona a bassa velocità (es. ) quindi è riferito al codificatore e corrispondentemente sta per il . produce una decisione di tipo soft decision che causa un ritardo . Lo stesso ritardo prodotto dalla linea di ritardo nell'encoder. L'operazione causa un ritardo . Il blocco DI è un modulo di demultiplexing e inserimento di zeri che funziona come un doppio interruttore, reindirizzando alternativamente i bit di input a e a , e nello stato OFF alimenta entrambi gli ingressi and con dei bit di riempimento (zeri). Consideriamo un canale AWGN senza memoria AWGN e assumiamo che alla k-esima iterazione il decodificatore riceva una coppia di variabili casuali: dove e sono componenti di rumore indipendenti con la stessa varianza . è il bit k-mo proveniente dall'encoder . Le informazioni ridondanti sono demultiplexate e inviate attraverso DI a (dove ) e a (dove ). prende una decisione soft; i.e.: e la consegna a . è il cosiddetto logaritmo del rapporto di verosimiglianza (LLR). è la è la probabilità a posteriori (APP) del bit di dati, cioè la probabilità nell'interpretare un bit ricevuto come . Prendendo in considerazione l'LLR, produce una decisione hard; cioè un bit decodificato. L'Algoritmo di Viterbi non è in grado di calcolare l'APP, quindi non può essere utilizzato in . Qui può essere usato utilizzato un algoritmo BCJR modificato BCJR algorithm. Per invece l'algoritmo di Viterbi è appropriato. Tuttavia, la struttura rappresentata non è ottimale, perché utilizza solo una parte delle informazioni ridondanti disponibili. Per migliorare la struttura, viene utilizzato un ciclo di feedback (linea tratteggiata in figura). Approccio alla decisione SoftIl front-end del decoder produce un numero intero per ogni bit nel flusso di dati. Questo numero intero è una misura di quanto è probabile che il bit sia uno 0 o 1 ed è anche chiamato soft bit. Il numero intero può spaziare nell'intervallo [-127, 127], dove:
Questo introduce un aspetto probabilistico al flusso di dati dal front-end ma trasmette più informazioni su ogni bit rispetto a un semplice 0 o 1. Ad esempio, per ciascun bit, il front end di un ricevitore tradizionale deve decidere se una tensione analogica interna è al di sopra o al di sotto di un determinato livello di tensione di soglia. Per un decodificatore di turbo-codice, il front-end fornirebbe una misura di quanto è distante la tensione interna dalla soglia data. Per decodificare il blocco di dati m + n, il front-end del decoder crea un blocco di probabilità, con una misura di verosimiglianza per ogni bit nel flusso di dati. Ci sono due decodificatori paralleli, uno per ciascuno dei n⁄2 sottoblocchi di bit di parità. Ciascun decodificatore usa un sottoblocco di probabilità per i dati del payload m (il decodificatore che lavora sul secondo sotto-blocco di parità conosce la permutazione di bit che ha usato il secondo codificatore). Risoluzione delle ipotesi per trovare i bitL'innovazione chiave dei turbo codici è il modo in cui utilizzano i dati di probabilità per riconciliare le differenze tra i due decodificatori. Ciascuno dei due decodificatori convoluzionali genera un'ipotesi di fiducia (con relativa probabilità) per la sequenza ricevuto degli m bit relativi al carico utile. Le due sequenze d'ipotesi sui bit vengono confrontate e se concordano il lavoro è finito, mentre se differiscono, i decodificatori si scambiano le probabilità che hanno per ciascun bit nell'ipotesi. Ciascun decodificatore incorpora le stime di probabilità derivate dall'altro decodificatore per generare una nuova ipotesi per i bit m del carico utile. Quindi confrontano queste nuove ipotesi. Questo processo iterativo continua fino a quando i due decodificatori giungono alla stessa ipotesi sulla sequenza 'm' di bit del payload, tipicamente i risultati convergono (o divergono) in 4 o 10 cicli. Si può tracciare un'analogia tra questo processo e quello di risolvere enigmi a riferimenti incrociati come i cruciverba o i sudoku. Consideriamo un cruciverba parzialmente completato e probabilmente sbagliato. Due risolutori di rompicapo (decodificatori) cercano di risolverlo: uno possiede gli indizi (bit di parità) "verticali" e l'altro possiede gli indizi "orizzontali". Per iniziare, entrambi i solutori ipotizzano delle risposte alle domande, annotando quanto sono sicuri di ciascuna lettera (bit del payload). Quindi confrontano le ipotesi scambiandosi reciprocamente risposte e valutazioni di quando sono fiduciosi delle risposte, notando dove e come si differenziano. Sulla base di queste nuove conoscenze, entrambi forniscono risposte aggiornate e nuove valutazioni di fiducia, ripetendo l'intero processo fino a quando non convergono sulla stessa soluzione. PrestazioniI codici Turbo funzionano bene grazie alla combinazione dell'aspetto casuale del codice con la struttura di decodifica fisicamente realizzabile. I codici Turbo sono affetti da un calo improvviso di prestazioni al peggiorare del rapporto segnale rumore, detto error floor, in altre parole o correggono tutto bene oppure, oltre una certa soglia di rumore, non correggono più affatto. Applicazioni pratiche dei turbo codiciTelecomunicazioni:
Formulazione bayesianaDal punto di vista dell'intelligenza artificiale, i turbo codici possono essere considerati come un'istanza di propagazione delle credenze fiduciarie ad anello nelle reti bayesiane Rete bayesiana.[6] Note
Voci correlateCollegamenti esterni
|