|
Terzo suono di Tartini
Con terzo suono di Tartini, detto anche suono risultante o suono di combinazione, ci si riferisce a un particolare fenomeno acustico evidenziato da Giuseppe Tartini all'inizio del XVIII secolo, ma con ogni probabilità conosciuto già prima.
Storia
Durante il periodo in cui insegnava violino al Teatro della Fenice di Senigallia, nel 1714, il violinista Giuseppe Tartini intuì che suonando un bicordo al violino si può percepire contemporaneamente un terzo suono, più grave, detto appunto "terzo suono". In sostanza si "materializza" una nota inattesa la cui frequenza corrisponde alla differenza delle frequenze dei due suoni fondamentali originari. La scoperta fu merito dell'eccezionale orecchio musicale di Tartini, in quanto è spesso non facile percepire il terzo suono.
Ad esempio, eseguendo un suono da 512 Hz e contemporaneamente uno da 640 Hz, si sentirà anche un suono, più grave, di 128 Hz (due ottave sotto la fondamentale di 512 Hz). Il fenomeno avviene con bicordi relativi a svariati intervalli musicali "semplici", compresi micro-intervalli di tono maggiore (9/8) e minore (10/9). Gli intervalli che Tartini definisce "semplici" sono correntemente chiamati puri o naturali, nel senso che corrispondono a rapporti fra frequenze date da numeri razionali. E poiché lo spettro armonico dei suoni complessi, quali quelli di un violino, segue una rigorosa legge di progressione aritmetica delle frequenze dei suoni che lo costituiscono, la naturalità "fisica" di un intervallo si ottiene quando i primi suoni armonici prodotti dai due fondamentali costituenti l'intervallo coincidono e non producono effetti di battimenti (da qui il concetto di purezza e naturalità usato dai musicisti), proprio perché hanno la medesima frequenza. Ad esempio, un intervallo di quinta naturale (3/2) è quindi tale quando il terzo armonico del primo suono del bicordo coincide col secondo armonico dell'altro. E così dicasi per tutti gli innumerevoli intervalli naturali cui Tartini fa ampio riferimento nel suo Trattato.
Esempio:

|
Bicordo la-fa, intervallo di sesta minore. Nell'esempio sonoro prima è eseguito il la, poi il fa, poi il bicordo, con volume crescente. Il terzo suono si percepisce a volume più alto.
Ascoltaⓘ
|
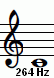
|
Terzo suono risultante dal bicordo precedente, do, una sesta maggiore sotto il la.
Ascoltaⓘ
|
Il fenomeno era già conosciuto almeno dal XVI secolo e veniva sfruttato principalmente nell'arte organaria, in modo da poter dare agli strumenti una maggiore estensione nel basso senza dover costruire canne eccessivamente lunghe e costose. Ad esempio, per ottenere l'effetto di un registro da 32', si suonano contemporaneamente un registro da 16' (ottava) e uno da 10' 2/3 (quinta).
| Intervallo fra le due note |
Rapporto fra le due note |
Terzo suono risultante (in confronto al più grave dei due suoni originari)
|
| Ottava |
1:2 |
Unisono
|
| Quinta |
3:2 |
Ottava inferiore
|
| Quarta |
4:3 |
Dodicesima inferiore
|
| Terza maggiore |
5:4 |
Seconda ottava inferiore
|
| Terza minore |
6:5 |
Seconda ottava inferiore e terza maggiore
|
| Sesta maggiore |
5:3 |
Quinta inferiore
|
| Sesta minore |
8:5 |
Sesta maggiore
|
Bibliografia
- G.Tartini: Trattato di Musica secondo la vera scienza dell'armonia, Stamperia del Seminario, Padova(1754)
- Filippo de' Boni, Biografia degli artisti ovvero dizionario della vita e delle opere dei pittori, degli scultori, degli intagliatori, dei tipografi e dei musici di ogni nazione che fiorirono da' tempi più remoti sino a' nostri giorni, Editore A. Santini e figlio, 1852, p. 997.
- Giuseppe Rovani, Cento anni, Stabilimenti Redaelli, 1868, p. 306.
- Giuseppe Arnaud, Teatro, arte ed artisti: mosaico d'aneddoti di escursioni storiche, schizzi biografici ed artistici, G. Gnocchi di Giacomo Editore, 1869, p. 28.
- Giuseppe Pizzati, La Scienza de Suoni et dell'Armonia, 1782, p. 228.
- Terzo suono, in Dizionario Enciclopedico Universale della Musica e dei Musicisti (diretto da Alberto Basso), Utet, Torino, Il Lessico, Vol. IV, 1984, pp. 532-533
- Enrica Bojan, Introduzione, in Giuseppe Tartini, Trattato di musica secondo la vera scienza dell’armonia, (a cura di Enrica Bojan), Palermo, Novecento editrice, 1996, pp. 5-30
- Giovanni Guanti, Chi ha paura della ‘Scienza platonica fondata nel cerchio’ di Tartini?, in «Rivista Italiana di Musicologia», vol. XXXVIII, n. 1 (2003), pp. 41-73
- C.Bini, G.Lami, I suoni di combinazione ed il terzo suono di Tartini: fisica, storia e musica, Il Campano, Pisa, 2019
Voci correlate
Collegamenti esterni
|
|