Teorema di Ore

Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti.

Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento.

Il teorema di Ore è un teorema della teoria dei grafi provato nel 1960 dal matematico Norvegese Øystein Ore. Fornisce una condizione sufficiente, ma non necessaria, affinché un grafo sia Hamiltoniano, affermando che un grafo che contiene un sufficiente numero di archi, comparati al numero di vertici, deve contenere un ciclo Hamiltoniano. Esso è inoltre una generalizzazione del teorema di Dirac e a sua volta viene generalizzato dal teorema di Bondy-Chvátal.

Enunciato

Sia $G$ un grafo semplice con un numero finito di vertici $n\geq 3$ . Sia $deg(v)$ il grado del vertice $v$ , ossia il numero di archi incidenti su $v$ . Allora il teorema di Ore stabilisce che, presi due vertici $v$ e $w$ non adiacenti, se vale $deg(v)+deg(w)\geq n$ allora $G$ è Hamiltoniano.

Dimostrazione

Usando il teorema di Bondy-Chvátal, la dimostrazione è immediata.

Una possibile dimostrazione diretta è invece la seguente:

Basterà dimostrare che se il grafo non è Hamiltoniano allora la condizione data dal teorema di Ore viene violata. Sia quindi $G$ un grafo privo di cicli hamiltoniani e sia $H$ il grafo ottenuto da $G$ aggiungendo archi fin quando l'aggiunta di un altro arco produrrebbe un ciclo hamiltoniano. Poiché l'aggiunta di un solo arco creerebbe un ciclo hamiltoniano allora necessariamente $H$ possiede un cammino hamiltoniano $(v_{1},v_{2},...,v_{n-1},v_{n})$ , dove gli $n-$ vertici sono stati ordinati in modo tale che l'arco la cui aggiunta creerebbe il ciclo sia $(v_{1},v_{n})$ , che risultano essere quindi due vertici non adiacenti sia in $H$ che in $G$ . Per ogni $2\leq i\leq n$ consideriamo l'arco $(v_{1},v_{i})$ . Se questo arco esiste, ossia se $v_{i}$ fa parte dell'insieme dei vicini di $v_{1}$ , allora necessariamente non deve esistere l'arco $(v_{i-1},v_{n})$ poiché tale arco produrrebbe un ciclo hamiltoniano in $H$ che per ipotesi ne è privo. Infatti un possibile ciclo sarebbe $(v_{1},..,v_{i-1},v_{n},v_{n-1},...,v_{i},v_{1})$ . In conclusione solo uno degli archi $(v_{1},v_{i})$ , $(v_{i-1},v_{n})$ può esistere. Essendo le possibili scelte di $i$ pari a $n-1$ e per ogni $i$ possiamo aggiungere (al più) $v_{i}$ ai vicini di $v_{1}$ escludendo però $v_{i-1}$ ai vicini di $v_{n}$ e viceversa, abbiamo che necessariamente $deg(v_{1})+deg(v_{n})\leq n-1$ . Dunque non viene soddisfatta la condizione posta dal teorema di Ore. Poiché il grado dei vertici in $G$ è minore o al più uguale a quello di $H$ , la condizione del teorema di Ore non viene soddisfatta nemmeno in $G$ .

Corollari

Un corollario del teorema di Ore è il teorema di Dirac che afferma che se per ogni vertice $v$ di un grafo $G$ di $n\geq 3$ vertici, vale $deg(v)\geq {\frac {n}{2}}$ allora $G$ possiede un ciclo hamiltoniano. È immediato vedere che se vale tale relazione per ogni vertice essa vale anche per due vertici $v$ e $w$ non adiacenti e in particolare si ha $deg(v)+deg(w)\geq {\frac {n}{2}}+{\frac {n}{2}}=n$ . La condizione di Ore è quindi soddisfatta.

Bibliografia

Andrian Bondy M. Ram Murty, Graph Theory, Springer, 2011, ISBN 978-1-84628-969-9.

Read other articles:

Kue intil

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Kue intil adalah kue yang berbahan singkong yang ditumbuk bersamaan dengan gula jawa lalu dikukus, setelah matang ditaburi dengan ampas kelapa. Kue tersebut adalah panganan khas Kepulauan Seribu.[1] Referensi ^ Salinan arsip. Diarsipkan dari ve...

Teodora Porfirogênita

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Maio de 2018) Nota: Para outra Teodora Porfirogênita, filha de Constantino VII, veja Teodora (filha de Constantino VII). Para outras pessoas de mesmo nome, veja Teodora. Teodora Porfirogênita Imperatriz e Autocratissa dos Roman...

2020 Georgia House of Representatives election

Not to be confused with 2020 United States House of Representatives elections in Georgia. 2020 Georgia House of Representatives election ← 2018 November 3, 2020 2022 → All 180 seats in the Georgia House of Representatives91 seats needed for a majorityTurnout63.01% 9.02 pp Majority party Minority party Leader David Ralston Bob Trammell(lost re-election) Party Republican Democratic Leader since January 11, 2010 July 24, 2017 Leader's seat 7th 132nd...

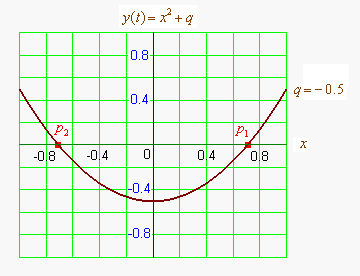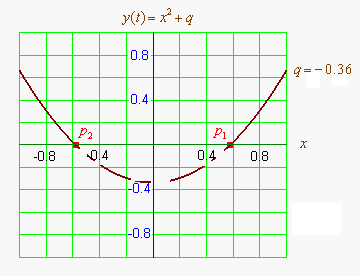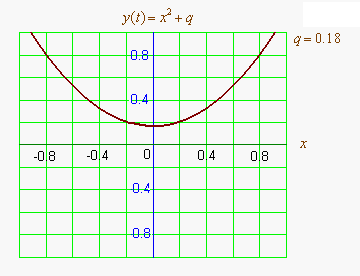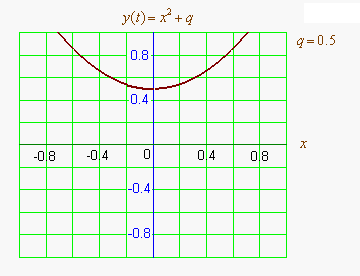
Квадратное уравнение

Квадра́тное уравне́ние — алгебраическое уравнение второй степени с общим видом a x 2 + b x + c = 0 , a ≠ 0 , {\displaystyle ax^{2}+bx+c=0,\;a\neq 0,} в котором x {\displaystyle x} — неизвестное, а коэффициенты a {\displaystyle a} , b {\displaystyle b} и c {\displaystyle c} — вещественные или комплексные числа. Корень уравнения a x 2 + ...

Türkiye 1.Lig 1981-1982

Türkiye 1.Lig 1981-1982 Competizione Türkiye 1.Lig Sport Calcio Edizione 24ª Organizzatore TFF Luogo Turchia Partecipanti 17 Formula Girone unico Sito web tff.org Risultati Vincitore Beşiktaş(6º titolo) Retrocessioni Eskişehirspor Göztepe Diyarbakırspor Statistiche Miglior marcatore Selçuk Yula (15) Incontri disputati 256 Gol segnati 500 (1,95 per incontro) Cronologia della competizione 1980-81 1982-83 Manuale L'edizione 1981-1982 della Türkiy...

Синелобый амазон

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

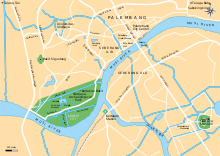
Palembang

City and capital of South Sumatra, Indonesia Not to be confused with Palimbang. For other uses, see Palembang (disambiguation). City in Sumatra, IndonesiaPalembang Pelémbang (Palembang) CityCity of PalembangKota PalembangAmpera BridgeSultan Mahmud Badaruddin II MuseumGateway to the Cheng Ho MosqueSriwijaya Kingdom Archaeological ParkLRT PalembangGreat Mosque of Palembang FlagCoat of armsNicknames: Kota Pempek (City of Pempek)Venetië Van AndalasBumi Sriwijaya (The Land of Srivijaya)Mott...

Air Nostrum

Air NostrumIberia Regional IATA ICAO Kode panggil YW ANE AIR NOSTRUM Didirikan23 May 1994AOC #ES.AOC.002[1]Penghubung Bandar Udara Internasional Barcelona Bandar Udara Internasional Barajas Madrid Bandar Udara Valencia Program penumpang setiaAviosAliansiOneworld (Afiliasi)Armada39[2]Tujuan58[3]Perusahaan indukIberia International Airlines Group (sebagai waralaba dari Iberia) Nefinsa (75%)Caja Duero (22%)Management (3%)Kantor pusatValencia, Wilayah Valencia, SpanyolPend...

Darius the Great

Persian ruler from 522 to 486 BCE Darius the Great𐎭𐎠𐎼𐎹𐎺𐎢𐏁King of KingsGreat KingKing of PersiaKing of BabylonPharaoh of EgyptKing of CountriesThe relief stone of Darius the Great in the Behistun InscriptionKing of Kings of the Achaemenid EmpireReign29 September 522 BCE – October 486 BCECoronationPasargadaePredecessorBardiyaSuccessorXerxes IPharaoh of EgyptReignSeptember 522 BCE – October 486 BCEPredecessorBardiyaSuccessorXerxes I Royal titulary Horus name mnḫ-jbMene...

Gerald M. Edelman

Gerald Maurice EdelmanGerald M. Edelman, 2010.LahirGerald Maurice Edelman(1929-07-01)1 Juli 1929Ozone Park, Queens, New YorkMeninggal17 Mei 2014(2014-05-17) (umur 84)[1]La Jolla, CaliforniaKebangsaanAmerika SerikatDikenal atassistem kekebalanPenghargaanPenghargaan Nobel dalam Fisiologi atau Kedokteran tahun 1972Karier ilmiahBidangimunologi Gerald Maurice Edelman (1 Juli 1929 – 17 Mei 2014) adalah ilmuwan Amerika Serikat. Edelman memenangkan Penghargaan Nobel dala...

Yevgeni Konovalov

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada September 2016. Yevgeni KonovalovInformasi pribadiNama lengkap Yevgeni Sergeyevich KonovalovTanggal lahir 26 September 1988 (umur 35)Tinggi 1,76 m (5 ft 9+1⁄2 in)Posisi bermain Penjaga gawangInformasi klubKlub saat ini Tidak terikatKarier s...

Province of Guadalajara

Province of Spain This article is about the province of Guadalajara in Spain. For other uses, see Guadalajara (disambiguation). Province in Castilla–La Mancha, SpainGuadalajaraProvince FlagCoat of armsMap of Spain with Guadalajara highlightedCoordinates: 40°50′N 2°30′W / 40.833°N 2.500°W / 40.833; -2.500CountrySpainAutonomous communityCastilla–La ManchaCapitalGuadalajaraArea • Total12,167 km2 (4,698 sq mi) • RankRanked...

São Tomás de Aquino

Questa voce sull'argomento centri abitati del Minas Gerais è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. São Tomás de Aquinocomune LocalizzazioneStato Brasile Stato federato Minas Gerais MesoregioneSul e Sudoeste de Minas MicroregioneSão Sebastião do Paraíso AmministrazioneSindacoRoneido Teofilo de Carvalho TerritorioCoordinate20°46′57″S 47°05′49″W / 20.7825°S...

Sea change (idiom)

English idiomatic expression Sea change or sea-change is an English idiomatic expression that denotes a substantial change in perspective, especially one that affects a group or society at large, on a particular issue. It is similar in usage and meaning to a paradigm shift, and may be viewed as a change to a society or community's zeitgeist, with regard to a specific issue. The phrase evolved from an older and more literal usage when the term referred to an actual change wrought by the sea,&#...

Wolverine (Amtrak train)

Amtrak service between Chicago, IL, and Pontiac, MI This article is about the current Amtrak service. For the historic train through Ontario and Buffalo, see Wolverine (NYC train). WolverineThe Wolverine at Royal Oak station in March 2011OverviewService typeHigher-speed inter-city railLocaleMidwestern United StatesFirst serviceMay 1, 1971Current operator(s)AmtrakFormer operator(s)Penn CentralAnnual ridership420,569 (FY23) 14.5%[a][1]RouteTerminiChicago, IllinoisPontiac, Michig...

Pipe rolls

Medieval and post-medieval English financial documents Pipe rollsExtract from the 1194 Pipe rollLanguageMedieval Latin, Middle English, EnglishDate1129–1833ProvenanceEnglish ExchequerExchequer of IrelandSeriesPipe rollsGenreAccounting documentsSubjectRecords of the audits of the English Exchequer and Exchequer of IrelandPeriod covered1130–1833 The Pipe rolls, sometimes called the Great rolls[1] or the Great Rolls of the Pipe, are a collection of financial records maintained by the...

Université de Californie à Berkeley

Université de Californie à BerkeleyHistoireFondation 23 mars 1868 (156 ans)StatutType Université publiqueNom officiel University of California, BerkeleyRégime linguistique Anglais américainPrésident Carol T. Christ (en)Devise Fiat lux (latin) Let There Be Light (anglais) (« Que la lumière soit »)Membre de Université de CalifornieSite web www.berkeley.eduChiffres-clésÉtudiants 45 057 (2021)[4]Effectif 12 122 (2020)Enseignants 2 132 (2021)[4]Budget...

قانون نقل المواد الخطرة

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يوليو 2020) قانون نقل المواد الخطرةمعلومات عامةالبداية 30 سبتمبر 1957[1][2] جانب من جوانب نقل بري الاسم الرسمي Accord européen relatif au transport international des marchandises Dangereuses par Route (بال�...

Oil paint

Type of slow-drying paint View of Delft in oil paint, by Johannes Vermeer. Oil paint is a type of slow-drying paint that consists of particles of pigment suspended in a drying oil, commonly linseed oil. For several centuries the oil painting has been perhaps the most prestigous form in Western art, but oil paint has many practical uses, mainly because it is waterproof. The earliest surviving examples of oil paint have been found in Asia from as early as the 7th century AD, in examples of Budd...

Ted Marchibroda

American football player and coach (1931–2016) American football player Ted MarchibrodaMarchibroda in 1996No. 17, 18, 7Position:QuarterbackPersonal informationBorn:(1931-03-15)March 15, 1931Franklin, Pennsylvania, U.S.Died:January 16, 2016(2016-01-16) (aged 84)Weems, Virginia, U.S.Career informationCollege:St. BonaventureDetroitNFL draft:1953 / Round: 1 / Pick: 5Career history As a player: Pittsburgh Steelers (1953, 1955–1956) Chicago Cardinals (1957) As a coach: ...