Taglio (teoria dei grafi)
|
Read other articles:

Para pedagang derivatif di Chicago Board of Trade. Bursa berjangka adalah tempat atau fasilitas memperjualbelikan kontrak atas sejumlah komoditas atau instrumen keuangan dengan harga tertentu yang penyerahan barangnya disepakati akan dilakukan pada saat yang akan datang. Bursa berjangka juga diartikan pertukaran keuangan pusat di mana orang dapat memperdagangkan kontrak berjangka sesuai standar yang ditentukan oleh bursa.[1] Kontrak itu dibuat antara pihak-pihak yang saling tidak tahu...

American military officer and planter (1742-1786) This article is about the American Revolutionary War general. For other people with a similar name, see Nathaniel Greene. Nathanael Greene1792 portrait of Greene by John TrumbullNickname(s)The Savior of the South The Fighting QuakerBornAugust 7 [O.S. July 27] 1742Colony of Rhode Island and Providence Plantations, British AmericaDiedJune 19, 1786(1786-06-19) (aged 43)Mulberry Grove, Georgia, United StatesBuriedSavannah, G...

One Missed CallTheatrical release posterSutradaraEric ValetteProduserScott KroopfBroderick JohnsonDitulis olehAndrew KlavanPemeranEdward BurnsShannyn SossamonPenata musikReinhold HeilJohnny KlimekSinematograferGlen MacPhersonPenyuntingSteve MirkovichDistributorWarner Bros.Tanggal rilis4 Januari 2008Durasi87 menitNegaraAmerika SerikatBahasaInggrisAnggaran$20 MillionPendapatankotor$30,192,235IMDbInformasi di IMDbAMGProfil All Movie GuideSitus webhttp://onemissedcallmovie.warnerbros.com/ O...

Halaman ini berisi artikel tentang kota. Untuk kabupaten bernama sama, lihat Malang. Untuk kegunaan lain, lihat Malang (disambiguasi). Koordinat: 7°58′37.5″S 112°38′02.6″E / 7.977083°S 112.634056°E / -7.977083; 112.634056 Kota MalangKotaTranskripsi bahasa daerah • Hanacarakaꦩꦭꦁ • Abjad Pegonمالاڠ • Osob KiwalanNgalamSearah jarum jam, dari kiri atas: Balai Kota Malang dan Monumen Tugu, Candi Badut, Stadion ...

Penghargaan Filmfare untuk Aktris Pendukung TerbaikDeskripsiPenampilan Terbaik dari seorang Aktris dalam sebuah Peran PendukungNegaraIndiaDipersembahkan olehFilmfareDiberikan perdana1954Pemegang gelar saat iniTabu, Haider (2014)Situs webFilmfare Awards Penghargaan Filmfare untuk Aktris Pendukung Terbaik diberikan oleh Filmfare sebagai bagian dari Penghargaan Filmfare tahunannya untuk film-film Hindi, untuk menghargai seorang aktor perempuan yang memberikan penampilan menarik dalam sebuah pera...

Manu Sánchez Nazionalità Spagna Altezza 179 cm Peso 70 kg Calcio Ruolo Difensore Squadra Celta Vigo Carriera Giovanili 201?-2014 Cornellà2014-2019 Atlético Madrid Squadre di club1 2019-2020 Atlético Madrid B29 (0)[1]2019-2021 Atlético Madrid6 (0)2021-2023→ Osasuna80 (1)2023- Celta Vigo17 (0) Nazionale 2020- Spagna U-216 (2) Palmarès Europei di calcio Under-21 Argento Romania-Georgia 2023 1 I due numeri indicano le presenze e l...

Calaucittà Calau – Veduta LocalizzazioneStato Germania Land Brandeburgo DistrettoNon presente CircondarioOberspreewald-Lusazia TerritorioCoordinate51°44′48.55″N 13°56′57.88″E / 51.746819°N 13.949411°E51.746819; 13.949411Coordinate: 51°44′48.55″N 13°56′57.88″E / 51.746819°N 13.949411°E51.746819; 13.949411 Altitudine93 m s.l.m. Superficie163,5 km² Abitanti7 660[1] (31-12-2022) Densità46,85 ab./km² ...

Géraud Ier de MâconTitre de noblesseComteBiographieNaissance 1124MâconDécès 15 septembre 1184Famille Maison d'IvréePère Guillaume IV de BourgogneMère Poncette de Traves (d)Fratrie Étienne I d'AuxonneConjoint Maurette de Salins (d) (à partir de 1160)Enfants Gaucher IV de MâconGuillaume IV de MâconBéatrice de VienneAlexandrine de Vienne (d)Ida de Vienne (d)modifier - modifier le code - modifier Wikidata Géraud Ier de Mâcon (prénom que retrouve auss...

Placoderm fish from the late Ludlow epoch of the Silurian period Entelognathus primordialisTemporal range: 424–419 Ma PreꞒ Ꞓ O S D C P T J K Pg N ↓ Late Silurian Holotype, Paleozoological Museum of China Life reconstruction of Entelognathus primordialis Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: †Placodermi Order: †incertae sedis Genus: †EntelognathusZhu et al., 2013 [1] Species: †E. primordialis Binomial nam...

Canadian English-language specialty channel Television channel DTourDTour logoCountryCanadaBroadcast areaNationwideHeadquartersToronto, Ontario, CanadaProgrammingPicture format480i (SDTV)1080i (HDTV)OwnershipOwnerCanwest(1997–2010)Shaw Media(2010–2016)Corus Entertainment(2016–present)ParentTVTropolis G.P.Sister channelsHGTVFood NetworkOWNW NetworkSliceNational GeographicNat Geo WildMagnolia NetworkCooking ChannelHistoryShowcaseHistoryLaunchedOctober 17, 1997; 26 years ago (...
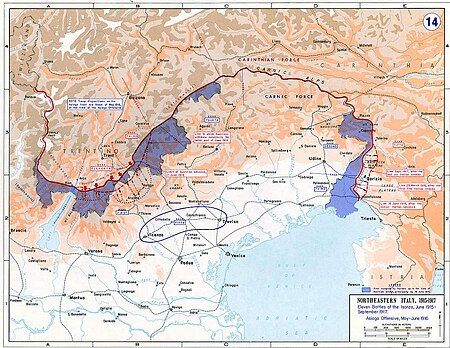
A mine gallery in the ice at Pasubio The Italian front in 1915–1917, initial Italian conquests shown in blue The mines on the Italian front during the First World War comprised a series of underground explosive charges of varying sizes, secretly planted between 1916 and 1918 by Austro-Hungarian and Italian tunneling units beneath their enemy's lines along the Italian front in the Dolomite section of the Alps. Background From 1915, the high peaks of the Dolomites range were an area of fierce...

François Pierre-AlypeFonctionsPréfet de la Girondeaoût 1940 - mai 1942Marcel Bodenan (d)Maurice SabatierPréfet de la Charente-Maritime26 novembre 1939 - 6 août 1940Gouverneur de la Guadeloupe29 novembre 1938 - 26 janvier 1940Léopold Arthur André Allys (d)Georges Venard (d)Gouverneur de la Côte française des Somalis (intérim)15 juin 1937 - 30 mai 1938Hubert DeschampsBiographieNaissance 13 avril 1886Saint-Denis (La Réunion, France)Décès 5 février 1956 (à 69 ans)Suresnes (Sei...

Computer instruction set architecture Power ISADesignerPower.orgOpenPOWER FoundationBits32-bit/64-bit (32 → 64)Introduced2006; 18 years ago (2006)Version3.1DesignRISCTypeLoad–storeEncodingFixed/VariableBranchingCondition codeEndiannessBig/BiExtensionsAltiVec, PowerPC AS, APU, DSP, CBEAOpenYes, and royalty freeRegisters 32× 64/32-bit general-purpose registers 32× 64-bit floating-point registers 64× 128-bit vector registers 32-bit condition code register 32-bit link reg...

Florian Vogel Datos personalesNacimiento Aarau, Suiza18 de febrero de 1982 (42 años)Carrera deportivaRepresentante de Suiza SuizaDeporte Ciclismo de montaña Medallero Ciclismo de montaña masculino Evento O P B Campeonato Mundial 2 4 3 Campeonato Europeo 4 3 1 [editar datos en Wikidata] Florian Vogel (Aarau, 18 de febrero de 1982) es un deportista suizo que compitió en ciclismo de monta�...

2023 French Polynesian legislative election ← 2018 16 April 2023 (first round)30 April 2023 (second round) 2028 → All 57 seats in the Assembly of French Polynesia29 seats needed for a majorityTurnout60.08% (first round) 1.43pp 69.96% (second round) 3.14pp Party Leader % Seats +/– Tāvini Huiraʻatira Oscar Temaru 44.32 38 +30 Tāpura–ʻĀmuitahiraʻa Édouard Fritch 38.53 16 −33 A here ia Porinetia Nuihau Laurey 17.16 3 New This lists parties that won seats. See t...

Large gravitationally bound system of stars and interstellar matter This article is about the astronomical structure. For Earth's galaxy, see Milky Way. For other uses, see Galaxy (disambiguation). NGC 4414, a typical spiral galaxy in the constellation Coma Berenices, is about 55,000 light-years in diameter and approximately 60 million light-years from Earth. A galaxy is a system of stars, stellar remnants, interstellar gas, dust, and dark matter bound together by gravity.[1][...
Para el oidor y alcalde mayor de Yucatán en 1560-1562, véase Jofre de Loayza. García Jofre de LoaísaInformación personalNombre en español García Jofré de Loayza Nacimiento 1490 Ciudad Real (España) Fallecimiento 30 de julio de 1526jul. océano Pacífico Nacionalidad EspañolaInformación profesionalOcupación Explorador y marino [editar datos en Wikidata] Francisco José García Jofre de Loaísa o García Jofré de Loaisa o Loaysa o Loayza (Ciudad Real, 1490[cita requ...

Market town in Derbyshire, England This article is about the town in Derbyshire, England. For other uses, see Bakewell (disambiguation). Human settlement in EnglandBakewellBakewell town centreBakewell parish highlighted within DerbyshirePopulation3,949 [1]OS grid referenceSK2168Civil parishBakewellDistrictDerbyshire DalesShire countyDerbyshireRegionEast MidlandsCountryEnglandSovereign stateUnited KingdomPost townBAKEWELLPostcode districtDE45Dialling ...

Village in Devon, England Human settlement in EnglandWidecombe in the MoorVillage greenWidecombe in the MoorLocation within DevonOS grid referenceSX718767Civil parishWidecombe in the Moor[1]DistrictTeignbridgeShire countyDevonRegionSouth WestCountryEnglandSovereign stateUnited KingdomPost townNEWTON ABBOTPostcode districtTQ13Dialling code01364PoliceDevon and CornwallFireDevon and SomersetAmbulanceSouth Western UK ParliamentCentral DevonWebsiteThe Wid...

Self-guided improvement For other uses, see Self-help (disambiguation). A self-help group from Maharashtra making a demonstration at a National Rural Livelihood Mission seminar held at Chandrapur Self-help or self-improvement is a self-directed improvement of oneself[1]—economically, physically, intellectually, or emotionally—often with a substantial psychological basis. When engaged in self-help, people often use publicly available information, or support groups—on the Internet...








