Rischio di credito
|
Read other articles:

Le siège de la Réserve fédérale à Washington, DC La banque centrale est une institution financière publique chargée par l'État de conduire la politique monétaire du pays ou de sa zone économique. Elle est régie par un mandat qui précise ses objectifs, tels que la stabilité des prix, la confiance en la monnaie, la stabilité financière ou encore le plein emploi. Une banque centrale peut être indépendante du pouvoir politique. Définition Une banque centrale est une institution ...

Le Los Angeles Convention Center pendant l'E3 2013. L’Electronic Entertainment Expo 2013, communément appelé E3 2013, est la 19e édition d'un salon consacré exclusivement aux jeux vidéo organisé par l'Entertainment Software Association. L'événement s'est déroulé du 11 au 13 juin 2013 au Los Angeles Convention Center à Los Angeles[1]. Bien que dévoilées tour à tour par Sony et par Microsoft avant la tenue du salon, cette édition est marquée par la présentation au public...

Nikko NatividadNatividad pada tahun 2017LahirNicholai Seagal Natividad13 Februari 1993 (umur 31)Malolos, Bulacan, FilipinaPekerjaanModel, pemeran, penariTahun aktif2014–sekarangAgenStar Magic(2014–2022) Viva Artists Agency (2022–present)Dikenal atasNikko, #NikkoTinggi170 m (557 ft 9 in)Suami/istriCielo Mae Eusebio (m. 2021)Anak1 Nicholai Seagal Natividad (lahir 13 Februari 1993) adalah model, pemeran, dan penari Filipina, yang men...

Douglas DC-2 DC-2 PH-AJU came second in the MacRobertson Air Race Jenis Passenger & military transport Pembuat Douglas Aircraft Company, Fokker Penerbangan perdana 11 Mei, 1934 Diperkenalkan 18 Mei, 1934 Pengguna utama United StatesAustraliaGermanyUnited Kingdom Jumlah 156 Dikembangkan dari Douglas DC-1 Varian Douglas DC-3 Douglas DC-2 adalah pesawat berkipas sayap rendah (low wing) yang diproduksi oleh Douglas Aircraft Company pada 1930-an. Pesaing utamanya saat itu adalah Boeing 2...

Konstantin Rokossovsky nama penuh Konstantin Konstantinovich Rokossovsky (1896-1968), Ia adalah seorang komandan militer Soviet terkenal karena perannya dalam pertempuran Stalingrad (194201943) Konstantin Rokossovsky nama penuh Konstantin Konstantinovich Rokossovsky (lahir, 21 Desember [ 9 Desember, penemuan baru] 1896 di Velikiye Luki, Rusia - meninggal, 3 Agustus 1968 di Moscow) adalah seorang komandan militer Soviet yang terkenal karena perannya dalam Pertempuran Stalingrad (1942-1943). ...

Сибирский горный козёл Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКла�...

豪栄道 豪太郎 場所入りする豪栄道基礎情報四股名 澤井 豪太郎→豪栄道 豪太郎本名 澤井 豪太郎愛称 ゴウタロウ、豪ちゃん、GAD[1][2]生年月日 (1986-04-06) 1986年4月6日(38歳)出身 大阪府寝屋川市身長 183cm体重 160kgBMI 47.26所属部屋 境川部屋得意技 右四つ・出し投げ・切り返し・外掛け・首投げ・右下手投げ成績現在の番付 引退最高位 東大関生涯戦歴 696勝493敗...

This article is about the mountain range. For the associated ecoregion, see Klamath Mountains (ecoregion). Mountain range in Oregon and California, United States Klamath MountainsMixed conifer forest in the Trinity AlpsHighest pointPeakMount EddyElevation9,025 ft (2,751 m)ListingMountains of OregonMountains of CaliforniaDimensionsLength249 km (155 mi)[1]Width181 km (112 mi)[1]Area25,595 km2 (9,882 sq mi)[1]GeographyMap ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) دوري جزر المالديف لكرة القدم 2010 تفاصيل الموسم دوري جزر المالديف لكرة القدم [لغات أخرى] البلد...

佩德羅特謝拉Pedro Teixeira市鎮奧拉里亞在巴西北里約格朗德州的位置坐标:21°43′S 43°44′W / 21.717°S 43.733°W / -21.717; -43.733國家 巴西分區巴西東南部州米納斯吉拉斯州 佩德羅特謝拉(葡萄牙語:Pedro Teixeira)是巴西的城鎮,位於該國東南部,由米納斯吉拉斯州負責管轄,始建於1963年3月1日,面積113平方公里,2010年人口1,789,人口密度每平方公里15.82人。 �...

Beijing Subway station Fengbo俸伯PlatformGeneral informationLocationShunyi District, BeijingChinaCoordinates40°07′57″N 116°41′05″E / 40.1326°N 116.6847°E / 40.1326; 116.6847Operated byBeijing Mass Transit Railway Operation Corporation LimitedLine(s) Line 15Platforms2 (1 island platform)Tracks2ConstructionStructure typeUndergroundAccessibleYesHistoryOpenedDecember 31, 2011; 12 years ago (2011-12-31)Services Pr...

Radio station in Lost Hills–Bakersfield, California KEBTLost Hills, CaliforniaBroadcast areaBakersfield, CaliforniaFrequency96.9 MHzBrandingLa Caliente 96.9ProgrammingFormatRegional MexicanOwnershipOwnerAmerican General MediaSister stationsKERN, KGEO, KGFM, KISV, KKXX-FMHistoryFirst air date1996 (as KWQH)Former call signsKWQH (1990–2001)KLRM (2001–2006)[1]Call sign meaningBeat (previous branding)Technical information[2]Licensing authorityFCCFacility ID11622ClassB1ERP15,5...
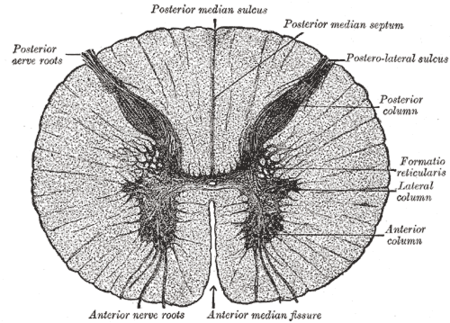
Anterior median fissure of spinal cordA spinal nerve with its anterior and posterior roots.Transverse section of the spinal cord in the mid-thoracic region.DetailsIdentifiersLatinfissura mediana anterior medullae spinalisTA98A14.1.02.007TA26053FMA83735Anatomical terminology[edit on Wikidata] The anterior median fissure of the spinal cord is a deep midline groove of the anterior/ventral spinal cord.[1]: 486 It divides the white matter of the anterior spinal cord ne...

Roman construction, Gallic Wars Caesar's Rhine Bridge, an 1814 portrait by John Soane The Italian cross-section of the bridge Reconstruction in Koblenz of a Roman pile driver, used to build the Rhine bridges Caesar's bridges across the Rhine, the first two bridges on record to cross the Rhine river, were built by Julius Caesar and his legionaries during the Gallic War in 55 BC and 53 BC. Strategically successful, they are also considered masterpieces of military engineering.[1] Backgr...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字(Microsoftコードページ932(はしご高))が含まれています(詳細)。 火口のふたり著者 白石一文発行日 2012年11月12日発行元 河出書房新社ジャンル 恋愛小説官能小説国 日本言語 日本語形態 四六判ページ数 232公式サイト kawade.co.jpコード ISBN 978-4-309-02142-3 ISBN 978-4-309-41375-4(文庫本) ウィキポータル �...

Rinieri della SassettaRinieri in un dipinto di Rosso FiorentinoSignore di SassettaStemma Nome completoRinieri Orlandi della Sassetta MorteCerbaia in Val di Pesa, 25 agosto 1520 DinastiaOrlandi PadrePietro Paolo della Sassetta MadreMattea Fei FigliFabio ReligioneCattolicesimo Rinieri della SassettaCause della morteDecapitazione Etniaitaliana Dati militariPaese servito Repubblica fiorentina Repubblica di Venezia Regno di Napoli Sacro Romano Impero Stato Pontificio CorpoCavaller...

Vector field describing the density of electric dipole moments in a dielectric material Articles aboutElectromagnetism Electricity Magnetism Optics History Computational Textbooks Phenomena Electrostatics Charge density Conductor Coulomb law Electret Electric charge Electric dipole Electric field Electric flux Electric potential Electrostatic discharge Electrostatic induction Gauss law Insulator Permittivity Polarization Potential energy Static electricity Triboelectricity Magnetostatics Amp�...

Ėrnesto InarkievNazionalità Russia Scacchi CategoriaGrande maestro internazionale Ranking81º (agosto 2023), 2658 p. Elo Best ranking25º (ottobre 2016) Record Miglior Elo 2732 (settembre 2016) Palmarès Competizione Ori Argenti Bronzi Campionati europei 1 0 0 Campionati russi 0 0 1 Vedi maggiori dettagli Modifica dati su Wikidata · Manuale Ėrnesto Inarkiev (in russo Эрнесто Инаркиев?; Regione di Oš, 9 dicembre 1985) è uno scacchista russo, Gran...

Milos RaonicMilos Raonic all'US Open 2016Nazionalità Canada Altezza196[1] cm Peso98[1] kg Tennis Carriera Singolare1 Vittorie/sconfitte 383-184 (67.55%) Titoli vinti 8 Miglior ranking 3º (21 novembre 2016) Ranking attuale ranking Risultati nei tornei del Grande Slam Australian Open SF (2016) Roland Garros QF (2014) Wimbledon F (2016) US Open 4T (2012, 2013, 2014, 2018) Altri tornei Tour Finals SF (2016) Giochi olimpici 2T (2012) Doppi...

Municipality and town in Zeeland, NetherlandsVeere Ter Veere (Zeeuws)Municipality and townThe city of Veere in 2007 FlagCoat of armsLocation in ZeelandCoordinates: 51°32′53″N 3°40′00″E / 51.54806°N 3.66667°E / 51.54806; 3.66667CountryNetherlandsProvinceZeelandGovernment[1] • BodyMunicipal council • MayorFrederiek Schouwenaar (VVD)Area[2] • Total206.55 km2 (79.75 sq mi) • La...