Principio di minimo vincolo
|
Read other articles:

Bupati BungoLambang Kabupaten BungoPetahanaH. Mashuri, S.P., M.E.sejak 14 Juni 2021KediamanPendapa Kabupaten BungoMasa jabatan5 tahunDibentuk1965Pejabat pertamaM. SaidiSitus webwww.bungokab.go.id Berikut ini adalah daftar Bupati Bungo dari masa ke masa.[1] No Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Wakil Bupati 1 M. Saidi 12 September 1965 1968 1 [Ket. 1] 2 H.Hoessin Saad 1968 1975 2 3 Drs. H.Hasan 1975 1986 3 4 Drs. H.Abdul MutholibHs 1986 1996 4 5 Drs. H.Syofyan Al...
Administrative entry restrictions Not to be confused with Visa policy of Tuvalu. A Tuvaluan passport Visa requirements for Tuvaluan citizens are administrative entry restrictions by the authorities of other states placed on citizens of Tuvalu. As of 20 December 2020, Tuvaluan citizens had visa-free or visa on arrival access to 127 countries and territories, ranking the Tuvaluan passport 45th in terms of travel freedom (tied with passport of Colombia) according to the Henley Passport Index. ...

Mattakkalappu Maanmiyam Mattakallappu Manmiyam cover pageAuthorF. X. NadarajahOriginal titleமட்டக்களப்பு மான்மியம்CountrySri LankaLanguageTamilGenreHistoryPublisherBatticaloa District Cultural BoardPublication date1962PagesXII + 128 + 9 Mattakkalappu Maanmiyam (Tamil: மட்டக்களப்பு மான்மியம்; The Glory of Batticaloa) is a Tamil language historical book concerning the history of Batticaloa.[1] It w...

Sabah Al-Ahmad Al-Jaber Al-SabahSabah IV in 2018Emir KuwaitBerkuasa29 Januari 2006 –29 September 2020PendahuluSaad Al-SalimPenerusNawaf Al-Ahmad Al-JaberInformasi pribadiKelahiran(1929-06-16)16 Juni 1929Jahra Syekh Kuwait[1]Kematian29 September 2020(2020-09-29) (umur 91)Rochester, Minnesota, A.S.Pemakaman30 September 2020Pemakaman Sulaibikhat[2]WangsaSabahAyahAhmad Al-Jaber Al-SabahIbuMunira Othman Hamad Al-Ayyar Al-SaeedPasanganSheikha Fatuwah Salman Al-Sabah (meningga...

Partizan NISJulukanParni Valjak Crno-BeliLigaLiga Bola Basket SerbiaLiga ABADibentuk1945SejarahKK Partizan(1945–sekarang)ArenaBalai Aleksandar NikolićKapasitas5.878[1]LetakBeograd, SerbiaWarna timHitam dan putih Sponsor utamaNaftna Industrija SrbijePresidenOstoja MijailovićJuara1 EuroLeague3 Piala Korać6 Liga ABA21 Kejuaraan Nasional14 Piala NasionalSitus webwww.kkpartizan.rs Kandang Tandang Košarkaški klub Partizan (bahasa Serbia: Кошаркашки клуб ...

Voce principale: Football Club Bari 1908. Associazione Sportiva BariStagione 2013-2014Sport calcio Squadra Bari AllenatoreCarmine Gautieri (ritiro pre-campionato) Roberto Alberti Mazzaferro Presidente Francesco Vinella (dimesso) Gianluca Paparesta (subentrato) Serie B7º Play-offSemifinalista Coppa ItaliaTerzo turno Maggiori presenzeCampionato: Guarna, Galano (41)Totale: Guarna, Galano (42) Miglior marcatoreCampionato: Galano (11)Totale: Galano (11) StadioSan Nicola (58 270) Maggio...

Ini adalah nama Batak Toba, marganya adalah Siagian. Bachtiar SiagianLahir(1923-02-19)19 Februari 1923Binjai, Sumatera UtaraMeninggal19 Maret 2002(2002-03-19) (umur 79)JakartaPekerjaanSutradara, penulis skenarioSuami/istriYeni PrastantiAnakIndra Porhas Siagian Bunga Pratiwi Siagian Bismar Siagian Bachtiar Siagian (19 Februari 1923 – 19 Maret 2002)[1] adalah seorang sutradara dan penulis skenario asal Indonesia. Ia pernah meraih Piala FFI sebagai Sutradara Terbaik ...

Mister FantasticMister Fantastic, disegnato da Alex Ross UniversoUniverso Marvel AutoriStan Lee Jack Kirby EditoreMarvel Comics 1ª app.novembre 1961 1ª app. inFantastic Four n. 1 Editore it.Giovanni Gandini Editore 1ª app. it.giugno 1966 1ª app. it. inLinus Estate supplemento al n. 15 di linus Caratteristiche immaginarieAlter egoReed Richards SpecieUmano mutato SessoMaschio Poteri Intelletto di livello geniale Ingegnere, fisico, biologo e chimico eccezionale Elasticità, ...

Disambiguazione – Se stai cercando il cestista argentino, vedi Franco Giorgetti (cestista). Questa voce o sezione sull'argomento ciclisti italiani non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Franco Giorgetti Nazionalità Italia Ciclismo Specialità Pista, strada Termine carriera 1943 CarrieraS...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

A Christmas Carol Sampul edisi pertama (1843)PengarangCharles DickensJudul asliA Christmas Carol. In Prose. Being a Ghost Story of Christmas.IlustratorJohn LeechNegaraInggrisDiterbitkan19 Desember 1843PenerbitChapman & HallTeksA Christmas Carol di Wikisource A Christmas Carol. In Prose. Being a Ghost Story of Christmas, atau yang lebih dikenal dengan A Christmas Carol, merupakan novela yang dikarang oleh Charles Dickens. Edisi pertama novela ini diterbitkan oleh Chapman & Hall di...

عبد الرحمن بن ملجم معلومات شخصية الوفاة 28 يناير 661الكوفة سبب الوفاة قطع الرأس مواطنة الخلافة الراشدة الديانة الإسلام، خوارج الحياة العملية المهنة فارس ومحارب ومعلم قرآن تهم التهم قتل علي بن أبي طالب العقوبة القصاص الدافع انتقامًا لقتلى الخوارج في معركة النه...

Genus of conifers TaiwaniaTemporal range: Albian–Recent PreꞒ Ꞓ O S D C P T J K Pg N Conservation status Vulnerable (IUCN 3.1)[1] Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Gymnospermae Division: Pinophyta Class: Pinopsida Order: Cupressales Family: Cupressaceae Subfamily: Taiwanioideae Genus: TaiwaniaHayata Species: T. cryptomerioides Binomial name Taiwania cryptomerioidesHayata Synonyms[2] Eotaiwania Y.Yendo Taiwania flousiana Gaus...

British scientist This article is about the British zoologist. For the Governor of Madras, see Francis Day (Madras). For the American artist, see Francis Day (artist). For the British actress whose name has a similar spelling, see Frances Day. For the British music publishers, see Francis, Day & Hunter Ltd. Francis Day Francis Talbot Day CIE (2 March 1829 – 10 July 1889) was an army surgeon and naturalist in the Madras Presidency who later became the Inspector-General of Fisheries in In...

Sharp PC-1251Sharp PC-1251ManufacturerSharp CorporationGenerationFirstRelease date1982 (1982)Memory4 Kbit RAM modulesDisplay24 digit dot matrix LCDInputFull QWERTY-style keyboardPower2 built-in batteriesSuccessorSharp PC-5000RelatedSharp PC-1211Sharp PC-1500 The Sharp PC-1251 was a small pocket computer that was also marketed as the Tandy Pocket Computer. It was created by Sharp Corporation in 1982.[1] Technical specifications PC-1251, with its printer and microcassette reco...

American businessman Fred HarveyBornFrederick Henry Harvey(1835-06-27)June 27, 1835London, England, United KingdomDiedFebruary 9, 1901(1901-02-09) (aged 65)Leavenworth, Leavenworth County, Kansas, US Frederick Henry Harvey (June 27, 1835 – February 9, 1901) was an entrepreneur who developed the Harvey House lunch rooms, restaurants, souvenir shops, and hotels, which served rail passengers on the Atchison, Topeka and Santa Fe Railway, the Gulf Colorado and Santa Fe Railway, the Kansas P...
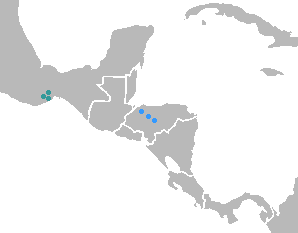
Proposed language family Tolatecan(abandoned)GeographicdistributionMesoamericaLinguistic classificationProposed language familySubdivisions Tequistlatecan (Chontal) Tolan GlottologNone Tolatecan is a proposal by Campbell and Oltrogge (1980) linking two language families of Mesoamerica, Tequistlatecan (Chontal of Oaxaca) and Tol/Jicaque languages of Honduras.[1] Later, Campbell (1997) said that Tolatecan is not likely to be a valid language family.[2] Vocabulary Below is a comp...

Association football club in Stoke-on-Trent, England Football clubPort ValeFull namePort Vale Football ClubNickname(s)The Valiants[1]Short nameVale, PVFCFounded1876; 148 years ago (1876) (disputed)[2][a]1879; 145 years ago (1879) (speculated)[4]1907; 117 years ago (1907) (reestablished)[3]GroundVale Park, Burslem, Stoke-on-TrentCapacity15,036[5]Coordinates53°2′59″N 2°11′33″W...

Swimmingat the Games of the XXV OlympiadPiscines Bernat PicornellVenuePiscines Bernat PicornellDates26 – 31 July 1992No. of events31Competitors641 from 92 nations← 19881996 → Swimming at the1992 Summer OlympicsFreestyle50 mmenwomen100 mmenwomen200 mmenwomen400 mmenwomen800 mwomen1500 mmenBackstroke100 mmenwomen200 mmenwomenBreaststroke100 mmenwomen200 mmenwomenButterfly100 mmenwomen200 mmenwomenIndividual medley200 mmenwomen400 mmenwomenFreestyle relay4 × 1...

الرابطة التونسية للدفاع عن حقوق الإنسان البلد تونس تاريخ التأسيس 1976 تعديل مصدري - تعديل شعار الرابطة التونسية للدفاع عن حقوق الإنسان الرابطة التونسية للدفاع عن حقوق الإنسان هي المنظمة الحقوقية الرئيسية في تونس. تأسست الرابطة التونسية للدفاع عن حقوق الإنسان في 7...








































![{\displaystyle \mathbf {K} =\mathbf {M} ^{1/2}\left[\mathbf {I} -\left(\mathbf {A} \mathbf {M} ^{-1/2}\right)^{+}\mathbf {A} \mathbf {M} ^{-1/2}\right]\mathbf {M} ^{-1/2}\mathbf {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffb4fefba9ac55e96e8c6f8b36e54f3b0166e8a1)








![{\displaystyle {\begin{aligned}&\mathbf {Q} _{c^{\prime }}=\mathbf {M} _{\mathbf {A} }^{1/2}\left(\mathbf {A} \mathbf {M} _{\mathbf {A} }^{-1/2}\right)^{+}\left(\mathbf {b} -\mathbf {A} \mathbf {M} _{\mathbf {A} }^{-1}\mathbf {Q} _{\mathbf {b} }\right)+\mathbf {K} _{\mathbf {A} }\\&\mathbf {K} _{\mathbf {A} }=\mathbf {M} _{\mathbf {A} }^{1/2}\left[\mathbf {I} -\left(\mathbf {A} \mathbf {M} _{\mathbf {A} }^{-1/2}\right)^{+}\mathbf {A} \mathbf {M} _{\mathbf {A} }^{-1/2}\right]\mathbf {M} _{\mathbf {A} }^{-1/2}\mathbf {C} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab4276f77cda9a7912aea48ccce68dfc2246bee3)