Numero di Carmichael
|
Read other articles:

Holly WoodlawnWoodlawn pada 2007LahirHaroldo Santiago Franceschi Rodriguez Danhakl26 Oktober 1946Juana Díaz, Puerto RicoMeninggal6 Desember 2015 (usia 69)Los Angeles, California, ASSebab meninggalKanker otak dan kanker hatiNama lainHarold AjzenbergPekerjaanAktris Holly Woodlawn (26 Oktober 1946 – 6 Desember 2015) adalah seorang aktris dan superstar Warhol Puerto Rico transgender yang tampil dalam film-film Trash (1970) dan Women in Revolt (1972).[1][2&#...

Ashley RickardsLahirAshley Nicole Rickards4 Mei 1992 (umur 31)Sarasota, Florida, Amerika SerikatTahun aktif2006 — sekarang Ashley Nicole Rickards (lahir 4 Mei 1992) adalah seorang aktris berkebangsaan Amerika Serikat. Ia telah membintangi banyak film dan acara televisi salah satunya film Fly Away di mana ia memerankan tokoh Mandy. Namun ia mulai dikenal setelah berperan sebagai Jenna Hamilton dalam serial televisi remaja berjudul Awkward yang ditayangkan MTV. Kehidupan priba...

1995 video game 1995 video gameGalactic PinballDeveloper(s)Intelligent Systems[2]Publisher(s)NintendoDesigner(s)Kenji Yamamoto (Director)[3]Gunpei Yokoi (General Manager)[4][3]Composer(s)Kenji Yamamoto[3]Masaru Tajima[3]Platform(s)Virtual BoyReleaseJP: July 21, 1995NA: August 14, 1995[1]Genre(s)PinballMode(s)Single-player Galactic Pinball[a] is a pinball video game for Nintendo's Virtual Boy game console. The game was released on...

Ashoro 足寄町KotaprajaPemandangan Gunung Akan-Fuji yang dilihat dari Danau Onnetō. BenderaEmblemLokasi Ashoro di Hokkaido (Subprefektur Tokachi)AshoroLokasi di JepangKoordinat: 43°15′N 143°33′E / 43.250°N 143.550°E / 43.250; 143.550Koordinat: 43°15′N 143°33′E / 43.250°N 143.550°E / 43.250; 143.550NegaraJepangWilayahHokkaidoPrefektur Hokkaido (Subprefektur Tokachi)DistrikAshoroPemerintahan • WalikotaShun'ichi ...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (septembre 2014). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes. École nationale supérieure maritimeHistoireFon...

American lawyer For the filmmaker, see James C. McKay (director). Jim McKayPersonal detailsBorn(1917-02-24)February 24, 1917South Pasadena, California, U.S.DiedNovember 23, 2015(2015-11-23) (aged 98)Chevy Chase, Maryland, U.S.EducationCornell University (BA)Georgetown University (LLB) James C. Jim McKay (February 24, 1917 – November 23, 2015) was an American trial lawyer. As Independent Counsel from 1987 to 1990, he investigated allegations of illicit lobbying and conflicts of interest...

فلزات فلورية الفَلْوَرِيّة[1][2] أو التَّفَلْوُر[2][3][4] أو اللَّصَف[2][4] أو الإِسْتِشْعاع[4] (Fluorescence) تعرف بشكل عام بأنها إصدار ضيائي لمادة عندما يتوافق طول موجة الشعاع الساقط عليها مع مستويات الطاقة لذرات أو جزيئات تلك المادة. يحدث أن تثار تلك ...
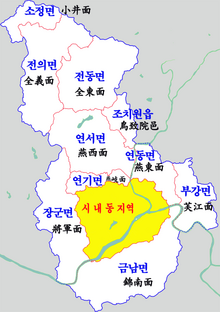
Sejong 세종Kota otonomi khususKota Otonomi Khusus SejongTranskripsi • Hangul세종특별자치시 • Hanja世宗特別自治市 • Alih Aksara BaruSejong Teukbyeol-jachisi • McCune-ReischauerSechong T’ŭkpyŏl-chach’isi Emblem Kota SejongPeta Korea Selatan dengan penyorotan SejongNegara Korea SelatanWilayahHoseoNeighbourhoodTownTownships119Pemerintahan • WalikotaLee Choon-heeLuas • Total465,23 km...

Maltese terrestrial television network Television channel Television Malta (TVM)CountryMaltaHeadquartersGwardamanġa, MaltaProgrammingLanguage(s)Maltese (main)English (secondary)Picture format1080i HDTVOwnershipOwnerPublic Broadcasting Services(Government of Malta)Sister channelsTVMNews+ TVMSport+ Parliament TVHistoryLaunched29 September 1962; 61 years ago (1962-09-29)Former namesMalta Television (MTV) (1962–1981)LinksWebsitetvmnews.mtAvailabilityTerrestrialFree-to-air43 (...

SMA Negeri 1 GarumInformasiNama latinSMANEGADidirikan25-01-1984AkreditasiANomor Pokok Sekolah Nasional20514351Kepala SekolahNur Cahyo Hadisunariyo S.PdJumlah kelasKelas X : 10 Kelas Kelas XI : 10 KelasKelas XII : 10 KelasJurusan atau peminatanIPA, IPSRentang kelasX IPA/IPS, XI IPA/IPS, XII IPA/IPSKurikulumKurikulum 2013Jumlah siswa>1000 siswaStatusNegeriAlamatLokasiJalan Raya Bence, Garum, Kabupaten Blitar, Jawa Timur, IndonesiaTel./Faks.(0342) 561395Sit...

Tributyl phosphate Spacefill model of Tributyl phosphate Ball and stick model of Tributyl phosphate Names Preferred IUPAC name Tributyl phosphate Identifiers CAS Number 126-73-8 Y 3D model (JSmol) Interactive image ChEBI CHEBI:35019 Y ChemSpider 29090 Y ECHA InfoCard 100.004.365 KEGG C14439 Y PubChem CID 31357 UNII 95UAS8YAF5 CompTox Dashboard (EPA) DTXSID3021986 InChI InChI=1S/C12H27O4P/c1-4-7-10-14-17(13,15-11-8-5-2)16-12-9-6-3/h4-12H2,1-3H3 YKey: STCOOQWBFONS...

Pour les articles homonymes, voir Alhazen (homonymie). Ne doit pas être confondu avec Albohazen ou Alassane. Alhazen Ibn al-Haytham Portrait d'Alhazen (extrait du frontispice de la Selenographia de l'astronome Hevelius publiée en 1647).Données clés Nom de naissance Abu Ali al-Hasan ibn al-Hasan ibn al-Haytham (ar) أبو علي، الحسن بن الحسن بن الهيثم Naissance c.965Bassora (Protectorat des Bouyides au sein du [Note 1] califat abbasside) Décès c.1040 (74-75 ans)L...

American politician (1823–1899) For other people with the same name, see John Harris (disambiguation). John Thomas HarrisMember of the U.S. House of Representativesfrom Virginia's 7th districtIn officeMarch 4, 1873 – March 3, 1881Preceded byElliott M. BraxtonSucceeded byJohn PaulChairman of the Committee on Revision of LawsIn officeMarch 4, 1879 – March 3, 1881Preceded byWilliam WalshSucceeded byWilliam C. OatesChairman of the Committee on ElectionsIn officeMarch 4, ...

Commercial building in Manhattan, New York Not to be confused with Manufacturers Hanover Trust Company Building (600 Fifth Avenue) in Rockefeller Center or with New York County National Bank Building (77–79 Eighth Avenue), originally designated as a New York City landmark under the name Manufacturers Hanover Trust Company Building. Manufacturers Trust Company BuildingFront of the building (2013)Former namesManufacturers Hanover Trust Company BuildingGeneral informationArchitectural styleInt...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

National forest in Montana and Idaho, United States Kootenai National ForestPanorama of the southern Cabinet MountainsLocationMontana-Idaho, United StatesNearest cityLibby, MTCoordinates48°11′N 115°28′W / 48.183°N 115.467°W / 48.183; -115.467Area2,200,000 acres (8,900 km2)Established1907Governing bodyU.S. Forest ServiceWebsiteKootenai National Forest The Kootenai National Forest is a national forest located in the far northwestern section of Mont...

This article's lead section may be too long. Please read the length guidelines and help move details into the article's body. (January 2022) COVID-19 pandemic in JapanConfirmed cases per 100,000 residents by prefecture[a]DiseaseCOVID-19Virus strainSARS-CoV-2LocationJapanFirst outbreakWuhan, Hubei, ChinaDate16 January 2020 - 21 April 2023(3 years, 3 months and 5 days)Confirmed cases33,803,572[1]Recovered33,728,878 (updated 23 July 2023) [2]Deaths74,694&#...

Public university in Magnolia, Arkansas, US Southern Arkansas UniversityFormer namesThird District Agricultural School (1909–1925)Agricultural and Mechanical College, Third District (1925–1951)Southern State College (1951–1976)TypePublic universityEstablished1909; 115 years ago (1909)Academic affiliationsSpace-grantEndowment$57 million[1]PresidentDavid F. Rankin (interim)ProvostDavid LanoueStudents5,128Undergraduates3,252Postgraduates1,876Doctoral students32Loc...

Map of the modern Falkland Islands Part of a series on the History of the Falkland Islands Colonial time French Empire Spanish Empire British Empire Continuous settlement Argentine settlement Reassertion of British sovereignty Battle of the Falkland Islands Argentine invasion Argentine occupation UNSCR 502 Falklands War Other Timeline Origins of Falkland Islanders vte The history of the Falkland Islands (Spanish: Islas Malvinas) goes back at least five hundred years, with active exploration ...

A Capitol Fourth35th anniversaryGenreMusic/performing artsOpening themeThe Star-Spangled Banner (except 1986)1812 Overture (1986 only)Ending theme1812 Overture (except 1986)The Star-Spangled Banner (1986 only)Country of originUnited StatesOriginal languageEnglishNo. of episodes41ProductionProduction locationsNational Mall, Washington, D.C. (1980–2019; 2022–present); broadcast but not live (2020–2021)Camera setupMulti-camera setupRunning time90 minutesOriginal releaseNetworkPBSReleaseJu...












