Numero armonico
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2017. Ri Han-jaeInformasi pribadiTanggal lahir 27 Juni 1982 (umur 41)Tempat lahir Prefektur Okayama, JepangPosisi bermain GelandangKarier senior*Tahun Tim Tampil (Gol)2001-2009 Sanfrecce Hiroshima 2010 Consadole Sapporo 2011-2013 FC Gifu 2014- FC Machida ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Balques Manisang – berita · surat kabar · buku · cendekiawan · JSTOR Balques ManisangLahirBalques Manisang11 November 1985 (umur 38)Manado, Sulawesi UtaraPekerjaanpembaca berita, presenter, moderato...

The TimesHalaman depannya dari edisi 17 Oktober 2007TipeHarian surat kabarFormatCompactPemilikTimes Newspapers LtdRedaksiJames HardingDidirikan1785Pandangan politikCentre-rightPusatWapping, LondonSirkulasi surat kabar618,160 [1]Situs webwww.timesonline.co.uk The Times adalah surat kabar harian yang diterbitkan di Inggris Raya sejak tahun 1785, ketika itu masih dikenal dengan nama The Daily Universal Register. Surat kabar ini dan saudaranya The Sunday Times diterbitkan oleh Times Newsp...

Benzodiazepine medication ClorazepateClinical dataTrade namesTranxene, Tranxilium, Novo-ClopateOther namesClorazepate dipotassiumAHFS/Drugs.comMonographMedlinePlusa682052Routes ofadministrationOralATC codeN05BA05 (WHO) Legal statusLegal status BR: Class B1 (Psychoactive drugs)[1] CA: Schedule IV DE: Prescription only (Anlage III for higher doses) UK: Class C US: Schedule IV Pharmacokinetic dataBioavailability91%MetabolismHepaticElimination half-life4...

American politician (1908–1992) Quentin BurdickOfficial portrait of Burdick c. 1975United States Senatorfrom North DakotaIn officeAugust 8, 1960 – September 8, 1992Preceded byNorman BrunsdaleSucceeded byJocelyn BurdickMember of the U.S. House of Representativesfrom North Dakota's At-large districtIn officeJanuary 3, 1959 – August 8, 1960Preceded byUsher L. BurdickSucceeded byHjalmar Nygaard Personal detailsBornQuentin Northrup Burdick(1908-06-19)June ...

PausLusius IIAwal masa kepausan9 Maret 1144Akhir masa kepausan15 Februari 1145PendahuluSelestinus IIPenerusEugenius IIIInformasi pribadiNama lahirGherardo Caccianemici dal OrsoLahir???Bologna, ItaliaWafat15 Februari 1145Roma, Italia Lusius II, nama lahir Gherardo Caccianemici dal Orso (wafat di Roma, Italia, 15 Februari 1145), adalah Paus Gereja Katolik Roma sejak 9 Maret 1144[1] sampai 15 Februari 1145. Referensi ^ Salinan arsip. Diarsipkan dari versi asli tanggal 2011-03-14. Diakses...

Украинская пропагандистская листовка, 1917 год Пропаганда в Украинской Народной Республике (УНР) представляла собой важный аспект государственной деятельности в период её существования в начале XX века. УНР боролась за свою независимость, и пропаганда использовалас...

American government-owned company This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (October 2018) (Learn how and whe...

Kolkata Municipal Corporation in West Bengal, IndiaWard No. 60Kolkata Municipal CorporationInteractive Map Outlining Ward No. 60Ward No. 60Location in KolkataCoordinates (dms): 22°32′50″N 88°22′10″E / 22.547333°N 88.369325°E / 22.547333; 88.369325Country IndiaStateWest BengalCityKolkataNeighbourhoodsPark Circus, BeniapukurReservationOpenParliamentary constituencyKolkata DakshinAssembly constituencyBallygungeBorough6Population (2011) •&...

Buswillercomune Buswiller – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Basso Reno ArrondissementSaverne CantoneBouxwiller TerritorioCoordinate48°49′N 7°34′E / 48.816667°N 7.566667°E48.816667; 7.566667 (Buswiller)Coordinate: 48°49′N 7°34′E / 48.816667°N 7.566667°E48.816667; 7.566667 (Buswiller) Altitudine199-275 m s.l.m. Superficie2,3 km² Abitanti193[1] (2009) Densità83,91 ab./km² Al...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

Town in Devon, England Not to be confused with Oakhampton in New South Wales, Australia. Human settlement in EnglandOkehamptonBaptist Chapel, Fore Street, built 1889OkehamptonLocation within DevonPopulation5,922 (2011)OS grid referenceSX5895• London201 miles (323 km)Civil parishOkehamptonDistrictWest DevonShire countyDevonRegionSouth WestCountryEnglandSovereign stateUnited KingdomPost townOKEHAMPTONPostcode districtEX20Dialling code01837PoliceDev...

2021 American short documentary film How Do You Measure a Year?Official posterDirected byJay RosenblattProduced byJay RosenblattStarring Ella Rosenblatt CinematographyThomas LogoreciJay RosenblattEdited byJay RosenblattDistributed bySubmarineRelease date 13 August 2021 (2021-08-13) (Locarno) Running time29 minutesCountry United States LanguageEnglish How Do You Measure a Year? is a 2021 American short documentary film directed by Jay Rosenblatt. The documentary film is abou...

List of definitions of terms and concepts commonly used in the study of physics This glossary of physics is a list of definitions of terms and concepts relevant to physics, its sub-disciplines, and related fields, including mechanics, materials science, nuclear physics, particle physics, and thermodynamics. For more inclusive glossaries concerning related fields of science and technology, see Glossary of chemistry terms, Glossary of astronomy, Glossary of areas of mathematics, and Glossary of...

National holiday of Spain (October 12) This article is written like a travel guide. Please help improve the article by introducing an encyclopedic style or move the content to Wikivoyage. (October 2022) National Day of SpainOfficial nameFiesta Nacional de EspañaObserved bySpainDate12 OctoberNext time12 October 2024 (2024-10-12)FrequencyAnnual The coat of arms of Spain displays the symbols of both medieval and modern Spain and the key transition event between them, the discover...

كمال الملاخ كمال وليم يونان الملاخ معلومات شخصية الميلاد 26 أكتوبر 1918(1918-10-26)أسيوط، مصر الوفاة 29 أكتوبر 1987 (69 سنة)القاهرة، مصر الجنسية مصري الديانة مسيحي الحياة العملية المدرسة الأم جامعة القاهرة المهنة كاتب وصحفي وعالم مصريات اللغة الأم العربية اللغات العربي�...

Pandemi COVID-19 di Slowakia 0-99 kasus 100-149 kasus 150-199 kasus 200-249 kasus 250-299 kasus 300-349 kasus 350-399 kasusPenyakitCOVID-19Galur virusSARS-CoV-2LokasiSlovakiaKasus pertamaKostolišteTanggal kemunculan6 March 2020(4 tahun, 3 bulan, 1 minggu dan 6 hari ago)AsalWuhan, TiongkokKasus terkonfirmasi1,893Kasus dirawat372Kasus sembuh1,493Kematian28Situs web resmikorona.gov.sk Pandemi COVID-...

Questa voce è orfana, ovvero priva di collegamenti in entrata da altre voci. Inseriscine almeno uno pertinente e utile e rimuovi l'avviso. Segui i suggerimenti del progetto di riferimento. Una Lucy Fielding Una Lucy Fielding (Wellington, 20 maggio 1888 – Londra, 11 agosto 1969) è stata un'anatomista e neurologa australiana. Biografia Maggiore di sei figli, Una Fielding nacque a Wellington, nel Nuovo Galles del Sud, e frequentò una scuola privata a Windsor prima di iniziare a studiare al...

AuthorRicky JayGenreTheatrePublisherVillard Books; Farrar, Straus and GirouxPublication date1986, 1998Pages343ISBN978-0-374-52570-5Dewey Decimal790.20922, 791.0922 Learned Pigs & Fireproof Women is a book written by stage magician, actor and writer Ricky Jay.[1] Divided into numerous themed chapters, the book provides the bizarre histories of some of the world's most eccentric entertainers, ranging from mind readers and daredevils to animal handlers and stone eaters. Jay presents...

Association football club in England Football clubAlfoldFull nameAlfold Football ClubNickname(s)The FoldFounded1920GroundThe Recreation Ground, AlfoldChairmanTerry EamesManagerSimon FunnellLeagueSouthern Combination Division One2023–24Southern Combination Division One, 15th of 18 Home colours Away colours Alfold Football Club is a football club based in Alfold, Surrey, England. They are currently members of the Southern Combination Division One and play at the Recreation Ground. History The...
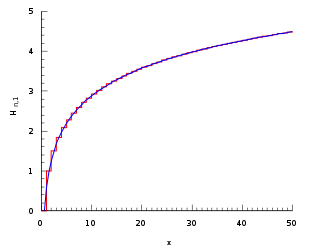


![{\displaystyle \gamma +\ln[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a16fb50fd16271d045dcb8cb474494fe53c9ca26)






