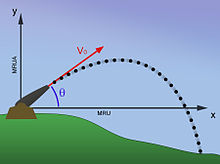
Moto (fisica)

Stazione ferroviaria di Yongsan

In fisica il moto è il cambiamento di posizione di un corpo in funzione del tempo, misurato da uno specifico osservatore in un determinato sistema di riferimento. Fino al XIX secolo, le leggi di Newton, incluse tra gli assiomi e i postulati del famoso Philosophiae Naturalis Principia Mathematica, erano alla base di quella parte della meccanica classica nota come "cinematica". Lo studio del moto a partire dalle cause che lo generano ovvero le forze è noto invece come "dinamica".

Esempio di traiettoria balistica

Storicamente il problema del moto è stato dunque il primo problema affrontato dalla fisica, direttamente applicato al moto dei corpi celesti con la meccanica celeste nell'ambito della rivoluzione scientifica. I calcoli delle traiettorie e delle forze esercitate dai corpi in moto basati sulle leggi newtoniane e delle fisica classica, si dimostrarono efficaci fintanto che i fisici non si occuparono di fenomeni molto rapidi, come quelli della fisica atomica agli inizi del XX secolo.

La forza del moto si chiama "forza d'inerzia".

Tipologie di moto

Moto circolare
Moto elicoidale uniforme

Esistono vari tipi di moto in base alla forma del percorso seguito da un corpo durante il suo moto nello spazio, ad esempio: rettilineo, curvilineo, circolare, parabolico ed ellittico. Tali forme sono dette "traiettorie".

Tra i moti della fisica classica, si ricordano:

Tra i moti della fisica atomica e subatomica e dell'astrofisica, si ricordano:

Principio di indipendenza dei moti simultanei

Nello studio del moto di un corpo particolarmente utile risulta il cosiddetto "Principio di indipendenza dei moti simultanei" il quale afferma che "il moto di un corpo lungo una certa traiettoria nello spazio è la risultante ovvero la composizione di singoli moti ciascuno lungo le direzioni degli assi cartesiani nello spazio"[1].

Grazie all'applicazione di tale principio, le traiettorie più complesse (ad esempio: traiettorie tridimensionali) possono essere descritte come composizione di singoli moti.

Note

  1. ^ Altri enunciati equivalenti, risalenti a Galileo Galilei, "Se un corpo è animato contemporaneamente da due movimenti, ciascuno dei due continua ad essere caratterizzato dalle stesse leggi che lo regolano quando si svolge da solo" oppure "Un corpo soggetto a due movimenti simultanei dopo un tempo t occupa la stessa posizione che occuperebbe se avesse eseguito i due movimenti successivamente uno dopo l'altro" possono essere letti in http://www.massimobanfi.it/Sito/fisicamatematica/appunti/Cap.%206%20-%20La%20cinematica%20dei%20moti%20piani.pdf

Voci correlate

Altri progetti

Collegamenti esterni

Controllo di autoritàThesaurus BNCF 9475 · LCCN (EN) sh85087557 · BNF (FR) cb119798925 (data) · J9U (EN, HE) 987007545931005171
  Portale Fisica: accedi alle voci di Wikipedia che trattano di fisica

Read other articles:

羅生門 (電影)

本條目存在以下問題，請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目，无法查证的内容可能會因為异议提出而被移除。致使用者：请搜索一下条目的标题（来源搜索：羅生門 (電影) — 网页、新闻、书籍、学术、图像），以检查网络上是否存在该主题的更多可靠来源（判定指引）。 �...

 

Philadelphia Flyers

National Hockey League team in Philadelphia, Pennsylvania The Flyers redirects here. For other uses, see Flyer. Broad Street Bullies redirects here. For the documentary, see Broad Street Bullies (film). For other uses, see Broadstreet bully. Philadelphia Flyers 2023–24 Philadelphia Flyers seasonConferenceEasternDivisionMetropolitanFounded1967HistoryPhiladelphia Flyers1967–presentHome arenaWells Fargo CenterCityPhiladelphia, PennsylvaniaTeam colorsBurnt orange, black, white[1][...

 

Partenariat oriental

Partenariat oriental Description Volet de la politique européenne de voisinage Création 7 mai 2009(14 ans, 10 mois et 23 jours) Membres Arménie Azerbaïdjan Géorgie Moldavie Ukraine Union européenne Compléments Site internet Service européen pour l'action extérieure modifier  Le partenariat oriental est une politique de voisinage de l'Union européenne visant à conclure des accords avec l'Arménie, l'Azerbaïdjan, la Géorgie, la Moldavie, l'Ukraine et la Bi...

Pecos Bill

Fictional cowboy This article is about the fictional character. For the restaurant, see Pecos Bill Tall Tale Inn and Cafe. For other uses, see Pecos Bill (disambiguation). Fictional character Pecos BillOn one of his various adventures, Bill managed to lasso a tornado using a snakeFirst appearanceSaga of Pecos Bill (1917)Created byEdward S. O'ReillyBirthplaceTexasIn-universe informationFull namePecos BillSpeciesHumanGenderMaleOccupationCowboySignificant otherSlue-Foot SueNationalityAmerican Pe...

 

Aircraft principal axes

Principal directions in aviation This article is about yaw, pitch, and roll as symmetry axes of an aircraft. For meaning in mechanics, see Moment of inertia § Principal axes. For Euler angles with the same names, see Euler angles § Tait–Bryan angles. The position of all three axes, with the right-hand rule for describing the angle of its rotations An aircraft in flight is free to rotate in three dimensions: yaw, nose left or right about an axis running up and down; pitch, nose u...

 

Der Herr der Ringe Online

Der Herr der Ringe Online Originaltitel The Lord of the Rings Online Entwickler Turbine Inc.,Standing Stone Games Publisher Daybreak Game Company Komponist Chance Thomas,Stephen DiGregorio,Bill Champagne,Matthew Harwood Veröffentlichung 24. April 2007 Plattform Windows, macOS Genre Massively Multiplayer Online Role-Playing Game Thematik Fantasy Spielmodus Mehrspieler Sprache u. a. Deutsch und Englisch Aktuelle Version 38.1 Altersfreigabe USK USK ab 12 freigegeben PEGI PEGI ab 12 Ja...

普密蓬·阿杜德

普密蓬·阿杜德ภูมิพลอดุลยเดช泰国先王普密蓬·阿杜德（官方肖像） 泰國國王統治1946年6月9日－2016年10月13日（70年126天）加冕1950年5月5日前任阿南塔玛希敦繼任玛哈·哇集拉隆功总理见列表出生(1927-12-05)1927年12月5日 美國马萨诸塞州剑桥奥本山醫院（英语：Mount Auburn Hospital）逝世2016年10月13日(2016歲—10—13)（88歲） 泰國曼谷西里拉醫院安葬曼谷僧...

 

W. Kamau Bell

American comedian and television host (born 1973) W. Kamau BellBell in 2018Birth nameWalter Kamau BellBorn (1973-01-26) January 26, 1973 (age 51)Palo Alto, California, U.S.MediumStand-up comedyNationalityAmericanEducationUniversity of Chicago Laboratory SchoolsAlma materUniversity of Pennsylvania (dropped out)Years active2005–presentSubject(s)Racism, social identity, inequality, American politicsSpouse Melissa Hudson Bell ​(m. 2009)​Children3Paren...

 

中华人民共和国国家元首列表

  提示：此条目页的主题不是中華人民共和國最高領導人。 中华人民共和国 中华人民共和国政府与政治系列条目 执政党 中国共产党 党章、党旗党徽 主要负责人、领导核心 领导集体、民主集中制 意识形态、组织 以习近平同志为核心的党中央 两个维护、两个确立 全国代表大会 （二十大） 中央委员会 （二十届） 总书记：习近平 中央政治局 常务委员会 中央书记处 �...

土库曼斯坦总统

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府（Oguzkhan Presidential Palace）機關所在地阿什哈巴德任命者直接选举任期7年，可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關（英语：National Council of Turkmenistan） ...

 

British Overseas Territories citizen

Type of British nationality Not to be confused with British Overseas citizen. British citizenship andnationality law Introduction British nationality law (History) Nationality classes British citizens British subjects(under the British Nationality Act 1981) British Overseas Territories citizens British Nationals (Overseas) British Overseas citizens British protected persons See also Commonwealth citizens British passports Right of abode Indefinite leave to remain Belonger status(in certain Br...

 

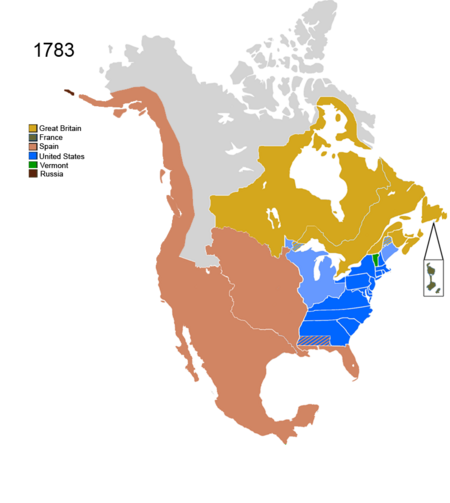
History of United States foreign policy

Aspect of US history Further information: Foreign policy of the United States and Timeline of United States diplomatic history This article is part of a series on theHistory of the United States Timeline and periodsPrehistoric and Pre-Columbian Erauntil 1607Colonial Era 1607–17651776–1789    American Revolution 1765–1783    Confederation Period 1783–17881789–1815    Federalist Era 1788–1801    Jefferso...

Système décimal

Ne doit pas être confondu avec Nombre décimal. Le système décimal est un système de numération utilisant la base dix. Dans ce système, les puissances de dix et leurs multiples bénéficient d'une représentation privilégiée. Numérations décimales Le système décimal est largement le plus répandu. Ainsi sont constituées, par exemple, les numérations : indo-arabe (dont nos chiffres arabes), arménienne, chinoise, égyptienne, gotique, grecque, hébraïque, indienne, japonai...

 

جوتشي

جزء من سلسلة مقالات سياسة كوريا الشماليةكوريا الشمالية الدستور الدستور الزوتشية الرئيس الأبدي للجمهورية كم إل سونغ حقوق الإنسان السلطة التنفيذية الرئيس مجلس الوزراء السلطة التشريعية الجمعية الشعبية العليا السلطة القضائية القضاء الانتخابات الانتخابات الأحزاب السياسية...

 

Emma Stone

American actress and producer (born 1988) Emma StoneStone at the 2024 Cannes Film FestivalBornEmily Jean Stone (1988-11-06) November 6, 1988 (age 35)Scottsdale, Arizona, U.S.OccupationsActressproducerYears active2004–presentOrganizationFruit TreeWorksFull listSpouse Dave McCary ​(m. 2020)​Children1AwardsFull listSignature Emily Jean Emma Stone (born November 6, 1988) is an American actress and producer. Her works include blockbusters and independent fi...

كلية الموسي للعلوم الصحية

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2020) كلية الموسي للعلوم الصحية شعار كلية الموسي للعلوم الصحية معلومات التأسيس 2019 (منذ 5 سنوات) النوع كلية الموقع الجغرافي المدينة الأحساء البلد السعودية إحصاءات...

 

قائمة معتقلي غوانتانامو

معتقلون يلبسون الزي البرتقالي عند وصولهم إلى القاعدة العسكرية في يناير 2002 اعتقلت الولايات المتحدة الأمريكية أكثر من 779 معتقلاً إدارياً خارج نطاق القضاء في معتقل غوانتانامو الأمريكي في كوبا منذ فتح معسكرات الاعتقال في 11 يناير 2002، وانخفض العدد إلى 160 تقريبًا في ديسمبر 2013.[...

 

The Lost World (TV series)

American action/adventure television series Not to be confused with Lost Worlds (TV series). The Lost WorldSeason one titlecardGenreActionAdventureScience fantasyBased onThe Lost Worldby Arthur Conan DoyleStarring Peter McCauley Rachel Blakely William Snow David Orth Jennifer O'Dell Michael Sinelnikoff Country of origin Canada Australia United States Original languageEnglishNo. of seasons3No. of episodes66 (list of episodes)ProductionExecutive producers Greg Coote Jeffery Hayes Guy Mullally J...

Turkmenistan women's national football team

Turkmenistan women's national association football team This article is about the women's team. For the men's team, see Turkmenistan national football team. TurkmenistanAssociationFootball Federation of Turkmenistan(Türkmenistanyň Futbol federasiýasy)ConfederationAFC (Asia)Sub-confederationCAFA (Central Asia)Head coachKamil Mingazow[1]CaptainMariýa ÇaryýewaTop scorerSwetlana Prýannikowa (1)FIFA codeTKM First colours Second colours FIFA rankingCurrent 139 (14 June 2024)[2 ...

 

Giovanni Bernardi

Italian sculptor The Punishment of Tityos, rock crystal intaglio by Giovanni Bernardi, the British Museum Giovanni Bernardi (1494 – 22 May 1553), also known as Giovanni da Castel Bolognese and as Giovanni da Castelbolognese, was an Italian gem engraver and medallist who was born in Castel Bolognese, Italy. He was the son of a goldsmith and by 1530 had moved to Rome, where he had a position in the Papal mint, which also allowed him time to work for other patrons. These included Cardinal ...