Lossodromia
|
Read other articles:
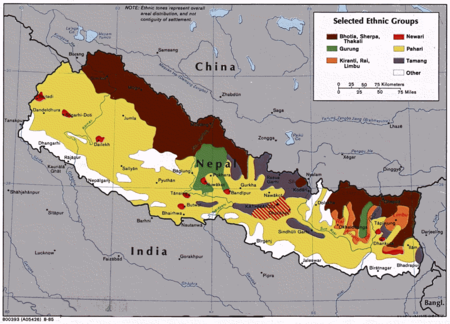
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of Nepali musical instruments – news · newspapers · books · scholar · JSTOR (November 2020) (Learn how and when to remove this template message) Newar merchants of Kathmandu, Nepal parading in Lhasa, Tibet playing drums in 1903. This list contains traditi...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 �...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Енотовидная собака Енотовидная собака в гродненском зоопарке (Беларусь) Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкл�...

Protected area in Lanaudière, Quebec, Canada Kiamika Reservoir Regional ParkLocationCanada, Quebec, Laurentides, Antoine-Labelle Regional County MunicipalityNearest townLac-DouaireCoordinates46°40′22″N 75°05′24″W / 46.67278°N 75.09°W / 46.67278; -75.09Area184 square kilometres (71 sq mi)reservoirkiamika.org The Kiamika Reservoir Regional Park (in French: Parc régional du Réservoir-Kamika) is a regional park located in the unorganized terri...

Шалфей обыкновенный Научная классификация Домен:ЭукариотыЦарство:РастенияКлада:Цветковые растенияКлада:ЭвдикотыКлада:СуперастеридыКлада:АстеридыКлада:ЛамиидыПорядок:ЯсноткоцветныеСемейство:ЯснотковыеРод:ШалфейВид:Шалфей обыкновенный Международное научное наз...

Variety of grape This article is about the grape. For the river in Iceland, see Glerá. For another type of grape called Glera, see Ribolla Gialla. GleraGrape (Vitis)Prosecco sparkling wine made from GleraColor of berry skinBlancSpeciesVitis viniferaAlso calledProsecco and other synonymsOriginItalyNotable regionsVenetoNotable winesProseccoVIVC number9741 Glera is a white variety of grape of Italian origin, possibly from the namesake village, Prosecco. The variety was formerly mostly referred ...

Former railway station in Warwickshire, England Studley & Astwood BankThe site of the station in 2014General informationLocationStudley, WarwickshireEnglandCoordinates52°16′16″N 1°54′50″W / 52.2711°N 1.9140°W / 52.2711; -1.9140Grid referenceSP059636Platforms1Other informationStatusDisusedHistoryOriginal companyEvesham and Redditch RailwayPre-groupingMidland RailwayPost-groupingLondon, Midland and Scottish RailwayKey dates4 May 1868Opened[1]1 Oct...
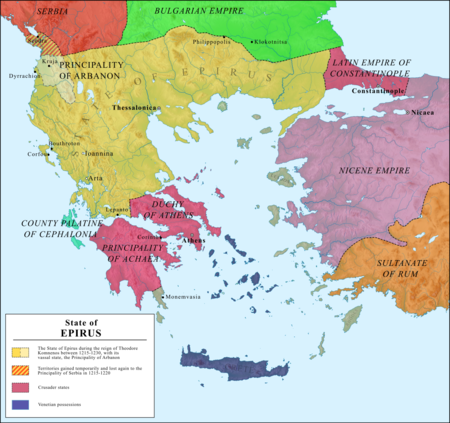
Medieval Albanian state Principality of ArbanonPrincipata e Arbërit (Albanian)1190–1215/16[1][2][3] (annexed ca. 1256/57)[4]Arbanon/Arbëria, ca. 1208StatusPrincipality[5][6]CapitalKrujëCommon languagesAlbanianReligion Roman CatholicismEastern Orthodoxy[7]Prince • 1190–1198 Progon (first)• 1198–1208 Gjin Progoni• 1208–1216 Dhimitër Progoni• 1216–1236 Grigor Kamona• 1252–125...

National gemstone of Ireland The distinct green colour of the middle slab is a result of an abundance of serpentine minerals Connemara marble ornament, Museum Building, Trinity College Dublin Connemara marble or Irish green is a rare variety of green marble from Connemara, Ireland. It is used as a decoration and building material.[1][2] Its colour causes it to often be associated with the Irish identity, and for this reason it has been named the national gemstone of Ireland. I...

銮披汶·頌堪แปลก พิบูลสงคราม第3任泰國總理任期1938年12月16日—1944年8月1日君主國王拉玛八世前任披耶帕凤侯爵继任寬·阿派旺第8任泰國總理任期1948年4月8日—1957年9月16日君主國王拉玛九世前任寬·阿派旺继任乃朴·沙拉信 个人资料出生貝·基達桑卡(1897-07-14)1897年7月14日 暹罗暖武里府逝世1964年6月11日(1964歲—06—11)(66歲) 日本神奈川縣相模原市国籍&#...

20th Century Limited20th Century Limited yang efisien berangkat dari Chicago untuk uji coba pada bulan Juni 1938Informasi umumStatusDihentikanMulai beroperasi17 Juni 1902Terakhir beroperasi2 Desember 1967PenerusLake Shore LimitedOperator sebelumnyaNew York Central RailroadLintas pelayananStasiun awalNew YorkStasiun akhirChicagoFrekuensi perjalananHarianPeta ruteTemplat:20th Century Limited 20th Century Limited adalah kereta penumpang ekspres di New York Central Railroad (NYC) dari tahun 1902 ...

دوري كرة القدم الإسكتلندي الدرجة الأولى 1982–83 تفاصيل الموسم دوري كرة القدم الإسكتلندي الدرجة الأولى [لغات أخرى] البلد المملكة المتحدة البطل سانت جونستون مباريات ملعوبة 273 عدد المشاركين 14 دوري كرة القدم الإسكتلندي الدرجة الأولى 1981–82 دوري كرة...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Philosophical and theological term For the belief in being able to contact the dead, see Spiritualism (beliefs). Part of a series onSpirituality Outline Religion History Timeline Traditional Elite religion Jewish Merkabah Kabbalah Hasidism Christian Catholic Mysticism Sufism Folk religion Modern Buddhist modernism New religious movement Secular spirituality Spiritual but not religious Syncretism Spiritual experience Lived religion Mystical experience Oceanic feeling Religious experience Relig...

Overview of the agriculture in Italy Vineyards in Langhe and Montferrat, Piedmont. Italy is the world's largest wine producer (22% of global market), as well as the country with the widest variety of indigenous grapevine in the world.[1][2][3]. Agriculture in Italy, one of the economic sectors of the country, has developed since the 5th millennium BC. In the 20th century, Italy transformed from a predominantly agricultural country to an industrial country. As a result,...

Indian Kannada-language newspaper This article may need to be rewritten to comply with Wikipedia's quality standards. You can help. The talk page may contain suggestions. (September 2016) Karavali AleFront page of the Mangalore edition of Karavali Ale, dated March 9, 2022.TypeDaily newspaperFormatBroadsheetOwner(s)B. V. Seetaram, Rohini S.PublisherChitra Publications Pvt. Ltd.Editor-in-chiefB. V. SeetaramFounded2 December 1992; 31 years ago (1992-12-02)LanguageKannadaHeadqua...

تقليح الأسنان وكشط الجذر Scaling and root planing صورة عن قرب لمقلحة الأسنان اليدوية تعديل مصدري - تعديل تَقليح الأسنان وكَشط الجذر، أو كما تعرف بالطريقة الاعتيادية أو غير الجراحية لعلاج الأنسجة الداعمة للأسنان، أو التنظيف العميق للأسنان. هي عبارة عن عملية إزالة العوامل المسبِّ...

See also: Scuba skills and Surface-supplied diving skills Standardised methods of doing things that are known to work effectively and acceptably safely Diving procedures are standardised methods of doing things that are commonly useful while diving that are known to work effectively and acceptably safely. Due to the inherent risks of the environment and the necessity to operate the equipment correctly, both under normal conditions and during incidents where failure to respond appropriately an...

0°29′03″S 117°08′41″E / 0.48429°S 117.14485°E / -0.48429; 117.14485 Politeknik Kesehatan Kementerian Kesehatan Kalimantan TimurGerbang menuju PoltekkesDidirikan16 April 2001 Politeknik Kesehatan Kementerian Kesehatan Kalimantan Timur (disingkat: Poltekkes Kemenkes Kalimantan Timur) adalah sebuah perguruan tinggi berbasis politeknik yang berlokasi di Jalan Wolter Monginsidi, Kota Samarinda, Kalimantan Timur, Indonesia. Sejarah Politeknik Kesehatan (Poltekkes...


















