Ipertetraedro
| |||||||||||||||||||||||||
Read other articles:

Revolusi OktoberBagian dari Revolusi Rusia dan Revolusi 1917–23Istana Musim Dingin di Petrograd sehari setelah pemberontakan, 8 NovemberTanggal7 November 1917 (K.J. 25 Oktober 1917)LokasiPetrograd, Republik RusiaHasil Kemenangan Bolshevik Berakhirnya sistem kekuasaan ganda Pembubaran Republik Rusia Kongres Soviet Kedua memproklamirkan dirinya sebagai badan pemerintahan tertinggi di negara ini Kerensky dan Krasnov gagal merebut kembali ibu kota Pemilihan Majelis Konstituen Rusia diadakan di ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Edgar dari Inggris – berita · surat kabar · buku · cendekiawan · JSTOR EdgarRaja InggrisBerkuasa1 Oktober 959 – 8 Juli 975PendahuluEadwigPenerusEdwardInformasi pribadiKelahiran(943-08-07)7 Agustus 943W...

Negeri Sembilan FCJulukanSi Rusa The JangsBerdiri1923StadionStadion Tuanku Abdul Rahman, Negeri Sembilan(Kapasitas: 40.000[1])PemilikNegeri Sembilan Football ClubKetuaMohammad HassanPelatihGary Michael PhillipsLigaLiga Utama Malaysia2019Ke-6Situs webSitus web resmi klub Kostum kandang Kostum tandang Negeri Sembilan FC adalah klub sepak bola yang berlaga di Liga Utama Malaysia. Klub ini bermarkas di Seremban, Negeri Sembilan. Klub ini berganti nama menjadi NS Matrix FC saat dimula...

Pembentukan bintang adalah proses di mana daerah padat di dalam awan molekul di ruang antarbintang, kadang-kadang disebut sebagai pembuahan bintang atau daerah pembentuk bintang, runtuh dan membentuk bintang.[1] Sebagai cabang astronomi, pembentukan bintang mencakup studi tentang medium antarbintang dan awan molekul raksasa sebagai prekursor proses pembentukan bintang, dan studi tentang protobintang dan objek bintang muda sebagai produk langsungnya. Ini terkait erat dengan pembentukan...

2008 2020 Élections sénatoriales de 2014 dans les Alpes-de-Haute-Provence 28 septembre 2014 Type d’élection Élections sénatoriales Postes à élire 1 siège de sénateur Jean-Yves Roux – PS Voix au 1er tour 127 23,61 % Voix au 2e tour 214 41,23 % Bernard Jeanmet-Peralta – UMP Voix au 1er tour 137 25,46 % Voix au 2e tour 162 31,21 % Jacques Depieds – DVD Voix au 1er tour 114 21,19 % Voix au 2e to...

The Pirate Bay Adresse thepiratebay.orgPar réseau Tor : adresse .onion[1] Description plateforme de recherche Torrents Slogan « The galaxy's most resilient BitTorrent site » Commercial Non Publicité Oui Langue 35 langues différentes Inscription Facultatif Propriétaire Gottfrid Svartholm, Fredrik Neij, Peter Sunde Créé par Gottfrid Svartholm, Fredrik Neij, Peter Sunde, Alex Martins Lancement 15 septembre 2003 Revenus les dons et la publicité État actuel ...

Bandar MasilamKecamatanPeta lokasi Kecamatan Bandar MasilamNegara IndonesiaProvinsiSumatera UtaraKabupatenSimalungunPemerintahan • Camat-Populasi • Total- jiwaKode Kemendagri12.08.24 Kode BPS1209191 Luas- km²Desa/kelurahan10 desa Bandar Masilam adalah sebuah kecamatan di Kabupaten Simalungun, Sumatera Utara, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Administras...
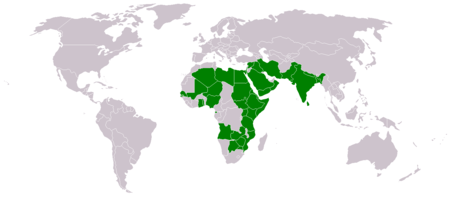
اضغط هنا للاطلاع على كيفية قراءة التصنيف السنط العربي رسم توضيحي لنبات السنط النيلي حالة الحفظ أنواع غير مهددة أو خطر انقراض ضعيف جدا [1] المرتبة التصنيفية نوع التصنيف العلمي النطاق: حقيقيات النوى المملكة: النباتات الشعبة: البذريات الشعيبة: مستورات البذور الرتب...

BicazKotaLetak BicazNegara RumaniaCountyCounty NeamţStatusKotaPemerintahan • Wali kotaNicolae Sălăgean (Partidul Social Democrat)Luas • Total148,9 km2 (575 sq mi)Populasi (2002) • Total8.643Zona waktuUTC+2 (EET) • Musim panas (DST)UTC+3 (EEST) Bicaz adalah sebuah kota yang terletak di County Neamţ, Rumania. Kota ini terletak di sebelah timur Pegunungan Carpathia, di dekat pertemuan antara sungai Bicaz dan Bistriţa. ...

Footballer (born 1994) Mohamed Elyounoussi Elyounoussi with Basel in 2017Personal informationFull name Mohamed Amine Elyounoussi[1]Date of birth (1994-08-04) 4 August 1994 (age 29)[2]Place of birth Al Hoceima, MoroccoHeight 1.78 m (5 ft 10 in)[3]Position(s) Forward, wingerTeam informationCurrent team CopenhagenNumber 10Youth career Sarpsborg FK Sarpsborg 08Senior career*Years Team Apps (Gls)2011–2014 Sarpsborg 08 64 (15)2014–2016 Molde 70 (30)20...

Douglas B-66 Destroyer adalah pesawat bomber ringan pengintai (reconnaissance aircraft) Angkatan Udara Taktis Komando Udara AS berdasarkan A-3 Skywarrior Angkatan Laut Amerika Serikat. Hal itu dimaksudkan untuk menggantikan Douglas A-26 Invader. BPR-66 versi foto-pengintai dipesan secara bersamaan. B-66 USAF mempertahankan awak tiga orang dari USN A-3, tetapi juga dimasukkan kursi ejeksi. Referensi Baugher, Joe. Douglas B-66 Destroyer. USAAC/USAAF/USAF Bomber Aircraft: Third Series of USAAC/...

这是马来族人名,“莫哈末·雅辛”是父名,不是姓氏,提及此人时应以其自身的名“慕尤丁”为主。 尊敬的丹斯里拿督哈芝慕尤丁·莫哈末雅辛馬來語:Muhyiddin Mohd YassinMahiaddin bin Md Yasin(注册名)国会议员PSM; SPMJ; SHMS; SPSA; SPMP; SUNS; SPDK; DP; PNBS; SMJ; BSI (I); PIS (I)2021年的慕尤丁 第8任马来西亚首相任期2020年3月1日—2021年8月20日君主國家元首蘇丹阿都拉副职依斯迈沙比里前任马...

Seven Springs of ApinkAlbum mini karya ApinkDirilis19 April 2011 (2011-04-19)DirekamCube Studio, Seoul, Korea Selatan2011GenreK-pop, dance-popDurasi15:30LabelA Cube EntertainmentCJ E&M Music and LiveKronologi Apink Seven Springs of Apink(2011) Snow Pink(2011)Snow Pink2011 Singel dalam album Seven Springs of Apink I Don't KnowDirilis: 19 April 2011 WishlistDirilis: 20 Mei 2011 It GirlDirilis: 23 Juni 2011 Seven Springs of Apink adalah album mini debut grup vokal wanita Korea Selat...

سفارة أوكرانيا في قبرص أوكرانيا قبرص الإحداثيات 35°09′21″N 33°18′53″E / 35.155958°N 33.314648°E / 35.155958; 33.314648 البلد قبرص المكان نيقوسيا الاختصاص قبرص الموقع الالكتروني الموقع الرسمي تعديل مصدري - تعديل سفارة أوكرانيا في قبرص هي أرفع تمثيل دبلوماسي[1] لدولة أوك...

православна єпархіяd Шепетівська єпархія Герб єпархії Основні даніЦерква Українська православна церква (Московський патріархат)Заснована 2007Юрисдикція Хмельницька областьЄпархіальний центр ШепетівкаКафедральний собор Saint Michael Archangel Orthodox Cathedral in ShepetivkadБлагочинь 6Пара�...

Not to be confused with Queen Alexandra Range. Mountain range in Antarctica Alexandra Mountains GeographyRange coordinates77°25′S 153°30′W / 77.417°S 153.500°W / -77.417; -153.500 (Alexandra Mountains) The Alexandra Mountains (77°25′S 153°30′W / 77.417°S 153.500°W / -77.417; -153.500 (Alexandra Mountains)) are a group of low, separated mountains in the north portion of Edward VII Peninsula, just southwest of Sulzb...

盐业银行旧址全国重点文物保护单位中华人民共和国国务院公布地址天津市和平区坐标39°7′43.028″N 117°12′13.428″E / 39.12861889°N 117.20373000°E / 39.12861889; 117.20373000分类近现代重要史迹及代表性建筑时代民国编号6-889认定时间2006年5月25日 盐业银行旧址,建于1928年,当时为盐业银行的总部大楼,坐落于当时天津法租界的水师营路(Rue de L'Amiraute)(今和平区赤...

GreensboroughStasiun komuter PTVLokasiPara Road, GreensboroughMelbourne, VictoriaAustraliaKoordinat37°42′14″S 145°06′29″E / 37.7040°S 145.1081°E / -37.7040; 145.1081Koordinat: 37°42′14″S 145°06′29″E / 37.7040°S 145.1081°E / -37.7040; 145.1081PemilikVicTrackOperatorMetro TrainsJalur HurstbridgeJumlah peron2Jumlah jalur2KonstruksiJenis strukturTanahParkir212Fasilitas sepedaYaInformasi lainZona tarifMyki Zona 2Sit...

Iranian actress and film director (born 1984) Pegah Ahangaraniپگاه آهنگرانیAhangarani at the 35th Fajr Film Festival (2017)BornPegah Ahangarani Farahani (1984-07-24) 24 July 1984 (age 39)Arak, IranOccupationsActressfilm directorYears active1990–presentParentsJamshid Ahangarani (father)Manijeh Hekmat (mother) Pegah Ahangarani (Persian: پگاه آهنگرانی; born 24 July 1984) is an Iranian actress and director. She has received various accolades, including a Crysta...

Anna Lee Anna Lee, nata Joan Boniface Winnifrith (Ightham, 2 gennaio 1913 – Beverly Hills, 14 maggio 2004), è stata un'attrice britannica naturalizzata statunitense. Indice 1 Biografia 2 Filmografia parziale 2.1 Cinema 2.2 Televisione 3 Doppiatrici italiane 4 Altri progetti 5 Collegamenti esterni Biografia La famiglia di Anna Lee contava numerosi membri del clero, compreso il padre, che sostenne sempre la figlia nel suo desiderio di diventare attrice. Il secondo nome Boniface venne scelto ...












