Grande rombiesaedro
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Hugh FordHugh Ford pada 1919Lahir5 Februari 1868Washington, D.C., Amerika SerikatMeninggal1952 – 1868; umur -85–-84 tahunPekerjaanSutradara, penulis naskahTahun aktif1913-1921 Hugh Ford (5 Februari 1868 – 1952) adalah seorang sutradara dan penulis naskah Amerika Serikat. Ia menyutradarai 31 film antara 1913 dan 1921. Ia juga menulis untuk 19 film antara 1913 dan 1920.[1] Referensi ^ Hugh Ford, biography, allmovie.com Pranala luar Wikimedia Commons memiliki...

MunduKecamatanNegara IndonesiaProvinsiJawa BaratKabupatenCirebonPemerintahan • CamatH. Anwar Sadat, S.Sos, M.SiPopulasi • Total76.856 jiwaKode Kemendagri32.09.12 Kode BPS3209090 Luas27,47 km²Desa/kelurahan12 Untuk kegunaan lain, lihat Mundu. Mundu adalah sebuah kecamatan di Kabupaten Cirebon, Provinsi Jawa Barat, Indonesia. Kecamatan ini terletak pada bagian timur Kota Cirebon. Kecamatan ini sempat mengajukan diri untuk bergabung kedalam Kota Cirebon.[1] ...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

FlickrURLFlickr.comTipeFoto Video Jejaring foto dan videoPerdagangan ?YaLangueInggris Cina Prancis Jerman Italia Portugis Bahasa Spanyol Korea IndonesiaBagian dariSmugMug PemilikYahoo! Inc.PembuatLudicorpWeb DeveloperSmugMug, Ludicorp dan Yahoo! (perusahaan) Service entryFebruari 2004Tempat pembentukanVancouver Lokasi kantor pusatSan Francisco Peringkat Alexa 30[1] KeadaanAktifBlog resmihttps://blog.flickr.net Flickr adalah situs web untuk berbagi foto dan situs komunitas daring ...

Hotel chain based in North America Aloft HotelsCompany typeFranchiseIndustryhospitalityFounded2005FounderW HotelsNumber of locations233[1] (April 2023)Area servedUnited States, Canada, Europe, AsiaOwnerMarriott InternationalParentMarriott InternationalWebsitealoft-hotels.marriott.com Aloft Hotels is an American hotel chain based in North America, owned by Marriott International. The first hotel opened at the Trudeau International Airport in Montreal in 2008.[2] Aloft Hote...

Перуанский анчоус Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёрые �...

2017 horror film The CrucifixionPosterDirected byXavier GensWritten byChad HayesCarey W. HayesProduced byLeon ClarancePeter SafranStarringSophie CooksonBrittany AshworthCorneliu UliciCinematographyDaniel AranyóEdited byAdam TrotmanMusic byDavid JulyanProductioncompaniesLotus EntertainmentMotion Picture CapitalPoznan Film GroupPremiere PictureThe Safran CompanyDistributed byGrindstone Entertainment GroupLionsgateRelease date October 6, 2017 (2017-10-06) Running time90 minutesCo...

1993 song by U2 ZooropaMexico promotional releasePromotional single by U2from the album Zooropa Released5 July 1993 (1993-07-05)RecordedMarch–May 1993StudioWindmill Lane Studios (Dublin)The Factory (Dublin)GenreAlternative rockLength6:304:42 (edit)LabelIslandComposer(s)U2Lyricist(s)BonoProducer(s)FloodBrian EnoThe EdgeAudio samplefilehelp Zooropa is a song by Irish rock band U2, and is the opening track from their 1993 album of the same name. The song was the result of combin...

† Египтопитек Реконструкция внешнего вида египтопитека Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:Четвероно...

This article is about the mythological figure in the Andes Region. For other uses, see Muki. This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2013) (Learn how and when to remove this message) The muki (Quechua for asphyxia, also for a goblin who lives in caves,[1] also spelled muqui or mooqui) is a goblin-like creature in the mythology of the...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يونيو 2022) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسي...
Town in New South Wales, AustraliaDilpurraNew South WalesDilpurraLocation in New South WalesCoordinates35°12′S 143°42′E / 35.200°S 143.700°E / -35.200; 143.700Population29 (SAL 2021)[1]Postcode(s)2734Location 57 km (35 mi) from Moulamein 15 km (9 mi) from Swan Hill LGA(s)Murray River CouncilCountyWakoolState electorate(s)MurrayFederal division(s)Farrer Dilpurra is a village community in the south western part of the Riverina in New ...

Airport in Kazakhstan This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Pavlodar Airport – news · newspapers · books · scholar · JSTOR (May 2013) (Learn how and when to remove this message) Pavlodar AirportPavlodar Halyqaralyq Äuejaiy (Kazakh)IATA: PWQICAO: UASPSummaryAirport typePublicOwnerSamruk-Kazyna...
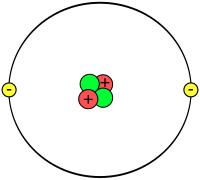
Unit of length (10^-12 meters) For examples of things measuring between one and ten picometres, see 1 picometre. PicometreA simplified representation of a helium atom, having an estimated (calculated) diameter of 62 picometres[1]General informationUnit systemSIUnit oflengthSymbolpmConversions 1 pm in ...... is equal to ... SI base units 1×10−12 m Natural units 6.1877×1022 ℓP ...

1965 American Civil War film directed by Andrew V. McLaglen This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Shenandoah film – news · newspapers · books · scholar · JSTOR (June 2015) (Learn how and when to remove this message) Shenandoah1965 cinema posterDirected byAndrew V. McLaglenScreenplay byJames Le...

Ship with no living people onboard This article is about vessels with no living crew aboard. For other uses, see Ghost ship (disambiguation). The mysteriously derelict schooner Carroll A. Deering, as seen from the Cape Lookout lightship on 28 January 1921 (US Coast Guard) A ghost ship, also known as a phantom ship, is a vessel with no living crew aboard; it may be a fictional ghostly vessel, such as the Flying Dutchman, or a physical derelict found adrift with its crew missing or dead, l...

قبر الامام الطبري في حديقة الرحبي 2017 حديقة الرحبي (أو رحبة يعقوب)، هي حديقة عامة،[1] كبيرة واسعة المساحة تبلغ مساحتها حوالي عشرة آلاف متر مربع تقريبا، في شارع عشرين في المحلة 314 في حي الأعظمية،[2] تقع الحديقة في جانب الرصافة من بغداد عاصمة العراق.[3] كانت مقصداً لتن...

Dark Horse Comics Stand de Dark Horse Comics en el WonderCon de 2010.Tipo Empresa independienteIndustria EditorialGénero Acción, Ciencia ficción, Bélica, Terror, Fantasía, AventurasForma legal editorialFundación 1986Fundador Mike RichardsonSede central Milwaukie, Oregón, Estados UnidosProductos CómicsPropietario Embracer GroupEmpresa matriz Dark Horse MediaFiliales Berger BooksSitio web darkhorse.com[editar datos en Wikidata] Dark Horse Comics es una editorial independiente ...

2018 AFF Women's ChampionshipTournament detailsHost country IndonesiaCityPalembangDates30 June – 13 JulyTeams10 (from 1 sub-confederation)Venue(s)2 (in 1 host city)Final positionsChampions Thailand (4th title)Runners-up Australia U20Third place VietnamFourth place MyanmarTournament statisticsMatches played24Goals scored154 (6.42 per match)Attendance2,600 (108 per match)Top scorer(s) Mary Fowler (10 goals)← 2016 2019 → Internation...

Main article: 1976 United States presidential election 1976 United States presidential election in West Virginia ← 1972 November 2, 1976 1980 → Nominee Jimmy Carter Gerald Ford Party Democratic Republican Running mate Walter Mondale Bob Dole Electoral vote 6 0 Popular vote 435,914 314,760 Percentage 58.07% 41.93% County Results Carter 50–60% 60–70% 70–80% Ford 50–60% 60–70% ...













