Grande dodecicosaedro

Tipo

Poliedro stellato uniforme

Forma facce

20 esagoni
12 decagrammi

Nº facce

Nº spigoli

120

Nº vertici

Caratteristica di Eulero

-28

Incidenza dei vertici

6.¹⁰/₃.⁶/₅.¹⁰/₇

Notazione di Wythoff

3 ⁵/₃ (³/₂ ⁵/₂) |

Diagramma di Coxeter-Dynkin

Gruppo di simmetria

I_h, [5,3], *532

Duale

Grande dodecicosacrono

Proprietà

Politopi correlati

In geometria, il grande dodecicosaedro è un poliedro stellato uniforme avente 32 facce - 20 esagonali e 12 forma di decagramma - 120 spigoli e 60 vertici.^[1]

Costruzioni di Wythoff

Utilizzando la costruzione di Wythoff, il grande dodecicosaedro si può ottenere utilizzando tre famiglie di triangoli di Schwarz: 3 5/3 3/2 | e 3 5/3 5/2 |, ottenendo sempre lo stesso risultato.

Coordinate cartesiane

Le coordinate cartesiane per i vertici del grande dodecicosaedro sono date da tutte le permutazioni pari di:

\left(\,\pm 1,\,\pm 2(\varphi -1),\,\pm \varphi \,\right)

\left(\,0,\,\pm (2-\varphi ),\,\pm {\sqrt {5}}\,\right)

\left(\,\pm 1,\,\pm 2,\,\pm (2-\varphi )\,\right)

dove $\varphi ={\tfrac {1+{\sqrt {5}}}{2}}$ è la sezione aurea.

Poliedri correlati

Il grande dodecicosaedro, spesso indicato con il simbolo U₆₃, ha la stessa disposizione di vertici del dodecaedro troncato, una cui versione non regolare è il suo inviluppo convesso, e condivide la posizione degli spigoli con il grande dodecicosidodecaedro ditrigonale, con cui ha in comune la disposizione delle facce decagrammiche, e con il grande icosicosidodecaedro, con cui ha in comune la disposizione delle facce esagonali.

Dodecaedro troncato	Grande icosicosidodecaedro	Grande dodecicosidodecaedro ditrigonale	Grande dodecicosaedro

Grande dodecicosacrono

Grande dodecicosacrono

Tipo	Poliedro stellato
Forma facce	Antiparallelogrammi
Nº facce	60
Nº spigoli	120
Nº vertici	32
Caratteristica di Eulero	-28
Gruppo di simmetria	I_h, [5,3], *532
Duale	Grande dodecicosaedro
Manuale

Il grande dodecicosacrono è un poliedro stellato isoedro, nonché il duale del grande dodecicosaedro, avente per facce 60 antiparallelogrammi.^[2] Dato un grande dodecicosaedro di spigolo pari a 1, immaginando il grande dodecicosacrono come composto da 60 facce intersecanti a forma di antiparalleogramma, come riportato nella figura sottostante, di cui solo una parte visibile all'esterno del solido, le facce risultanti hanno due coppie di angoli uguali di ampiezza pari a $\arccos({\frac {3}{4}}+{\frac {1}{20}}{\sqrt {5}})\approx 30,480\,324\,565\,36^{\circ }$ e $\arccos(-{\frac {5}{12}}+{\frac {1}{4}}{\sqrt {5}})\approx 81,816\,127\,508\,183^{\circ }$ , con il rapporto tra lati lunghi e lati corti pari a ${\frac {1}{2}}+{\frac {1}{2}}{\sqrt {5}}$ , e le due diagonali che si incontrano con un angolo di $\arccos({\frac {5}{12}}-{\frac {1}{60}}{\sqrt {5}})\approx 67,703\,547\,926\,46^{\circ }$ .

Note

^ Roman Maeder, 63: great dodecicosahedron, su Mathconsult. URL consultato il 24 marzo 2024.
^ Magnus J. Wenninger, Dual Models, Cambridge University Press, 2004, pp. 67. URL consultato il 20 marzo 2024.

Collegamenti esterni

(EN) Eric W. Weisstein, Grande dodecicosaedro, su MathWorld, Wolfram Research.
(EN) Eric W. Weisstein, Grande dodecicosacrono, in MathWorld, Wolfram Research. URL consultato il 20 marzo 2024.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica

Read other articles:

Daftar pembawa bendera Norwegia pada Olimpiade

Norwegia padaOlimpiadeKode IOCNORKONKomite Olimpiade dan Konfederasi Olahraga NorwegiaSitus webwww.idrettsforbundet.no (dalam bahasa Norwegia)Medali 188 174 158 Total 520 Penampilan Musim Panas1900190419081912192019241928193219361948195219561960196419681972197619801984198819921996200020042008201220162020Penampilan Musim Dingin192419281932193619481952195619601964196819721976198019841988199219941998200220062010201420182022Penampilan terkait lainnyaOlimpiade Interkala 1906 Berikut...

Klaim teritorial di Arktik

Topografi dan batimetri Arktik Arktik terdiri dari daratan, perairan pedalaman, laut teritorial, Zona Ekonomi Eksklusif (ZEE) dan Perairan internasional di atas Lingkaran Arktik (66 derajat 33 menit Lintang Utara). Semua daratan, perairan pedalaman, laut teritorial, dan ZEE di Arktik berada di bawah yurisdiksi salah satu dari delapan negara pesisir Arktik: Kanada, Denmark (melalui Greenland), Finlandia, Islandia, Norwegia, Rusia, Swedia, dan Amerika Serikat.[1] Di bawah hukum internas...

The Librarians (film)

2001 film by Mike Kirton The LibrariansDirected byMike KirtonWritten by William Forsythe Mike Kirton Produced byGreg HauptnerStarring William Forsythe Andrew Divoff Erika Eleniak Christopher Atkins CinematographyGary B. KibbeEdited byRinaldo MarsiliMusic byJohn PrattProductioncompanyGlobal PicturesRelease date December 16, 2003 (2003-12-16) Running time96 minutesCountryUnited StatesLanguageEnglishBudget$4 million[1] The Librarians (also known as Strike Force) is a 2003 ...

Joshua Friedel

American chess player Joshua FriedelFriedel at the American Continental Chess Championship in Toluca, April 2011Full nameJoshua E. FriedelCountryUnited StatesBorn (1986-12-03) December 3, 1986 (age 37)Goffstown, New Hampshire, U.S.TitleGrandmaster (2008)FIDE rating2552 (March 2024)Peak rating2562 (January 2018) Joshua E. Friedel[1] (born December 3, 1986) is an American chess player with the FIDE title of Grandmaster. He was the U.S. Open Champion in 2013.[2 ...

John E. Miller

American judge For the state representative, see John E. Miller (Arkansas politician). For the U.S. Army general, see John E. Miller (general). John E. MillerSenior Judge of the United States District Court for the Western District of ArkansasIn officeFebruary 28, 1967 – January 30, 1981Chief Judge of the United States District Court for the Western District of ArkansasIn office1958–1967Preceded byHarry Jacob LemleySucceeded byOren HarrisJudge of the United States District Court ...

Khloé Kardashian

American media personality (born 1984) Khloé KardashianKardashian in 2016BornKhloe Alexandra Kardashian[a] (1984-06-27) June 27, 1984 (age 39)Los Angeles, California, U.S.Other namesKhloé Kardashian OdomEducationMarymount High SchoolOccupations Media personality socialite model Years active2007–presentSpouse Lamar Odom (m. 2009; div. 2016)Partner(s)Tristan Thompson(2016–2021)Children2Parents Robert Kardashian (fa...

Spanish expedition to Balanguingui

1848 amphibious campaign Balanguingui ExpeditionPart of piracy in AsiaNaval bombardment of Balanguingui, by Fernández Muñoz.Date16–22 February 1848LocationBalanguingui Island, the Philippines.Result Spanish victoryBelligerents Captaincy General of the Philippines Moro PiratesCommanders and leaders Narciso Clavería y Zaldúa unknownStrength 19 warships Land:~1,000 pirates124 artillery pieces4 fortsSea:~150 proasCasualties and losses 229-237 killed or wounded[1] ~450 killed6 captur...

Asa Hodges

American politician (1822–1900) This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (March 2013) (Learn how and when to remove this message) Asa HodgesAsa HodgesMember of the U.S. House of Representativesfrom Arkansas's 1st districtIn officeMarch 4, 1873 – March 3, 1875Preceded byJames M. HanksSucceeded b...

コルク

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方）出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL（2017年4月）コルクを打ち抜いて作った瓶の栓コルク（木栓、�...

Natation synchronisée

Natation synchroniséeNatation artistique Données clés Fédération internationale Fédération internationale de natation (FINA) Sport olympique depuis 1984 Équipe technique française, à l'Open Make Up For Ever de 2013 (Montreuil). modifier La natation synchronisée, appelée officiellement natation artistique[1],[2] depuis l'été 2017, est un sport nautique, mélange de gymnastique, de danse et de natation qui se pratique en piscine. Discipline très exigeante et complexe, elle deman...

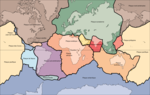
Plaque arabique

Pour les articles homonymes, voir Arabie (homonymie). Plaque arabique Éponyme Arabie Composition Lithosphère océanique et continentale Frontières Dorsale de la mer Rouge Superficie 0,12082 stéradians Déplacement · Direction : · Vitesse : nord-est4,65 cm/an(référentiel : plaque africaine) Rotation · Vitesse : · Pôle eulérien : 1,161 6 °/Ma59° 66' N 33° 19' O(référentiel : plaque pacifique) modifier La plaque arabique est un...

Grosseto Baseball

Jolly Roger Grosseto BaseballBaseball Segni distintiviUniformi di gara Casa Trasferta Colori sociali Bianco e rosso SimboliGrifone Dati societariCittàGrosseto Nazione Italia ConfederazioneCEB FederazioneFIBS CampionatoSerie A Fondazione1952 Rifondazione2012 Rifondazione2017 Presidente Giuseppe Demi Allenatore Jairo Ramos Gizzi Sito webhttp:// Palmarès Scudetti4 Coppe Italia3 Coppe dei Campioni1 Coppe CEB1 Altri titoli1 Scudetto Serie A Federale Impianto di gioco Stadio Roberto Jannella...

University of Waikato

Public university in Hamilton, New Zealand A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (February 2018) (Learn how and when to remove this message) University of WaikatoTe Whare Wānanga o WaikatoCoat of Arms of the University of WaikatoMottoMāori: Ko te tangataMotto in EnglishFor The PeopleTypePublic...

最終幻想 (音樂專輯)

最終幻想古巨基的录音室专辑发行日期2005年12月2日录制时间2005年类型國語时长45分52秒唱片公司金牌娛樂古巨基专辑年表星战（2005年）星战2005 最終幻想（2005年） Human我生（2006年）Human我生2006 《最終幻想》是香港歌手古巨基的流行音樂專輯，於2005年12月2日正式發行。簡介繼2005年3月在紅館舉行的《05勁歌金曲演唱會PART ONE/ TWO》後，古巨基馬不停蹄地工作，與楊千嬅等到�...

Puttingal Temple

Hindu temple in Kerala, India This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Puttingal Temple – news · newspapers · books · scholar · JSTOR (April 2016) (Learn how and when to remove this message) Puttingal TempleParavur Puttingal Devi TemplePuttingal temple festivalReligionAffiliationHinduismDistrictKollam...

نادي كالياري

كالياري كالشيو الاسم الكامل نادي كالياري لكرة القدم اللقب روزوبلو (الأحمر والأزرق إسولاني (جزيريون) تأسس عام 1920 (منذ 104 سنوات) الملعب ملعب سانت إلياكالياري - إيطاليا(السعة: 23,486) البلد إيطاليا الدوري الدوري الإيطالي الإدارة الرئيس ماسيمو تشيلينو المدرب كلاوديو رانيير...

Shuja'iyya

Neighborhood in Gaza, Gaza Governorate, PalestineShuja'iyya الشجاعيةNeighborhoodShuja'iaShuja'iyyaLocation in Gaza StripCoordinates: 31°30′02″N 34°28′12″E / 31.50056°N 34.47000°E / 31.50056; 34.47000Country PalestineGovernorateGaza GovernorateCityGazaTime zoneUTC+2 (EET) • Summer (DST)+3 Shuja'iyya (Arabic: الشجاعية), also Shejaiya, Shijaiyeh, Shujayya, Shuja'ia, Shuja'iya, is a neighborhood district of the Palestinian city ...

José David Name

Colombian politician José David NameA Colombian senatorPresident of the SenateIn office20 July 2014 – 20 July 2015Preceded byJuan Fernando CristoSucceeded byLuis Fernando VelascoSenator of ColombiaIncumbentAssumed office 20 July 2006 Personal detailsBorn (1968-11-18) 18 November 1968 (age 55)Barranquilla, Atlántico, ColombiaPolitical partySocial Party of National UnitySpouseAstrid CorreaRelationsJosé Name Terán (father)Iván Name Vásquez (cousin)Alma materAutonomous U...

Billboard China

Chinese Internet musical publication Billboard ChinaBillboard China logoType of siteOnline magazineAvailable inChineseOwnerVision Media GroupURLbillboardchina.cnCommercialYesRegistrationNoneLaunchedSeptember 5, 2016; 7 years ago (2016-09-05)Current statusActive Billboard China (simplified Chinese: 中国公告牌; traditional Chinese: 中國公告牌) was a Chinese online music magazine founded by Vision Media Group on September 5, 2016.[1] It serve...

Diamond Princess (tàu)

Cảnh báo: Tên hiển thị “Diamond Princess (tàu)” ghi đè tên hiển thị “<i>Diamond Princess</i> (tàu)” bên trên. Diamond Princess cập cảng Hobart, Australia Lịch sử Vương quốc Anh Tên gọi Diamond PrincessChủ sở hữu Carnival Corporation & plcBên khai thác Princess CruisesCảng đăng ký 2004 – 2014: Hamilton, Bermuda Từ 2014: Luân Đôn, Vương quốc Anh Xưởng đóng tàu Mitsubishi Heavy IndustriesKinh ...