Grande dodecaemicosaedro

Grande dodecaemicosaedro
TipoPoliedro stellato uniforme
Forma facce12 pentagoni
10 esagoni
Nº facce22
Nº spigoli60
Nº vertici30
Caratteristica di Eulero-8
Incidenza dei vertici5.6.5/4.6
Notazione di Wythoff5/4 5 | 3
Diagramma di Coxeter-Dynkin
Gruppo di simmetriaIh, [5,3], *532
DualeGrande dodecaemicosacrono
ProprietàNon convessità
Politopi correlati
Figura al vertice
Poliedro duale
Manuale

In geometria, un grande dodecaemicosaedro è un poliedro stellato uniforme, e in particolare un emipoliedro, avente 22 facce - 12 pentagonali e 10 esagonali - 60 spigoli e 30 vertici.

Proprietà

La figura al vertice di questo poliedro, che viene spesso indicato con il simbolo U65, ha la forma di un quadrilatero incrociato.
Utilizzando la notazione di Wythoff, il grande dodecaemicosaedro può essere indicato come "5/4 5 | 3".

Come detto, il grande dodecaemicosaedro appartiene all'insieme degli emipoliedri, ossia poliedri stellati uniformi aventi alcune delle facce passanti per il proprio centro e così chiamati perché in essi tali facce formano un gruppo contenente la metà degli stessi elementi presenti in un poliedro regolare e disposti come in esso, da cui il prefisso "emi-". In particolare, nel grande dodecaemicosaedro tale gruppo è formato dalle sue dieci facce esagonali, tutte passanti per il suo centro.

Poliedri correlati

Il grande dodecaemicosaedro, il cui inviluppo convesso è un icosidodecaedro, ha gli stessi vertici e gli stessi spigoli di un dodecadodecaedro, con cui ha in comune anche la disposizione delle facce pentagonali, e di un piccolo dodecaemicosaedro, con cui ha in comune anche la disposizione delle facce esagonali.


Dodecadodecaedro
Piccolo dodecaemicosaedro
Grande dodecaemicosaedro

Icosidodecaedro

Grande dodecaemicosacrono

Grande dodecaemicosacrono
TipoPoliedro stellato
Nº facce30
Nº spigoli60
Nº vertici22
Caratteristica di Eulero-8
Gruppo di simmetriaIh, [5,3], *532
DualeGrande dodecaemicosaedro
Manuale

Il grande dodecaemicosacrono è il duale del grande dodecaemicosaedro, nonché uno dei nove emipoliedri duali esistenti.

Poiché gli emipoliedri hanno facce passanti per il loro centro, i loro duali hanno vertici posti all'infinito, e più precisamente all'infinito sul piano proiettivo reale.[1] Nella sua opera "Dual Models", Magnus Wenninger rappresenta tali figure come prismi intersecanti, ognuno dei quali si estende all'infinito verso il vertice stesso, così da mantenere la simmetria. Nella comune rappresentazione i prismi costituenti il modello vengono per comodità tagliati a un certo punto della loro altezza. Wenninger ha suggerito di inserire queste nuove figure in una nuova classe di solidi generati per stellazione, chiamati "stellazioni all'infinito". Tuttavia egli ha anche affermato che, strettamente parlando, tali figure non sarebbero in effetti poliedri poiché la loro costruzione non risulta conforme alle comuni definizioni.[1]

Topologicamente, si considera che il grande dodecaemicosacrono, che visivamente appare identico al piccolo dodecaemicosacrono, contenga 22 vertici, dieci dei quali sono considerati all'infinito (sul piano proiettivo reale all'infinito) e corrispondono direzionalmente ai sei vertici di un emicosaedro, un poliedro astratto.

Note

  1. ^ a b Magnus Wenninger, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 730208.

Collegamenti esterni

  Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica

Read other articles:

The Property Man

The Property ManPoster teatrikal untuk The Property ManSutradaraCharlie ChaplinProduserMack SennettPemeranCharles ChaplinPhyllis AllenAlice DavenportCharles BennettMack SennettNorma NicholsJoe BordeauxHarry McCoyLee MorrisSinematograferFrank D. WilliamsPerusahaanproduksiKeystone StudiosDistributorMutual FilmTanggal rilis 01 Agustus 1914 (1914-08-01) Durasi31 menitNegaraAmerika SerikatBahasaFilm bisuInggris (titel asli) The Property Man The Property Man adalah sebuah film bisu komedi pend...

 

 

Kekayaan budaya

Plakat Bundesdenkmalamt di sebuah gedung di Salzburg yang menunjukkan Kekayaan budaya dalam empat bahasa; Jerman: Kulturdenkmal, Inggris, Prancis: Bien culturel, dan Rusia: Культурное Достояние. Kekayaan budaya atau cagar budaya (istilah lebih spesifik dalam perundang-undangan Indonesia) adalah sebuah benda fisik yang merupakan bagian dari warisan budaya suatu kelompok atau masyarakat.[1] Barang-barang tersebut termasuk bangunan bersejarah, karya seni, situs arkeolo...

 

 

Papal election of Giuseppe Siri theory

Traditionalist Catholic conspiracy theory Giuseppe Siri in 1958 Some hold the conspiracy theory which asserts that the conservative Cardinal Giuseppe Siri, then the Archbishop of Genoa, was elected pope in the 1958 papal conclave, taking the name Pope Gregory XVII, but that his election was suppressed. Siri did not associate himself with this idea. Its exponents claim that a prolonged emission of white smoke on the first day of balloting at the conclave indicated the election of Siri, but tha...

Passerelle Debilly

Bridge in Paris, France Passerelle DebillyCoordinates48°51′45.56″N 02°17′48.68″E / 48.8626556°N 2.2968556°E / 48.8626556; 2.2968556CarriesPedestriansCrossesSeineLocaleParis, FranceOfficial namePasserelle DebillyMaintained byCivil ServiceNext upstreamPont de l'AlmaNext downstreamPont d'IénaCharacteristicsDesignThrough arch bridgeTotal length125 m (410 ft)Width8 m (26 ft)HistoryOpened1900Location Passerelle Debilly from Pont d'Iéna The Passerelle Debilly ('...

 

 

Panthéon

Mausoleum in Paris for the most distinguished French people Not to be confused with Pantheon, Rome. For other uses of Pantheon, see Pantheon (disambiguation). PanthéonThe PanthéonFormer namesÉglise Sainte-GenevièveGeneral informationTypeMausoleumArchitectural styleNeoclassicismLocationPlace du PanthéonParis, FranceCoordinates48°50′46″N 2°20′45″E / 48.84611°N 2.34583°E / 48.84611; 2.34583Construction started1758Completed1790Design and constructionArchit...

 

 

趙家驤

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)（47—48歲） † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章（追贈）军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年－1958年军衔 二級上將 （追晉）部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

Platì

Platìcomune Platì – Veduta LocalizzazioneStato Italia Regione Calabria Città metropolitana Reggio Calabria AmministrazioneSindacoRosario Sergi (lista civica) dal 22-9-2020 TerritorioCoordinate38°13′N 16°03′E / 38.216667°N 16.05°E38.216667; 16.05 (Platì)Coordinate: 38°13′N 16°03′E / 38.216667°N 16.05°E38.216667; 16.05 (Platì) Altitudine300 m s.l.m. Superficie50,87 km² Abitanti3 704[1]&...

 

 

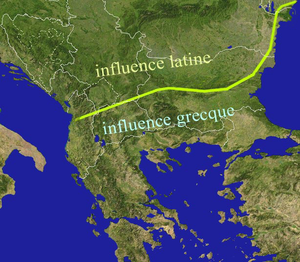
Ligne Jireček

La « ligne Jireček » La ligne Jireček est une ligne passant à travers les Balkans antiques, définie par l'historien tchèque Konstantin Jiřeček en 1911 dans son Histoire des Serbes, pour délimiter les influences du latin (au nord) et du grec (au sud) jusqu'au IVe siècle. Description La ligne Jiřeček, fondée sur les découvertes archéologiques, suit le tracé au sud duquel les inscriptions en grec dominent, tandis qu'au nord ce sont celles en latin. Elle part de la...

 

 

Carlo Pergamo

Carlo Pergamovescovo della Chiesa cattolica  Incarichi ricopertiVescovo di Gaeta (1771-1785)  Nato4 novembre 1726 a Napoli Ordinato presbitero20 dicembre 1749 Nominato vescovo16 dicembre 1771 da papa Clemente XIV Consacrato vescovo21 dicembre 1771 dal cardinale Ludovico Calini Deceduto26 giugno 1785 (58 anni) a Gaeta   Manuale Carlo Pergamo (Napoli, 4 novembre 1726 – Napoli, 26 giugno 1785) è stato un vescovo cattolico italiano. Indice 1 Biografia 1.1 Formazione e minis...

My Jackhammer

2003 studio album by Benevento/Russo DuoMy JackhammerStudio album by Benevento/Russo DuoReleasedJanuary 1, 2003Recorded2002GenreAcid Jazz, RockBenevento/Russo Duo chronology My Jackhammer(2003) Darts(2003) My Jackhammer is the debut album from the Benevento/Russo Duo, released in 2003 under their own production. Track listing Raindrops Whisper Words - 9:21 Sabia - 7:00 Improv I - 12:32 Seeup, Seedown - 4:22 Improv II - 10:11 My Jackhammer - 16:38 Curvedspace - 6:01 Impact - 6:29 Redbu...

 

 

Mayotte

Overseas department of France in the Indian Ocean Mahore redirects here. For the main island of the department, see Grande-Terre (Mayotte). Place in FranceMayotteOverseas department, region and single territorial collectivity of France and outermost region of the European UnionDepartment of MayotteDépartement de Mayotte (French) Coat of armsAnthem: La Marseillaise(The Marseillaise)Coordinates: 12°50′35″S 45°8′18″E / 12.84306°S 45.13833°E / -12.84306; ...

 

 

Dimethylallyl pyrophosphate

Dimethylallyl pyrophosphate Names IUPAC name 3-Methyl-2-buten-1-yl trihydrogen diphosphate Other names Dimethylallyl diphosphate; isoprenyl pyrophosphate; isoprenyl diphosphate Identifiers CAS Number 358-72-5 Y 3D model (JSmol) Interactive image ChemSpider 627 Y MeSH 3,3-dimethylallyl+pyrophosphate PubChem CID 647 CompTox Dashboard (EPA) DTXSID70189331 InChI InChI=1S/C5H12O7P2/c1-5(2)3-4-11-14(9,10)12-13(6,7)8/h3H,4H2,1-2H3,(H,9,10)(H2,6,7,8)Key: CBIDRCWHNCKSTO-UHFFFAOYSA-N SM...

List of cities besieged by the Ottoman Empire

Siege of Constantinople,1453 Siege of Rhodes, 1480 Siege of Eger Castle, 1552 Great Siege of Malta, 1565 Below is the list of cities which were besieged by the Ottoman Empire. Year City State Modern City Modern state 1285 Kulaca Hisar Byzantine Empire İnegöl Turkey 1326 Prusa Byzantine Empire Bursa Turkey 1331 Nicaea Byzantine Empire Iznik Turkey 1337 Nicomedia Byzantine Empire Izmit Turkey 1361 Adrianople Byzantine Empire Edirne Turkey 1393 Tarnovo Bulgarian Empire Veliko Tarnovo Bulgaria...

 

 

تاريخ بغداد 1831-1917

بغداد تاريخ بغداد 1831-1917 1831 – 1917 بغداد في يوم 11 أذار - مارس من سنة 1917 م عاصمة بغداد نظام الحكم ولاية الوالي علي رضا باشا 1842-1831 مدحت باشا 1872-1869 جمال باشا 1912-1911 خليل باشا (الأخير) 1917-1915 التاريخ التأسيس 1831 الزوال 1917 اليوم جزء من  العراق تعديل مصدري - تعديل   بغداد في عام 1917 ...

 

 

Liste des circonscriptions législatives de l'Ardèche

Le département français de l'Ardèche est, sous la Cinquième République, constitué de trois circonscriptions législatives, ce nombre étant stable depuis 1958. Leurs limites ont été redéfinies lors du redécoupage de 1986, mais n'ont pas été affectées par celui de 2010, en vigueur à compter des élections législatives de 2012. Présentation Par ordonnance du 13 octobre 1958 relative à l'élection des députés à l'Assemblée nationale, le département de l'Ardèche est constit...

Roderic

8th-century king of the Visigoths For the given name, see Roderick. RodericRoderic depicted as one of the six kings in an Umayyad fresco in Qasr Amra, modern-day Jordan, from between 710 and 750.[1] Roderic is the second figure, his face completely lost, with only the tip of his helmet and his robes being visible.[2]King of the VisigothsReign710 – July 711PredecessorWittizaSuccessorAchila IIDiedJuly 711Visigothic KingdomSpouseEgilona Roderic (also spelled Ruderic, Roderik, R...

 

 

Valle Salimbene

Questa voce o sezione sull'argomento centri abitati della Lombardia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Valle Salimbenecomune LocalizzazioneStato Italia Regione Lombardia Provincia Pavia AmministrazioneSindacoVelea Daniela Maria Gatti Comini (lista civica) dall'8-6-2009 Te...

 

 

Seljuk Empire

Turco-Persian Sunni Muslim empire (1037–1194) This article contains several duplicates of the same citations. The reason given is: DuplicateReferences detected: http://www.iranicaonline.org/articles/sahrbanu (refs: 17, 70, 72) https://www.metmuseum.org/art/metpublications/Court_and_Cosmos (refs: 166, 168) https://cdn.islamansiklopedisi.org.tr/dosya/25/C25008111.pdf (refs: 178, 212) https://islamansiklopedisi.org.tr/musa-yabgu (refs: 183, 206) https://cdn.islamansiklopedisi.org.tr/dosya/26/C...

رسائل الكاثوليكون

هي مجموعة من أسفار العهد الجديد التي سميت بالكاثوليكون Catholicon أي الجامعة وتعرف أيضا بالعامة، وهذا التعريف ليس دقيقًا كما يراه بعض دارسي الكتاب المقدس، فرغم أنها ليست كرسائل بولس الرسول الذي كتب أصلاً للكنائس ولأشخاص فهذه الرسائل كتبت إلى المسيحيين المتشتتين والذين هم من �...

 

 

3rd Rock from the Sun season 3

Season of television series 3rd Rock from the SunSeason 3DVD coverNo. of episodes27ReleaseOriginal networkNBCOriginal releaseSeptember 24, 1997 (1997-09-24) –May 20, 1998 (1998-05-20)Season chronology← PreviousSeason 2Next →Season 4List of episodes The third season of 3rd Rock from the Sun, an American television series, began September 24, 1997, and ended on May 20, 1998. It aired on NBC. The region 1 DVD was released on February 21, 2006.[1] Cast and ...