|
Funzione test (ottimizzazione)
Le funzioni test sono delle funzioni pensate e utilizzate per testare il funzionamento e l'efficienza degli algoritmi di ottimizzazione. Gli aspetti dell'algoritmo che tipicamente interessa mettere alla prova sono la velocità di convergenza, la precisione del risultato e la robustezza dell'algoritmo. Le funzioni test sono spesso problemi artificiali che mettono alla prova gli algoritmi in situazioni particolarmente scomode, ad esempio nella ricerca di minimi in funzioni particolarmente piatte (come un punto di minimo di una funzione continua nel quale si annullano molte derivate successive), funzioni il cui comportamento globale approssima quello di una funzione unimodale ma che in realtà presenta altri estremi locali, funzioni con un gran numero di punti di ottimo locali significativi, o funzioni il cui andamento globale non fornisce indicazioni significative sulla posizione dei punti di ottimo.[1]
Nel seguito sono riportate alcune tra le più note funzioni test con una espressione in forma generale e le loro principali caratteristiche.
Principali funzioni test
Le funzioni test presentate nel seguito sono riportate in Bäck,[2] Haupt et. al.[3] e dalla libreria software di Rody Oldenhuis.[4]
| Nome |
Grafico |
Espressione |
Minimo |
Dominio di ricerca
|
| Funzione di Ackley
|
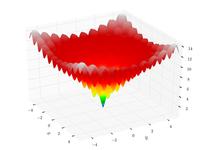
|


|

|

|
| Funzione sferica
|
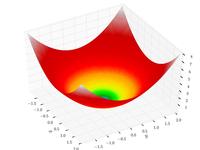
|

|

|
 , , 
|
| Funzione di Rosenbrock
|
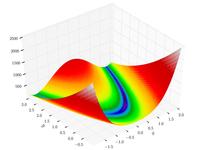
|
![{\displaystyle f({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(x_{i}-1\right)^{2}\right].\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/41f02e77049ab851fe048db982cf1e71246365e6)
|

|
 , , 
|
| Funzione di Powell[5]
|
|
 ![{\displaystyle \left.+(x_{4i-2}-2x_{4i-1})^{2}+(10x_{4i-3}-x_{4i})^{4}\right].\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1766a2b8383ab58acfcff1a3899ce2a8b57d2606)
|

|
![{\displaystyle x_{i}\in [-4,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7785901ee93fc41fb8e03cc673bd411cee1d85c5)

|
| Funzione di Beale
|

|


|

|

|
| Funzione di Goldstein–Price
|
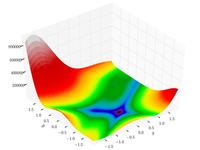
|


|

|

|
| Funzione di Booth
|
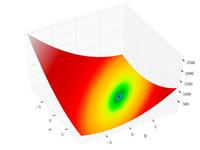
|

|

|
 . .
|
| Funzione di Bukin n.6
|
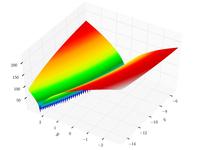
|

|

|
 , , 
|
| Funzione di Matyas
|
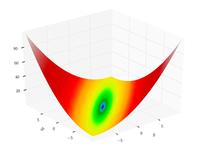
|

|

|

|
| Funzione di Lévi n.13
|
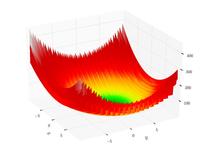
|


|

|

|
| Funzione del cammello a tre gobbe
|
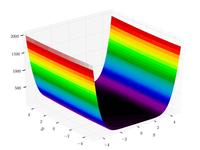
|

|

|

|
| Funzione di Easom
|
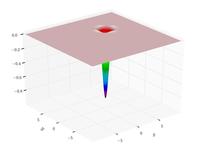
|

|

|

|
| Funzione cross-in-tray
|
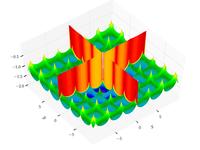
|

|

|

|
| Funzione di Eggholder
|
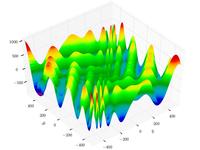
|

|

|

|
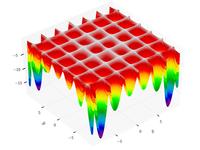
| Funzione di Hölder
|
|

|

|

|
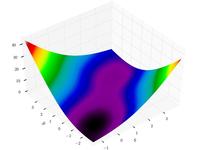
| Funzione di McCormick
|
|

|

|
 , , 
|
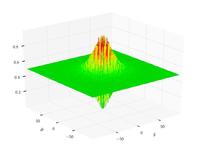
| Funzione di Schaffer N. 2
|
|

|

|

|
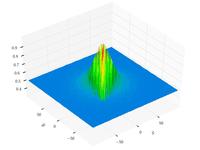
| Funzione di Schaffer N. 4
|
|

|

|

|
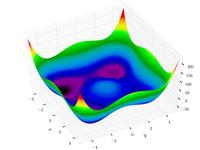
| Funzione di Styblinski–Tang
|
|

|

|
 , ,  . .
|
| Funzione di Simionescu[6]
|

|
 , ,


|

|

|
Funzioni test per problemi MOP
Le seguenti funzioni test per algoritmi di ottimizzazione multiobiettivo provengono da Deb,[7] Binh et. al.[8] e Binh.[9][10][11]
| Nome |
Fronte di Pareto |
Funzioni |
Vincoli |
Dominio di ricerca
|
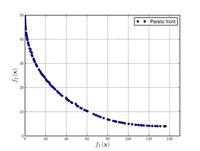
| Funzione di Binh e Korn
|
|

|

|
 , , 
|
| Funzione di Chakong e Haimes
|

|

|

|

|
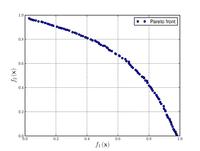
| Funzione di Fonseca e Fleming
|
|

|
|
 , , 
|
| Funzione test n. 4[9]
|
![Test function 4.[9]](//upload.wikimedia.org/wikipedia/commons/thumb/3/3c/Test_function_4_-_Binh.pdf/page1-200px-Test_function_4_-_Binh.pdf.jpg)
|

|

|

|
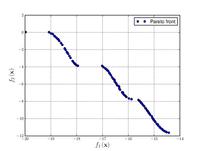
| Funzione di Kursawe
|
|
![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{2}\left[-10\exp \left(-0.2{\sqrt {x_{i}^{2}+x_{i+1}^{2}}}\right)\right]\\&\\f_{2}\left({\boldsymbol {x}}\right)&=\sum _{i=1}^{3}\left[\left|x_{i}\right|^{0.8}+5\sin \left(x_{i}^{3}\right)\right]\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a545df8c08a178973284eae8924aab67ce46077a)
|
|
 , ,  . .
|
| Funzione di Schaffer n. 1
|
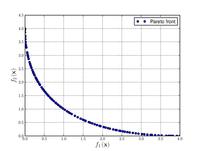
|

|
|
 . Values of . Values of  form form  to to  have been used successfully. Higher values of have been used successfully. Higher values of  increase the difficulty of the problem. increase the difficulty of the problem.
|
| Funzione di Schaffer n. 2
|

|

|
|
 . .
|
| Funzione di Poloni
|
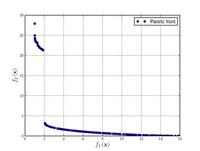
|
![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)&=\left[1+\left(A_{1}-B_{1}\left(x,y\right)\right)^{2}+\left(A_{2}-B_{2}\left(x,y\right)\right)^{2}\right]\\f_{2}\left(x,y\right)&=\left(x+3\right)^{2}+\left(y+1\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6b4a1275cbe615b285fbbcdb840a9a488360cc5)

|
|

|
| Funzione di Zitzler–Deb–Thiele n. 1
|

|

|
|
 , ,  . .
|
| Funzione di Zitzler–Deb–Thiele n. 2
|
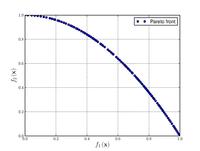
|

|
|
 , ,  . .
|
| Funzione di Zitzler–Deb–Thiele's function n. 3
|
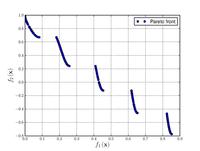
|

|
|
 , ,  . .
|
| Funzione di Zitzler–Deb–Thiele n. 4
|
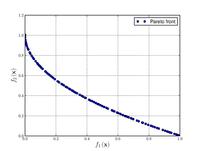
|

|
|
 , ,  , , 
|
| Funzione di Zitzler–Deb–Thiele n. 6
|

|
![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)&=1-\exp \left(-4x_{1}\right)\sin ^{6}\left(6\pi x_{1}\right)\\f_{2}\left({\boldsymbol {x}}\right)&=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)&=1+9\left[{\frac {\sum _{i=2}^{10}x_{i}}{9}}\right]^{0.25}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)&=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73a519e6f7ca429b41031cd0873fce161941b009)
|
|
 , ,  . .
|
| Funzione di Viennet
|
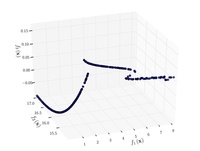
|

|
|
 . .
|
| Funzione di Osyczka e Kundu
|
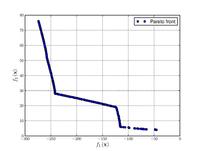
|

|

|
 , ,  , ,  . .
|
| Funzione CTP1[7]
|
![CTP1 function (2 variables).[7]](//upload.wikimedia.org/wikipedia/commons/thumb/d/d4/CTP1_function_%282_variables%29.pdf/page1-200px-CTP1_function_%282_variables%29.pdf.jpg)
|

|

|
 . .
|
| Problema Constr-Ex[7]
|
![Constr-Ex problem.[7]](//upload.wikimedia.org/wikipedia/commons/thumb/6/6f/Constr-Ex_problem.pdf/page1-200px-Constr-Ex_problem.pdf.jpg)
|

|

|
 , , 
|
Note
- ^ Neculai Andrei, An Unconstrained Optimization Test Functions Collection, in Advanced Modeling and Optimization, vol. 10, n. 1, 2008.
- ^ Thomas Bäck, Evolutionary algorithms in theory and practice: evolution strategies, evolutionary programming, genetic algorithms, Oxford, Oxford University Press, 1995, p. 328, ISBN 0-19-509971-0.
- ^ Randy L. Haupt e Sue Ellen, Practical genetic algorithms with DC-Rom, 2ª ed., New York, J. Wiley, 2004, ISBN 0-471-45565-2.
- ^ Rody Oldenhuis, Many test functions for global optimizers, su mathworks.com, Mathworks. URL consultato il 1º novembre 2012.
- ^ Sonja Surjanovich e Derek Bingham, Powell Function, su sfu.ca, Simon Fraser University. URL consultato il 21 maggio 2014 (archiviato il 21 maggio 2014).
- ^ P.A. Simionescu, Computer Aided Graphing and Simulation Tools for AutoCAD Users, 1st, Boca Raton, FL, CRC Press, 2014, ISBN 978-1-4822-5290-3.
- ^ a b c d e Deb, Kalyanmoy (2002) Multiobjective optimization using evolutionary algorithms (Repr. ed.). Chichester [u.a.]: Wiley. ISBN 0-471-87339-X.
- ^ Binh T. and Korn U. (1997) MOBES: A Multiobjective Evolution Strategy for Constrained Optimization Problems. In: Proceedings of the Third International Conference on Genetic Algorithms. Czech Republic. pp. 176-182
- ^ a b c Binh T. (1999) A multiobjective evolutionary algorithm. The study cases. Technical report. Institute for Automation and Communication. Barleben, Germany
- ^ Il software sviluppato da K. Deb è disponibile presso http://www.iitk.ac.in/kangal/codes.shtml Archiviato il 30 settembre 2014 in Internet Archive.
- ^ Gilberto A. Ortiz, Multi-objective optimization using ES as Evolutionary Algorithm., su mathworks.com, Mathworks. URL consultato il 1º novembre 2012.
Voci correlate
Altri progetti
|
|