Funzione càdlàg
|
Read other articles:

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

النمسا ملكية هابسبورغ Habsburgermonarchie ↓ 1526 – 1804 ملكية هابسبورغعلم ملكية هابسبورغشعار ملكية هابسبورغ في 1789. عاصمة فيينا(1526–1583)براغ(1583–1611)فيينا(1611–1804) نظام الحكم إقطاعية ملكية اللغة الرسمية الألمانية الديانة الديانة الرسمية:[بحاجة لمصدر]الكنيسة الرومانية الكاثو...
Bagian dari seri PolitikBentuk dasar dari pemerintahan Struktur kekuatan Konfederasi Federasi Hegemoni Kerajaan Negara kesatuan Sumber kekuatan Demokrasi Langsung Perwakilan Semi lainnya Kerajaan Mutlak Konstitusi Oligarki Aristokrasi Junta militer Kleptokrasi Plutokrasi Stratokrasi Timokrasi Otokrasi Otoritarianisme Despotisme Diktatur (Kediktatoran) Totalitarianisme Republik Parlementer Presidensial Semi presidensial Lainnya Anarki Anokrasi Khilafah Kritarsi Meritokrasi Oklokrasi Parti...

Ini adalah nama Korea; marganya adalah Jung. Jung Hae-inJung Hae-in pada tahun 2019Lahir1 April 1988 (umur 36)Seoul, Korea SelatanPendidikanUniversitas PyeongtaekPekerjaanAktorTahun aktif2013–sekarangAgenFNC EntertainmentTinggi178 cm (5 ft 10 in)[1]Nama KoreaHangul정해인 Hanja丁海寅 Alih AksaraJeong Hae-inMcCune–ReischauerChŏng Hae-in Jung Hae-in (lahir 1 April 1988) adalah seorang aktor Korea Selatan. Dia adalah penerima berbagai penghargaan di bid...

Medical conditions more common in autistic people This article needs to be updated. The reason given is: The article's text does not yet reflect that since DSM-5 (2013) and ICD-11 (2022) there is one unified Autism Spectrum Disorder diagnosis. Please help update this article to reflect recent events or newly available information. (July 2023) Autism spectrum disorders (ASD) are neurodevelopmental disorders that begin in early childhood, persist throughout adulthood, and affect three crucial a...

1167–1250 Italian anti-Imperial alliance For the political party, see Lega Lombarda. Member cities of the first and second Lombard League. The Lombard League (Liga Lombarda in Lombard, Lega Lombarda in Italian) was a medieval alliance formed in 1167,[1] supported by the popes, to counter the attempts by the Hohenstaufen Holy Roman emperors to assert influence over the Kingdom of Italy as a part of the Holy Roman Empire. At its apex, it included most of the cities of Northern Italy, ...

Andrus Ansip Andrus Ansip en 2017. Fonctions Député européen En fonction depuis le 2 juillet 2019(4 ans et 10 mois) Élection 26 mai 2019 Législature 9e Groupe politique RE 1er juillet – 31 octobre 2014(3 mois et 30 jours) Élection 25 mai 2014 Législature 8e Groupe politique ADLE Vice-président de la Commission européenneChargé du Marché numérique unique 1er novembre 2014 – 1er juillet 2019(4 ans et 8 mois) Président Jean-Claude Juncker Gouvernem...

American superhero comic This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. See Wikipedia's guide to writing better articles for suggestions. (August 2021) (Learn how and when to remove this message)Comics character Flaming Carrot ComicsThe Flaming Carrot, from Flaming Carrot #4 (Image Comics, 2006); art by Bob Burden.Publication informationPublisherAardvark-Vanaheim (1984–1985)Renegade Press (1985–1987)Dark Horse Comics (1988–2002)Image Comics (2004�...

1939 film by Roy Del Ruth For other uses of Tailspin, see Tailspin (disambiguation). Not to be confused with the Disney animated TV series TaleSpin. Tail SpinTheatrical film posterDirected byRoy Del RuthWritten byFrank WeadBased onWomen with Wings: A Novel of the Modern Day Aviatrix1935 novelby Genevieve HaugenProduced byDarryl F. ZanuckStarringAlice FayeConstance BennettNancy KellyJoan DavisCharles FarrellJane WymanCinematographyKarl FreundEdited byAllen McNeilMusic byLouis SilversProduction...

Audi R8 (Type 4S), an example of an M4 vehicle In automotive design, an M4, or Mid-engine, Four-wheel-drive layout places the internal combustion engine in the middle of the vehicle, between both axles and drives all four road wheels. It is a type of car powertrain layout. Although the term mid-engine can mean the engine is placed anywhere in the car such that the centre of gravity of the engine lies between the front and rear axles[citation needed], it is usually used for sports cars...

Forum of 19 countries along with EU and AU For other uses, see G20 (disambiguation). G20Group of TwentyAll leaders at the 2021 G20 Summit in Rome, Italy. Member countries of the G20 Countries represented through the membership of the European Union Countries represented through the membership of the African Union Countries permanently invited (Spain)Formation26 September 1999 (24 years ago) (1999-09-26)2008 (2008) (heads-of-sta...

American computer scientist Steven Sol SkienaBorn (1961-01-30) January 30, 1961 (age 63)NationalityAmericanAlma materUniversity of Illinois at Urbana-ChampaignScientific careerFieldsComputer scienceInstitutionsStony Brook University (1988–present)Doctoral advisorHerbert Edelsbrunner Steven Sol Skiena (born January 30, 1961) is a Computer Scientist and Distinguished Teaching Professor of Computer Science at Stony Brook University.[1] He is also Director of AI Institute at S...

Sojuz MS-24Dati della missioneNSSDC ID2023-143A SCN57862 VettoreSojuz 2.1a Lancio15 settembre 2023 15:44[1] Luogo lancioCosmodromo di Bajkonur Site 31 Atterraggio6 aprile 2024 07:17 UTC Parametri orbitaliOrbitaOrbita terrestre bassa Apoapsidekm Periapsidekm Inclinazione51.66° EquipaggioNumero3 MembriLoral O'Hara Solo lancioOleg KononenkoNikolaj Čub Solo atterraggioOleg NovickijMarina Vasilevskaja Da sx: O'Hara, Kononenko e Čub Programma SojuzMissione precedenteMissione successivaSo...

Özcan MelkemichelNazionalità Svezia Calcio RuoloAllenatore Squadra Syrianska Termine carriera1992 - giocatore CarrieraGiovanili 1978-1983 Syrianska Squadre di club1 1983-1992 Syrianska? (?) Carriera da allenatore 2003-2004 Syrianska2005-2013 Syrianska2014-2016 AFC United2017-2018 Djurgården2020-2021 AFC Eskilstuna2023- Syrianska 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un...

The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: St. Jakob Arena – news · newspapers · books · scholar · JSTOR (March 2024) ...

Genus of birds Ninox Morepork(Ninox novaeseelandiae) Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Strigiformes Family: Strigidae Genus: NinoxHodgson, 1837 Type species Ninox nipalensis[1] = Strix lugubrisTickell 1833 Ninox is a genus of true owls comprising 36 species found in Asia and Australasia. Many species are known as hawk-owls or boobooks, but the northern hawk-owl (Surnia ulula) is not a member of this genus. Taxonomy The ge...

Military unit of the Indian Army Men of the 2nd Battalion, 5th Gorkha Rifles (Frontier Force) of the Indian Army operating alongside soldiers from the 82nd Airborne Division of the US Army in 2013 At the time of Indian Independence in 1947, as per the terms of the Britain–India–Nepal Tripartite Agreement, six Gorkha regiments, formerly part of the British Indian Army, became part of the Indian Army and have served ever since. The troops are mainly from ethnic Gurkha communities of Nepal. ...

Cet article est une ébauche concernant une localité malgache. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Antsoha Administration Pays Madagascar Région Ihorombe Province Fianarantsoa District Ihosy Démographie Population 4 676 hab.[1] (2018) Géographie Coordonnées 21° 53′ 24″ sud, 46° 08′ 02″ est Localisation Géolocalisation sur la carte : Madagas...
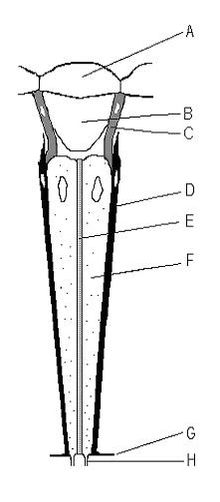
Omatidia pada udang geragau berbentuk segi enam Omatidium:A – korneaB – kerucut kristalinC & D – sel pigmenE – rhabdomF – sel-sel fotoreseptorG – membrana fenestrataH – saraf optik Omatidium (jamak: omatidia) merupakan masing-masing reseptor penglihatan mata majemuk pada artropoda seperti serangga, krustasea dan kaki seribu. Omatidia berfungsi secara terpisah sebagai reseptor warna,[1] menyediakan informasi penglihatan kepada otak dengan gambar masing-masing. Seluruh...

ポール・ジョージPaul George インディアナ・ペイサーズでのジョージ(2014年)フィラデルフィア・76ers No.8ポジション SG / SF所属リーグ NBA基本情報愛称 PG13Playoff P国籍 アメリカ合衆国生年月日 (1990-05-02) 1990年5月2日(34歳)出身地 カリフォルニア州パームデール身長 203cm (6 ft 8 in)体重 100kg (220 lb)ウィングスパン 211cm (6 ft 11 in)[1 ...




![{\displaystyle [0,T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35ccef2d3dc751e081375d51c111709d8a1d7ac6)
























