Dilemma del prigioniero
|
Read other articles:

Koordinat: 54°19′43″N 2°44′42″W / 54.32861°N 2.74500°W / 54.32861; -2.74500 Pemandangan Kendal Untuk tempat lain yang bernama sama, lihat Kendal (disambiguasi). Kendal adalah sebuah kota di Cumbria, Inggris. Terletak 64 km di selatan Carlisle, di Sungai Kent, penduduknya mencapai 27.521 jiwa. Dahulu Kendal adalah bagian dari Westmorland. Karena bangunan-bangunan yang dibangun dari batu kapur, kota ini dijuluki 'Auld Grey Town. Sejarah Disebutkan di Dom...

Poltava (Ukrainian: Полта́ваcode: uk is deprecated ) ialah kota dan pusat oblast di Provinsi Poltava di Ukraina tengah dengan sejumlah 313.400 penduduk (2004). Iklim Data iklim Poltava (1980-2018) Bulan Jan Feb Mar Apr Mei Jun Jul Agt Sep Okt Nov Des Tahun Rekor tertinggi °C (°F) 9.4 (48.9) 16.0 (60.8) 22.4 (72.3) 29.9 (85.8) 34.2 (93.6) 35.7 (96.3) 37.2 (99) 39.4 (102.9) 33.5 (92.3) 29.6 (85.3) 19.3 (66.7) 13.5 (56.3) 39.4 (102.9) Rata-rata tertinggi °C (°F) −2.0 (28.4) −1.1 ...

Pekerja lingkungan meletakkan containment boom di kawasan Pangkalan Angkatan Udara Offutt ketika banjir untuk mengantisipasi kemungkinan menyebarnya bahan bakar yang bocor ke lingkungan Ekologi terapan adalah salah satu sub-bidang ekologi yang menggunakan ilmu terapan dari ilmu ekologi untuk menyelesaikan permasalahan di dunia. Ekologi terapan juga mencakup bidang ilmu yang fokus kepada penerapan konsep, teori, model, atau metode-metode ekologi dasar ke permasalahan lingkungan.[1] Kon...

Queen of Jordan since 1999 RaniaThe Queen in 2018Queen of JordanTenure7 February 1999 – presentProclamation22 March 1999PredecessorQueen NoorBornRania Al-Yassin (1970-08-31) 31 August 1970 (age 53)Kuwait City, KuwaitSpouse Abdullah II of Jordan (m. 1993)Issue Hussein, Crown Prince of Jordan Princess Iman Princess Salma Prince Hashem Regnal nameRania Al AbdullahFatherFaisal Al-YassinMotherIlham YassinSignature Rania Al Abdullah[1] (Arabic: ...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (décembre 2018). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes. Cet article est une ébauche concernant l’hist...

American college basketball season 1909–10 Illinois Fighting Illini men's basketballConferenceBig Ten ConferenceRecord5–4 (5–4 Big Ten)Head coachHerb V. JuulCaptainCarl WatsonHome arenaKenney GymSeasons← 1908–091910–11 → 1909–10 Western Conference men's basketball standings vte Conf Overall Team W L PCT W L PCT Chicago 9 – 3 .750 10 – 3 .769 Minnesota 7 – 3 .700 10 – 3 ....

LDS Church temple in Le Chesnay, Paris, France Paris France TempleNumber156Dedication21 May 2017, by Henry B. EyringSite2.26 acres (0.91 ha)Floor area44,175 sq ft (4,104.0 m2)Official website • News & imagesChurch chronology ←Hartford Connecticut Temple Paris France Temple →Tucson Arizona Temple Additional informationAnnounced15 July 2011, by Thomas S. MonsonGroundbreakingNo formal groundbreaking[1]Open house22 April - 13 May 2017Current presidentDomi...

British Egyptologist (1853–1942) SirFlinders PetrieFRS FBAPetrie in 1903BornWilliam Matthew Flinders Petrie(1853-06-03)3 June 1853Charlton, London, United KingdomDied28 July 1942(1942-07-28) (aged 89)Jerusalem, Mandatory PalestineResting placeMount Zion CemeteryKnown forProto-Sinaitic script, Merneptah Stele, pottery seriation[2]Spouse Hilda Urlin (m. 1896)Awards Fellow of the Royal Society[1] Huxley Memorial Medal (1906) Scientific c...

Lisa Gaye con Richard Boone in una foto pubblicitaria per la serie televisiva Have Gun - Will Travel Lisa Gaye, nata Lesli Griffin[1] (Denver, 6 marzo 1935 – Houston, 14 luglio 2016[2]), è stata un'attrice statunitense. Era figlia del pittore Frank Henry Griffin[3] e dell'attrice Margaret Allen (nata Gibson)[4] e sorella delle attrici Teala Loring e Debra Paget e del truccatore e attore Frank Griffin.[5] Ha recitato in 14 film dal 1954 al 1967 ed è ...

Roman Catholic military order founded by crusaders around 1119 This article is about the medieval Catholic military order. For its successor, see Order of Saints Maurice and Lazarus. For other uses, see Order of Saint Lazarus (disambiguation). For the society of apostolic life also known as Lazarists, see Congregation of the Mission. Order of Saint Lazarus of JerusalemFlag of the orderSuccessorOrder of Saints Maurice and Lazarus (Italian branch, since 1572)Order of Our Lady of Mount Carmel an...
Ikon Transfigurasi oleh Feofan Grek, abad ke-15 Perayaan Transfigurasi Yesus (dikenal juga sebagai Pesta Yesus menampakkan Kemuliaan-Nya) dirayakan oleh berbagai denominasi Kristen. Asal usul perayaan mungkin berasal dari dedikasi tiga basilika di Gunung Tabor.[1] Perayaan ini hadir dalam berbagai bentuk sejak abad ke-9, dan di Gereja Barat dibuat universal 6 Agustus oleh Paus Kallistus III untuk memperingati Pengepungan Belgrade (1456).[2] Di Ortodoks Suriah, Ortodoks India, ...

Tibetan teacher Yongey Mingyur RinpocheMingyur Rinpoche in 2016TitleRinpochePersonalBorn1975NepalReligionKagyu Nyingma Part of a series onTibetan Buddhism Schools Nyingma Kadam Sakya Bodong Kagyu Jonang Gelug Rimé Key personalities First dissemination Padmasambhāva Śāntarakṣita Kamalaśīla Songtsen Gampo Trisong Detsen Ralpacan Second dissemination Atiśa Talika Abhayakirti Niguma Sukhasiddhi Milarepa Nyingma Yeshe Tsogyal Longchenpa Jigme Lingpa Patrul Rinpoche Dudjom Lingpa Mipham Ka...

تشكل الحياة السياسية في إنجلترا الجزء الأكبر من الحياة السياسية الأوسع نطاقًا للمملكة المتحدة، باعتبار إنجلترا أكثر اكتظاظًا بالسكان من جميع البلدان الأخرى في المملكة المتحدة مجتمعة. ونظرًا لأن إنجلترا أيضًا هي الأكبر من حيث المساحة والناتج المحلي الإجمالي، فإن علاقته�...
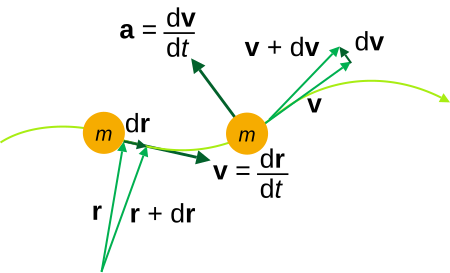
「位置」の語義については、ウィクショナリーの「位置」の項目をご覧ください。 位置(いち、英語: position)とは、物体が空間の中のどこにあるかを表す物理量である。 概要 原点Oから物体の位置Pへのベクトル(位置ベクトル (position vector))で表される。 通常は x, r, s で表され、O から P までの各軸に沿った直線距離に対応する[1]。 r = O P → {\displaystyle \...

Extinct Italic language VestinianCountry of the Vestini looking from Pescara to Gran SassoRegionEast-central ItalyEraca. 250–100 BC[1]Language familyIndo-European ItalicOsco-Umbrian?Oscan?VestinianLanguage codesISO 639-3xvsLinguist ListxvsGlottologvest1239 Vestinian is an extinct Italic language documented only in two surviving inscriptions of the Roman Republic. It is presumed to have been anciently spoken by the tribe of the Vestini, who occupied the region within current Abruzzo ...

ArienzoKomuneComune di ArienzoLokasi Arienzo di Provinsi CasertaNegaraItaliaWilayah CampaniaProvinsiCaserta (CE)Luas[1] • Total14,01 km2 (5,41 sq mi)Ketinggian[2]70 m (230 ft)Populasi (2016)[3] • Total5.333 • Kepadatan380/km2 (990/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos81021Kode area telepon0823Situs webhttp://www.comune.arienzo.ce.it Arienzo adala...

Artur Barciś Artur Barciś (IPA: [ˈartur ˈbarʲʨ̑ĩɕ]) (Kokawa, 12 agosto 1956) è un attore polacco, noto soprattutto per aver interpretato il ruolo del testimone silenzioso nel Decalogo del regista Krzysztof Kieślowski. Filmografia parziale L'uomo di ferro, regia di Andrzej Wajda, 1981 Senza fine, regia di Krzysztof Kieślowski, 1985 Decalogo 1, regia di Krzysztof Kieślowski, 1989 Decalogo 2, regia di Krzysztof Kieślowski, 1990 Decalogo 3, regia di Krzysztof Kieślowski, 1990 Decal...

Provinsi Xorazm Xorazm viloyati Region Negara Uzbekistan Ibukota Urgench Area 6.300 km2 (2.432 sq mi) Population 1.200.000 (2005) Density 190 / km² (492 / sq mi) ISO 3166-2 UZ-XO Website: Situs web resmi Provinsi Xorazm (bahasa Uzbek: Xorazm viloyati, Хоразм вилояти) atau Provinsi Khorezm adalah sebuah provinsi Uzbekistan yang memiliki luas wilayah 6.300 km² dan memiliki populasi 1.200.000 jiwa (2005). Ibu kotanya ialah Urgench. Distrik Pr...

クリスティアン・モルゲンシュテルンChristian Morgenstern Friedrich Dürckによる肖像画誕生日 1805年9月29日出生地 ローマ=ドイツ帝国 自由ハンザ都市ハンブルク死没年 1867年2月16日死没地 バイエルン王国、ミュンヘンテンプレートを表示 クリスティアン・モルゲンシュテルン(Christian Ernst Bernhard Morgenstern、1805年9月29日 - 1867年2月16日)はドイツの風景画家である。 略歴 ハンブ...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 野村秀雄 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2015年5月) 野村 秀雄(のむら ひでお、1888年1月8日 - 1964年6月...












