Azione di Nambu-Goto
|
Read other articles:

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Love Ayumi Hamasaki EP – news · newspapers · books · scholar · JSTOR (May 2023) (Learn how and when to remove this template message) 2012 EP by Ayumi HamasakiLoveEP by Ayumi HamasakiReleasedNovember 8, 2012 (2012-11-08)Recorded2012Ge...

Zamperini pada Mei 2014 Louis Silvie Zamperini (26 Januari 1917 – 2 Juli 2014) adalah seorang korban selamat tahanan perang AS dalam Perang Dunia II, penginjil Kristen dan pelari jarak jauh Olimpiade. Zamperini adalah subyek dari dua film biografi, film tahun 2014 Unbroken dan film tahun 2015 Captured by Grace. Referensi Catatan Kutipan Daftar pustaka Hillenbrand, Laura. Unbroken: A World War II Story of Survival, Resilience, and Redemption. New York: Random House, 2010. ISBN ...

Pour les articles homonymes, voir Arbon. Arbon L’église Saint-Martin et château vus du port en 2006. Armoiries Logo Administration Pays Suisse Canton Thurgovie District Arbon NPA 9320 No OFS 4401 Démographie Populationpermanente 15 459 hab. (31 décembre 2022) Densité 2 603 hab./km2 Langue Allemand Géographie Coordonnées 47° 31′ 00″ nord, 9° 26′ 00″ est Altitude 399 m Superficie 5,94 km2 Localisation Carte de ...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

KTM ETSKTM Electric Train ServiceKereta KTM Kelas 93 (Layanan Platinum) tiba di KamparIkhtisarNama asliPerkhidmatan Tren Elektrik (Melayu)电动列车服务 (Tionghoa)மின்சார ரயில் சேவை (Tamil)JenisKereta antarkotaKereta semi cepatLokasiPadang Besar - Butterworth - Ipoh - Kuala Lumpur - Gemas - (Johor Bahru pada pertengahan 2025)Stasiun36 (per 15 Januari 2022)[2]Penumpang harian10.489 (Kuartal ketiga 2018)[1]Penumpang3,902 juta (2019)Situs webww...
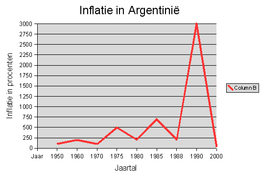
Hiperinflasi di Argentina Hiperinflasi, dalam ilmu ekonomi, adalah inflasi yang tidak terkendali, kondisi ketika harga-harga naik begitu cepat dan nilai uang menurun drastis dan diluar kendali yang terjadi dalam perekonomian suatu negara. Secara formal, hiperinflasi terjadi jika tingkat inflasi lebih dari 50% dalam satu bulan.[1] Sebagai sebuah aturan ibu jari, inflasi biasanya dilaporkan setahun sekali, tetapi dalam kondisi hiperinflasi, tingkat inflasi dilaporkan dalam interval yang...
County in Kansas, United States This article is about Shawnee County, Kansas. For the city in Johnson County, see Shawnee, Kansas. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Shawnee County, Kansas – news · newspapers · books · scholar · JSTOR (January 2012) (Learn how and when to remove this message) Co...

ThothThoth, dalam salah satu perwujudannya sebagai manusia berkepala burung ibisDewa Ilmu Pengetahuan dan TulisanPusat pemujaanHermopolisSimbolcakram bulan, gulungan papyrusOrangtuaTidak ada (menciptakan dirinya sendiri); alternatif Ra atau Horus dan Hathor,PasanganSeshat, Ma'at, Bastet atau Hathor Thoth (diucapkan / θoʊθ / atau / toʊt /) adalah salah satu dewa paling penting di peradaban Mesir Kuno. Ia dianggap sebagai dewa penulisan, dewa kebajikan, dewa pembawa mukjizat, dan dewa bulan...

Alex Brosque Informasi pribadiNama lengkap Alex BrosqueTanggal lahir 12 Oktober 1983 (umur 40)Tempat lahir Sydney, New South Wales, AustraliaTinggi 1,81 m (5 ft 11+1⁄2 in)Posisi bermain Penyerang, sayap kiri, gelandang tengahInformasi klubKlub saat ini Al AinNomor 32Karier junior2001 AISKarier senior*Tahun Tim Tampil (Gol)2001–2004 Marconi Stallions 53 (13)2004–2005 Feyenoord 0 (0)2004–2005 → Westerlo (pinjaman) 16 (2)2005–2006 Brisbane Roar 21 (8)2006–2...

List of water polo players Main article: Water polo at the 1984 Summer Olympics The following are complete rosters for the twelve men's water polo teams that competed in the 1984 Summer Olympics water polo tournament played in August 1984. Each team registered 13 players which are ordered by their respective team numbers. Players marked with † were unused throughout the tournament. Names of coaches are taken from the official Olympics report. Player ages are correct as of 1 August 1984, th...

1931 film This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kiki 1931 film – news · newspapers · books · scholar · JSTOR (February 2015) (Learn how and when to remove this message) KikiTheatrical release posterDirected bySam TaylorWritten byPlay:David Belasco André Picard Screenplay:Sam TaylorProduced by...

Pour les articles homonymes, voir Hollerich (homonymie). Cet article est une ébauche concernant une localité luxembourgeoise. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Hollerich (lb) Hollerech Immeubles de bureaux et passerelle sur la Pétrusse Administration Pays Luxembourg Canton Luxembourg Commune Luxembourg Statut Ancienne commune (avant 1920) Démographie Population 7 834 hab.[1] (31 déce...

Cet article est une ébauche concernant le cyclisme. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Chateau d'AxInformationsStatut Équipe proDiscipline Cyclisme sur routePays ItalieCréation 1983Disparition 1993Saisons 11Dénominations1983 Mareno-Wilier Triestina1984-1985 Supermercati Brianzoli1986 Supermercati Brianzoli-Essebi1987 Supermercati Brianzoli-Chateau d'Ax1988-1990 Chateau d'Ax-Salotti1991-199...

Markers identifying overhead lines to aircraft Overhead wire markers are safety instruments applied to the overhead power lines marking transmission lines and ropeways along the flight path during the day.[1][2] markers on a line near an airfield Markers are often installed on overhead lines near airfields, or at river crossings where there is a possibility of float-equipped aircraft using the river. Some markers contain conductor marking lights or strobe lights to improve vis...

Cet article est une ébauche concernant une unité ou formation militaire et le Nigeria. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Forces armées nigérianesNigerian Armed Forces Drapeau des Forces armées nigérianes Fondation 1900 (Force frontalière royale ouest-africaine) Branches ArméeForce aérienneMarine Commandement Président Hachim MAHAMAT Ministre de la Défense Mansur Muhammed Dan - Ali Main-d...
هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. المطلقية الأخلاقية هي رأي أخلاقي مفاده أن جميع الأعمال صحيحة أو خاطئة في جوهرها. على سبيل المثال، قد يُعتبر السرقة غير أخلاقي دائمًا، حتى لو تم ذلك من أجل رفاهية الآخرين (على �...

Village in Northeast Constituency, IcelandStöðvarfjörðurVillageAerial viewLocation of the Municipality of FjarðabyggðStöðvarfjörðurLocation in IcelandCoordinates: 64°50′00″N 13°52′27.6″W / 64.83333°N 13.874333°W / 64.83333; -13.874333Country IcelandConstituencyNortheast ConstituencyRegionEastern RegionMunicipality FjarðabyggðPopulation (2018) • Total184Time zoneUTC+0 (GMT)WebsiteOfficial website Stöðvarfjörður (Icelandi...

لمعانٍ أخرى، طالع موريس (توضيح). موريس الإحداثيات 42°57′58″N 96°10′51″W / 42.966111111111°N 96.180833333333°W / 42.966111111111; -96.180833333333 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة سايو خصائص جغرافية المساحة 1.574642 كيلومتر مربع1.435653 كي�...

Hank PfisterNazionalità Stati Uniti Altezza193 cm Peso84 kg Tennis Termine carriera1988 Carriera Singolare1 Vittorie/sconfitte 260-212 Titoli vinti 2 Miglior ranking 19º (2 maggio 1983) Risultati nei tornei del Grande Slam Australian Open SF (1978, 1981, 1982) Roland Garros 2T (1978) Wimbledon 4T (1978, 1980, 1982) US Open 3T (1979, 1980) Doppio1 Vittorie/sconfitte 277-217 Titoli vinti 11 Miglior ranking 12º (13 dicembre 1982) Risultati nei tornei del Grande Sl...

Fictional character on Desperate Housewives Soap opera character Lynette ScavoDesperate Housewives characterPortrayed byFelicity HuffmanDuration2004–2012First appearancePilot1x01, October 3, 2004Last appearanceFinishing the Hat8x23, May 13, 2012Created byMarc CherrySpin-offappearancesDesperate Housewives: The Game (2006)In-universe informationOther namesLynette Lindquist (maiden name)Lynnie (by her mother)OccupationCEO[1]FormerInterior designerRestaurant ManagerV...































