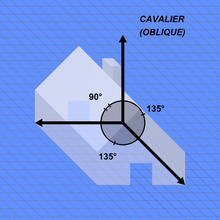
Assonometria
|
Read other articles:

Archaeognatha Petrobius maritimus (en) TaksonomiKerajaanAnimaliaFilumArthropodaKelasInsectaOrdoArchaeognatha Börner, 1904 Tata namaSinonim taksonMicrocoryphia (en) lbs Archaeognatha adalah ordo primitif dari serangga. Nama Archeognatha berasal dari bahasa Yunani, archaios yang berarti primitif dan gnathos yang berarti rahang. Ordo serangga ini rata-rata panjangnya 10-12mm merupakan ordo serangga tak bersayap. Serangga berbentuk silindris ini juga tidak bermetamorfosis, hanya berganti kulit s...

SidomulyoKelurahanGapura selamat datang di Kelurahan SidomulyoNegara IndonesiaProvinsiSumatera UtaraKotaMedanKecamatanMedan TuntunganKodepos20137Kode Kemendagri12.71.07.1006 Kode BPS1275010002 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Untuk kegunaan lain, lihat Sidomulyo. Sidomulyo adalah kelurahan di kecamatan Medan Tuntungan, Medan, Sumatera Utara, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhi...

Sudaporn SeesondeeInformasi pribadiLahir4 Oktober 1991 (umur 32)Distrik Chai Wan, Provinsi Udon Thani, Thailand[1] OlahragaNegaraThailandOlahragaTinju Rekam medali Tinju amatir putri Mewakili Thailand Permainan Olimpiade 2020 Tokyo Kelas ringan Kejuaraan Dunia 2018 New Delhi Kelas ringan 2014 Kota Jeju Kelas welter ringan Pesta Olahraga Asia 2018 Jakarta Kelas ringan Sudaporn Seesondee (Thai: สุดาพร สีสอนดีcode: th is deprecated , lahir 4 Oktober 1...

American election 1948 Texas gubernatorial election ← 1946 November 2, 1948 1950 → Nominee Beauford H. Jester Alvin H. Lane Party Democratic Republican Popular vote 1,024,160 177,399 Percentage 84.72% 14.67% County resultsJester: 60–70% 70–80% 80–90% >90%Lane: 50–60% Governor before election Beauford ...

South African middle-distance runner Caster SemenyaOIBCaster Semenya in 2018Personal informationNationalitySouth AfricanBorn (1991-01-07) 7 January 1991 (age 33)Pietersburg, South AfricaAlma materNorth-West UniversityHeight1.78 m (5 ft 10 in)Weight70 kg (154 lb)Association football careerSenior career*Years Team Apps (Gls)2019–present JVW F.C. *Club domestic league appearances and goalsSportSportRunningEvent(s)800 metres, 1500 metresAchievements and titles...

العلاقات السورية الكوستاريكية سوريا كوستاريكا سوريا كوستاريكا تعديل مصدري - تعديل العلاقات السورية الكوستاريكية هي العلاقات الثنائية التي تجمع بين سوريا وكوستاريكا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ...

Gambar halaman pertama Beowulf, sebuah teks dalam bahasa Inggris Kuno. Sejarah bahasa Inggris bermula dari migrasi Anglo-Saxon ke pulau Britania pada sekitar 1.500 tahun yang lalu. Bahasa Inggris adalah sebuah bahasa Jermanik Barat yang berasal dari dialek-dialek Anglo-Frisia yang dibawa ke pulau Britania oleh para imigran Jermanik dari beberapa bagian barat laut daerah yang sekarang disebut Belanda dan Jerman. Pada awalnya, bahasa Inggris Kuno adalah sekelompok dialek yang mencerminkan asal ...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) فريدريك لوتز (بالألمانية: Friedrich A. Lutz) معلومات شخصية الميلاد 29 ديسمبر 1901 [1] الوفاة 4 أكتوبر 1975 (73 سنة) [1] زيورخ مواطنة ألمانيا عضو في جم�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bridgton Academy – news · newspapers · books · scholar · JSTOR (March 2023) (Learn how and when to remove this template message) School in North Bridgton, Maine, United StatesBridgton AcademyBridgton Academy's SealLocationNorth Bridgton, Maine 04057United State...
1980 American documentary film The Day After TrinityDVD cover, 2002, with photograph by Philippe Halsman, 1958Directed byJon H. ElseWritten byDavid PeoplesJanet PeoplesJon ElseProduced byJon H. Else[1]Peter Baker(executive producer)StarringHans BetheRobert SerberRobert WilsonFrank OppenheimerI.I. RabiFreeman DysonStanislaw UlamJ. Robert Oppenheimer (archive footage)Narrated byPaul FreesCinematographyTom McDonoughDavid EsparStephen LighthillEdited byDavid PeoplesRalph WikkeMusic byMart...

Extinct genus of dinosaurs MicroraptorTemporal range: Early Cretaceous, 120 Ma PreꞒ Ꞓ O S D C P T J K Pg N ↓ Fossil specimen, with white arrows pointing at preserved feathers Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Clade: Dinosauria Clade: Saurischia Clade: Theropoda Family: †Dromaeosauridae Clade: †Microraptoria Genus: †MicroraptorXu et al., 2000 Type species †Microraptor zhaoianusXu et al., 2000 Other species †M. gui Xu et al.,...

Mohammad Al Shalhoub Informasi pribadiNama lengkap Mohammad Bander Al-ShalhoubTanggal lahir 8 Desember 1980 (umur 43)Tempat lahir Riyadh, Arab SaudiTinggi 1,64 m (5 ft 5 in)Posisi bermain GelandangInformasi klubKlub saat ini Al-HilalNomor 10Karier senior*Tahun Tim Tampil (Gol)1998– Al-Hilal 304 (61)Tim nasional2000–2012 Arab Saudi 117 (19) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik dan akurat per 3 January 2012 Mohammad Al-Shalhoub (lah...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Casablanca Fan Company – news · newspapers · books · scholar · JSTOR (August 2019) (Learn how and when to remove this message) Casablanca Fan CompanyTraded asNYSE: CABFounded1974; 50 years ago (1974)[1]FounderBurton A. BurtonFatePurcha...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

الهاية دنهاخ، الهاي، لاهاي علم شعار الشعار:(بالهولندية: Vrede en Recht) الإحداثيات 52°05′N 4°19′E / 52.08°N 4.31°E / 52.08; 4.31 [1] تاريخ التأسيس القرن 13 تقسيم إداري البلد هولندا (9 يونيو 1815–)[2][3] التقسيم الأعلى جنوب هولندا (1840–)[4] ...

Australian politician (1845–1918) For other people named George Reid, see George Reid (disambiguation). The Right HonourableSir George ReidGCB GCMG KCReid in 19154th Prime Minister of AustraliaIn office18 August 1904 – 5 July 1905MonarchEdward VIIGovernor‑GeneralLord NorthcotePreceded byChris WatsonSucceeded byAlfred Deakin1st Leader of the OppositionIn office19 May 1901 – 17 August 1904Prime MinisterEdmund BartonAlfred DeakinChris WatsonPreceded byNew p...

1981 Canadian filmGasDirected byLes RoseWritten bySusan ScrantonDick WolfProduced byClaude HérouxStarringSusan AnspachHowie MandelSterling HaydenHelen ShaverPeter AykroydSandee CurrieKeith KnightDonald SutherlandCinematographyRené VerzierEdited byPatrick DoddMusic byPaul ZazaProductioncompaniesFilmplan InternationalDavis-Panzer ProductionsCanadian Film Development CorporationDistributed byParamount PicturesRelease date July 24, 1981 (1981-07-24) Running time94 minutesCountryC...

Gerbang Istana Hampton Court Palace. Marked A on the plan below.'1' Istana Hampton Court adalah sebuah istana Kerajaan Britania Raya yang berlokasi di borough London Richmond upon Thames, London Raya dan di county bersejarah Middlesex. Istana ini terletak 11,7 mil (18,8 kilometer) di sebelah selatan Charing Cross dan mulai dihuni oleh Keluarga Kerajaan Britania Raya pada abad ke-18. Hampton Court pada awalnya dibangun untuk Kardinal Thomas Wolsey, favorit Raja Henry VIII, sekitar tahun 1514. ...

Questa voce o sezione sull'argomento società calcistiche israeliane non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Questa voce sull'argomento società calcistiche israeliane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Beitar Tel Aviv Bat YamCalcio Segni distintiviUniformi di gara Casa Trasferta Colori social...