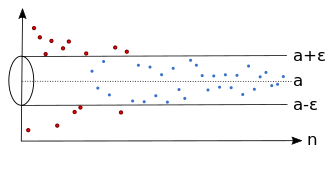
Limit barisan
| |||||||||||||||
Read other articles:

Air Terjun Terinting Lokasi di Indonesia Informasi Lokasi Desa Sempatung Lawek, Kecamatan Air Besar, Kabupaten Landak, Provinsi Kalimantan Barat, Indonesia. Negara Indonesia Koordinat 0°49′23″N 110°03′11″E / 0.823152°N 110.053097°E / 0.823152; 110.053097Koordinat: 0°49′23″N 110°03′11″E / 0.823152°N 110.053097°E / 0.823152; 110.053097 Air Terjun Terinting atau Air Terjun Rambo Terinting adalah sebuah air terjun yang...

Isotomus Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Coleoptera Famili: Cerambycidae Genus: Isotomus Isotomus adalah genus kumbang tanduk panjang yang berasal dari famili Cerambycidae. Genus ini juga merupakan bagian dari ordo Coleoptera, kelas Insecta, filum Arthropoda, dan kingdom Animalia. Larva kumbang dalam genus ini biasanya mengebor ke dalam kayu dan dapat menyebabkan kerusakan pada batang kayu hidup atau kayu yang telah ditebang. Referensi TITAN: Cera...

Sebuah lukisan tahun 1684 yang menggambarkan Vitruvius (kanan) menyajikan De Architectura untuk Kaisar Augustus Marcus Vitruvius Pollio (lahir 80-70 SM, meninggal setelah 15 SM), umumnya dikenal sebagai Vitruvius atau Vitruvi atau Vitruvio, seorang penulis, arsitek, insinyur sipil dan insinyur militer Romawi selama abad ke-1 SM, yang dikenal karena naskah multi-volumenya yang berjudul De architectura. Dalam keterangannya sendiri,[1] Vitruvius menjabat sebagai prajurit artileri, kelas ...

قضاء الرميثة قضاء الرميثة ونواحيه في محافظة المثنى تقسيم إداري البلد العراق [1] التقسيم الأعلى محافظة المثنى إحداثيات 31°29′52″N 45°17′44″E / 31.49777°N 45.29542°E / 31.49777; 45.29542 الرمز الجغرافي 9166568 تعديل مصدري - تعديل قضاء الرميثة هو أحد الأقضية العراقية ...

1989 Indian filmCarnivelDirected byP. G. ViswambharanWritten byS. N. SwamyProduced byShyney FilmsStarringMammoottyParvathySukumaranBabu AntonyCinematographyJ. WilliamsEdited byK. SankunniMusic byShyamProductioncompanyShyney FilmsDistributed byShyney FilmsRelease date 27 July 1989 (1989-07-27) CountryIndiaLanguageMalayalam Carnivel is a 1989 Malayalam comedy film written by S. N. Swamy and directed by P. G. Viswambharan. The film centres on the backdrops of a carnival. It stars...

Osservatorio di JenaL'osservatorio universitario di Jena e, sullo sfondo l'osservatorio pubblico Urania JenaCodice032 Stato Germania LocalitàJena Coordinate50°55′30.97″N 11°34′57.97″E / 50.92527°N 11.58277°E50.92527; 11.58277Coordinate: 50°55′30.97″N 11°34′57.97″E / 50.92527°N 11.58277°E50.92527; 11.58277 Altitudine143 m s.l.m. Climacontinentale Fondazione~ 1820 Sitowww.astro.uni-jena.de/index.php/home.html Mappa di localizzaz...

CesenaKomuneComune di CesenaPanorama of CesenaNegaraItaliaWilayahEmilia-RomagnaProvinsiForlì-Cesena (FC)Frazionilihat daftarPemerintahan • Wali kotaPaolo Lucchi (Democratic Party (Italy))Luas • Total249,47 km2 (9,632 sq mi)Ketinggian44 m (144 ft)Populasi (12-21-2009) • Total95.909 • Kepadatan3,8/km2 (10,0/sq mi)DemonimCesenatiZona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos47023Kode ar...

Ukrainian football club Dnipro Dnipropetrovsk redirects here. For other uses, see Dnipro Dnipropetrovsk (disambiguation). Not to be confused with SC Dnipro-1. Football clubDniproFull nameФутбо́льний Клуб «Дніпро́»Football Club DniproNickname(s)кораблі (The ships)Founded1918; 106 years ago (1918)Dissolved2019[1]GroundDnipro-Arena, DniproCapacity33,993OwnerIhor KolomoyskyiPresidentIhor KolomoyskyiLatest managerOleksandr Poklonskyi[2&#...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Vegetarianism and wine – news · newspapers · books · scholar · JSTOR (September 2014) (Learn how and when ...

Promethocene Names Other names Promethium cyclopentadienide Identifiers CAS Number 112341-23-8 Y 3D model (JSmol) Interactive image SMILES c1ccc[cH-]1.c2ccc[cH-]2.c3ccc[cH-]3.[Pm+3] Properties Chemical formula Pm(C5H5)3 Molar mass 340.285 Appearance yellow-orange solid[1] Boiling point 145~260 °C(10-3~10-4mmHg, sublimates) Related compounds Related compounds cyclopentadiene Except where otherwise noted, data are given for materials in their standard stat...

Natale in casa CupielloCommedia in tre atti Una scena della versione televisiva del 1977 AutoreEduardo De Filippo Lingua originalenapoletano, italiano GenereTeatro napoletano Composto nel1931 Prima assoluta25 dicembre 1931Kursaal di Napoli Personaggi Luca Cupiello Concetta, sua moglie Tommasino, loro figlio, detto Nennillo Ninuccia, la figlia Nicola, suo marito Pasqualino, fratello di Luca Raffaele, portiere Vittorio Elia Il dottore Carmela Olga Pastorelli Luigi Pastorelli Alberto Armida Roma...

Public university in Irbid, Jordan This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Yarmouk University – news · newspapers · books · scholar · JSTOR (Januar...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber:&#...

Gajah india Gajah india Status konservasi Terancam (IUCN 3.1) Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mamalia Ordo: Proboscidea Famili: Elephantidae Genus: Elephas Spesies: Elephas maximus Subspesies: E. m. indicus Nama trinomial Elephas maximus indicus(Cuvier), 1798 Gajah india adalah salah satu subspesies gajah asia. Gajah ini dapat ditemui di India, Nepal, Bangladesh, Bhutan, Myanmar, Thailand, Semenanjung Malaya, Laos, Tiongkok, Kamboja dan Vietnam. Bukti ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Bernardus Prasodjo (lahir 25 Januari 1945)[1] adalah seorang pelukis gambar kemasan produk makanan asal Indonesia. Ia dikenal sebagai pembuat gambar dari kemasan berbagai merek seperti Khong Guan, Monde, Nissin Wafer, dan logo Sirup Marjan. ...

German football player and manager (born 1938) This article contains weasel words: vague phrasing that often accompanies biased or unverifiable information. Such statements should be clarified or removed. (June 2010) Otto Rehhagel Rehhagel in 2010Personal informationDate of birth (1938-08-09) 9 August 1938 (age 85)Place of birth Essen, GermanyHeight 1.77 m (5 ft 10 in)Position(s) DefenderYouth career1948–1957 TuS Helene AltenessenSenior career*Years Team Apps (Gls)1957�...

Russian Old Believer minority group located in Romania, Ukraine, Moldova and Bulgaria Lipoveni redirects here. For Lipoveni (disambiguation), see Lipoveni (disambiguation). This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2016) (Learn how and when to remove this message) Ethnic group LipovansЛиповане (Russian)Flag of the LipovansLipovans dur...

Ivan DodigKebangsaan KroasiaTempat tinggalFreeport, BahamaLahir2 Januari 1985 (umur 39)Međugorje, BiHTinggi183 m (600 ft 5 in)Memulai pro2004Tipe pemainTangan kanan (backhand dua tangan)Total hadiah$9,052,100Situs web resmiivandodig.comTunggalRekor (M–K)118–140 (45.74% di level Tur ATP, level Grand Slam, dan di Piala Davis)Gelar1Peringkat tertinggiNo. 29 (7 Oktober 2013)Hasil terbaik di Grand Slam (tunggal)Australia Terbuka3R (2013)Prancis Terbuka2R (20...

Perotto (seduto a sinistra, in primo piano), con il team della P101 (eccetto Gaiti): De Sandre (seduto a destra), Garziera (in piedi a sinistra) e Toppi (in piedi a destra) Pier Giorgio Perotto (Torino, 24 dicembre 1930 – Genova, 23 gennaio 2002) è stato un ingegnere e informatico italiano. Progettista della Olivetti, fu un pioniere dell'informatica, noto soprattutto per aver progettato la Programma 101, il primo esempio di computer a programma memorizzato da tavolo[1][2] o...

Paradox ist eine Weiterleitung auf diesen Artikel. Weitere Bedeutungen sind unter Paradox (Begriffsklärung) aufgeführt. Das Penrose-Dreieck erweckt den Anschein, es handele sich um eine geschlossene dreidimensionale Struktur aus drei rechten Winkeln, was in der euklidischen Geometrie jedoch unmöglich ist. Ein Paradoxon (auch das Paradox oder die Paradoxie, Plural Paradoxa,Paradoxe bzw. Paradoxien; vom altgriechischen Adjektiv παράδοξος parádoxos „wider Erwarten, wider die gew�...