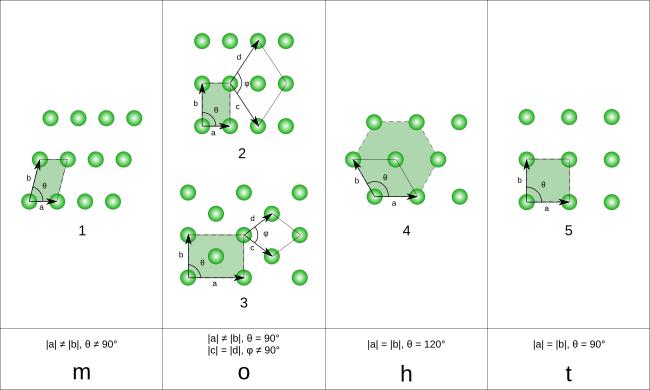
Kisi Bravais
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Radio station in Petersburg, Virginia WTPSSimulcasts WXGI RichmondPetersburg, VirginiaBroadcast areaMetro PetersburgFrequency1240 kHzBrandingThe BoxProgrammingFormatClassic hip hopOwnershipOwnerUrban One(Radio One Licenses, LLC)Sister stationsWCDX, WKJM, WKJS, WPZZ, WXGIHistoryFirst air date1945 (as WSSV)Former call signsWSSV (1945–1986)WPLZ (1986–1989)WGCV (1989–2003)WROU (2003–2007)Call sign meaningThe People's StationTechnical informationFacility ID60474ClassCPower1,000 watts unlim...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Slavyanskaya Square – news · newspapers · books · scholar · JSTOR (November 2006) (Learn how and when to remove this template message) Slavyanskaya Square after reconstruction in 2017. Slavyanskaya Square (Russian: Славянская площадь) is a squa...

Untuk kegunaan lain, lihat Sinus (disambiguasi). Aturan SinusDengan lingkaran luarTanpa lingkaran luarSegitiga yang diberi label menyesuaikan dengan aturan sinus. Nilai sudut α, β dan γ masing-masing berasosiasi dengan titik sudut A, B, dan C. Huruf kecil a, b, dan c adalah panjang dari sisi yang menghadap sudut-sudut tersebut. (sisi a menghadap sudut α, dst.)Dalam trigonometri, aturan sinus, rumus sinus, atau hukum sinus adalah sebuah persamaan yang memperbandingan panjang sisi-sisi segi...

Chemical compound BenserazideClinical dataOther namesSerazide, RO 4-4602AHFS/Drugs.comInternational Drug NamesPregnancycategory AU: B3 ATC codeNoneIdentifiers IUPAC name (RS)-2-Amino-3-hydroxy-N′-(2,3,4-trihydroxybenzyl)propanehydrazide CAS Number322-35-0 Yas HCl: 14919-77-8PubChem CID2327IUPHAR/BPS5150DrugBankDB12783as HCl: DBSALT002687ChemSpider2237 Yas HCl: 25109UNII762OS3ZEJUas HCl: B66E5RK36QKEGGD03082 YChEBICHEBI:64187as HCl: CHEBI:31262ChE...

إدوارد أوسكار أولريش معلومات شخصية الميلاد 1 فبراير 1857 كوفينغتون الوفاة 22 فبراير 1944 (87 سنة) واشنطن العاصمة مواطنة الولايات المتحدة عضو في الأكاديمية الوطنية للعلوم الحياة العملية اختصار اسم علماء النبات E.O.Ulrich المهنة إحاثي، وعالم نبات مج�...

1828 Connecticut gubernatorial election ← 1827 April 10, 1828 1829 → Nominee Gideon Tomlinson Party National Republican Popular vote 9,297 Percentage 97.73% County results Tomlinson: >90% Governor before election Gideon Tomlinson Democratic-Republican Party (Tomlinson Faction) Elected Governor Gideon Tomlinson National Republican Elections in Connecticut Federal government U.S President 1788–89 1792 1796 1800 1804 1808 1812...

English novelist, biographer and journalist (1904–1973) For the American biographer, see Nancy Milford. The HonourableNancy MitfordCBEMitford in 1932BornNancy Freeman-Mitford(1904-11-28)28 November 1904London, EnglandDied30 June 1973(1973-06-30) (aged 68)Versailles, FranceOccupationNovelistbiographerNotable worksThe Pursuit of LoveLove in a Cold ClimateNoblesse Oblige (ed.)Spouse Peter Rodd (m. 1933; div. 1957)ParentDavid Mitford, 2nd...

Early history of Texas A&M University–Commerce History of ETSTC redirects here. For the history of the former East Tennessee State Teachers College, see East Tennessee State University § History. Aerial view of ETSTC in 1941 The history of East Texas State Teachers College (ETSTC) comprises the history of the university now known as Texas A&M University–Commerce from its renaming as East Texas State Teachers College in 1923 (to define its purpose more clearly) to its renamin...

Radio station in Baltimore, MarylandWWINBaltimore, MarylandBroadcast areaBaltimore metropolitan areaFrequency1400 kHzBrandingSpirit 1400 AMProgrammingFormatUrban GospelOwnershipOwnerUrban One(Radio One Licenses, LLC)Sister stationsWERQ-FM, WOLB, WWIN-FMHistoryFirst air date1951; 73 years ago (1951)Technical informationFacility ID54709ClassCPower500 wattsLinksWebsitemybaltimorespirit.com WWIN (1400 kHz) is a commercial AM radio station in Baltimore, Maryland. Owned by Urban O...

Academic journalMexican Studies/Estudios MexicanosDisciplineMultidisciplinaryLanguageEnglish, SpanishEdited byChristian ZlolniskiPublication detailsHistory1985–presentPublisherUniversity of California Press on behalf of the University of California Institute for Mexico and the United States and the Universidad Nacional Autónoma de MéxicoFrequencyTriannualStandard abbreviationsISO 4 (alt) · Bluebook (alt1 · alt2)NLM (alt) · MathSciNet (alt )IS...

Athletics at the Olympics Men's 2590 metres steeplechaseat the Games of the III OlympiadGold medalist Jim LightbodyVenueFrancis FieldDatesAugust 29Competitors7 from 2 nationsMedalists Jim Lightbody United States John Daly Great Britain Arthur L. Newton United States Athletics at the1904 Summer OlympicsTrack events60 mmen100 mmen200 mmen400 mmen800 mmen1500 mmen110 m hurdlesmen200 m hurdlesmen400 m hurdlesmen2590 m steeplechasemen4 mile team racemenRoad eventsMarath...

American college basketball season 2010–11 Vanderbilt Commodores men's basketballNCAA tournament, Round of 64ConferenceSoutheastern ConferenceRankingAPNo. 25Record23–11 (9–7 SEC)Head coachKevin StallingsAssistant coaches Brad Frederick Dan Muller King Rice Home arenaMemorial GymnasiumSeasons← 2009–102011–12 → 2010–11 Southeastern Conference men's basketball standings vte Conf Overall Team W L PCT W L PCT East No. 15 ...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kagoshima District, Kagoshima – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Kagoshima (鹿児島郡, Kagoshima-gun) is a district located in Kagoshima Prefecture, Japan. As of October 1, 2008, the district has an estima...

Larinioides patagiatus Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Arachnida Ordo: Araneae Famili: Araneidae Spesies: Larinioides patagiatus Nama binomial Larinioides patagiatusClerck, 1757 Larinioides patagiatus adalah spesies laba-laba yang tergolong famili Araneidae. Spesies ini juga merupakan bagian dari ordo Araneae. Nama ilmiah dari spesies ini pertama kali diterbitkan pada tahun 1757 oleh Clerck. Laba-laba ini biasanya banyak ditemui di Holarktik. Referensi Platnick...

2007 Parti Québécois leadership election ← 2005 26 June 2007 2015 → Candidate Pauline Marois Party Parti Québécois Popular Vote Acclaimed Leader before election André Boisclair Elected Leader Pauline Marois The Parti Québécois leadership election of 2007 elected the seventh leader of the Parti Québécois, the main political party to promote Quebec independence in Quebec, Canada, and was won by Pauline Marois. Former PQ Minister Pauline Marois was the firs...

1998 – MCMXCVIII26 år sedan År1995 | 1996 | 199719981999 | 2000 | 2001 Årtionde1970-talet | 1980-talet 1990-talet2000-talet | 2010-talet Århundrade1800-talet 1900-talet2000-talet Årtusende1000-talet Året Födda | AvlidnaBildanden | Upplösningar Humaniora och kultur Datorspel | Film | Konst | Litteratur | Musik | Radio | Serier | Teater | TV Samhällsvetenskapoch samhälleKrig | Politik | Sport Teknik och vetenskapMeteo...

Traditional Hawaiian subdivision of land Moku redirects here. For the Estonian village, see Moku, Estonia. Full map of the ahupuaʻa of Oʻahu Closer view of the ahupuaʻa of Oʻahu's south and east side Ahupuaʻa (pronounced [əhupuˈwɐʔə]) is a Hawaiian term for a large traditional socioeconomic, geologic, and climatic subdivision of land (comparable to the tapere in the Southern Cook Islands). It usually extends from the mountains to the sea and generally includes one or more co...

John GreenwoodBorn4 February 1821Ryshworth Hall, BradfordDied21 February 1874Pimlico, MiddlesexNationalityEnglishOccupationPoliticianEmployerself-employed;SpouseLouisa Elizabeth BarnardistonChildrenFrederick Barnardiston Greenwood, Charles Staniforth Greenwood, Edwin Wilfred Greenwood, Hubert John Greenwood, Clara Louisa GreenwoodParent(s)Frederick Greenwood, Sarah Staniforth John Greenwood (born 4 February 1821 in Ryshworth Hall, near Bradford; died 21 February 1874, Pimlico, Middlesex) was ...

Indian politician Udai BhanPresident of the Haryana Pradesh Congress CommitteeIncumbentAssumed office 27 April 2022Preceded bySelja KumariMember of the Haryana Legislative AssemblyIn officeOctober 2014 – October 2019Preceded byJagdish NayarSucceeded byJagdish NayarConstituencyHodalIn office2000–2009Preceded byJagdish NayarSucceeded byJagdish NayarConstituencyHassanpur Personal detailsBorn (1955-11-02) 2 November 1955 (age 68)Hodal, Punjab, India(now in Haryana, India)Pol...

Pour les articles homonymes, voir Internationale (politique) et IS. Ne doit pas être confondu avec Internationale ouvrière socialiste. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (février 2010). Vous pouvez améliorer la vérif...