Szakóca
|
Read other articles:
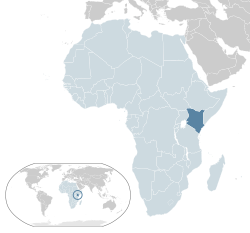
artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Untuk kegunaan lain, lihat Kenya (disambiguasi).Republik KenyaJamhuri ya Kenya (Swahili) Bendera Lambang Semboyan: Harambee (Swahili: Mari be...

Bagian dari seriAgama Hindu Umat Sejarah Topik Sejarah Mitologi Kosmologi Dewa-Dewi Keyakinan Brahman Atman Karmaphala Samsara Moksa Ahimsa Purushartha Maya Filsafat Samkhya Yoga Mimamsa Nyaya Waisesika Wedanta Dwaita Adwaita Wisistadwaita Pustaka Weda Samhita Brāhmana Aranyaka Upanishad Wedangga Purana Itihasa Bhagawadgita Manusmerti Arthasastra Yogasutra Tantra Ritual Puja Meditasi Yoga Bhajan Upacara Mantra Murti Homa Perayaan Dipawali Nawaratri Siwaratri Holi Janmashtami Durgapuja Nyepi...

Baharuddin Lopa Menteri Kehakiman dan Hak Asasi Manusia Indonesia ke-23Masa jabatan9 Februari 2001 – 2 Juni 2001PresidenAbdurrahman Wahid PendahuluYusril Ihza MahendraPenggantiMarsillam SimanjuntakJaksa Agung Republik Indonesia ke-17Masa jabatan6 Juni 2001 – 3 Juli 2001PresidenAbdurrahman Wahid PendahuluMarzuki DarusmanPenggantiMarsillam SimanjuntakBupati Majene ke-1Masa jabatan1960–1961PresidenSoekarnoGubernurAndi Pangerang Petta Rani PendahuluTidak ada, j...

2016 studio album by RadioheadA Moon Shaped PoolStudio album by RadioheadReleased8 May 2016 (2016-05-08)RecordedSeptember 2014–2016Studio La Fabrique, Saint-Rémy-de-Provence, France RAK, London Radiohead studio, Oxfordshire Genre Art rock folk chamber ambient baroque pop post-rock Length52:31LabelXLProducerNigel GodrichRadiohead chronology The King of Limbs: Live from the Basement(2011) A Moon Shaped Pool(2016) OK Computer OKNOTOK 1997 2017(2017) Singles from A Moon...

Site of Special Scientific Interest in Kent, England Lynsore BottomSite of Special Scientific InterestLocationKentGrid referenceTR 160 479[1]InterestBiologicalArea70.6 hectares (174 acres)[1]Notification1985[1]Location mapMagic Map Lynsore Bottom is a 70.6-hectare (174-acre) biological Site of Special Scientific Interest north of Folkestone in Kent.[1][2] These coppice with standards woods have a variety of tree species. The ground flora is diverse, and...

Collaborative mapping tool Google Map MakerScreenshot Screenshot of the town of Ísafjörður, Iceland, in Google Map MakerType of siteWeb mappingAvailable inMultilingualSuccessor(s)Google My MapsOwnerGoogleURLwww.google.com/mapmaker[1]RegistrationYesLaunchedJune 23, 2008; 15 years ago (2008-06-23)Current statusDefunct March 31, 2017; 7 years ago (2017-03-31) Google Map Maker was a map editing service launched by Google in June 2008.[2...

Light boat that is paddled This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Folding kayak – news · newspapers · books · scholar · JSTOR (October 2012) (Learn how and when to remove this message) A folding kayak is a direct descendant of the original Inuit kayak made of animal skins stretched over frames made ...

American baseball player Baseball player John CandelariaPitcherBorn: (1953-11-06) November 6, 1953 (age 70)Brooklyn, New York, U.S.Batted: LeftThrew: LeftMLB debutJune 8, 1975, for the Pittsburgh PiratesLast MLB appearanceJuly 7, 1993, for the Pittsburgh PiratesMLB statisticsWin–loss record177–122Earned run average3.33Strikeouts1,673 Teams Pittsburgh Pirates (1975–1985) California Angels (1985–1987) New York Mets (1987) New York Yankees (1988–1989...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

莎拉·阿什頓-西里洛2023年8月,阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日(46歲) 美國佛羅里達州国籍 美國别名莎拉·阿什頓(Sarah Ashton)莎拉·西里洛(Sarah Cirillo)金髮女郎(Blonde)职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人(2020年)《Political.tips》(2020年—)《LGBTQ國度》(2022年3月—2022年10月)烏克蘭媒�...

Gopal Bhar (bahasa Bengali: গোপাল ভাঁড়) adalah seorang pendongeng istana yang legendaris dan hidup masa pada abad pertengahan di Bengali. Dia tinggal di istana Raja Krishnachandra, raja terkenal di Nadia. Cerita-ceritanya terus dituturkan hingga kini di Bengali Barat dan Bangladesh. Dia terkenal atas kecerdasannya yang melampaui orang-orang di sekitarnya. Cerita-ceritanya disamakan dengan karya-karya Birbal dan Molla Nasiruddin. Statue of Gopal Bhar Patungnya bisa dil...

NGC 4386 الكوكبة التنين[1] رمز الفهرس NGC 4386 (الفهرس العام الجديد)MCG+13-09-027 (فهرس المجرات الموروفولوجي)PGC 40378 (فهرس المجرات الرئيسية)UGC 7491 (فهرس أوبسالا العام)2MASX J12242831+7531440 (Two Micron All-Sky Survey, Extended source catalogue)Z 352-33 (فهرس المجرات وعناقيد المجرات)Z 1222.1+7549 (فهرس المجرات وعناقيد المجر�...

Type of charitable organization See also: Foundation (nonprofit) Private FoundationChart of a foundationTypeCharitable organization A private foundation is a tax-exempt organization that does not rely on broad public support and generally claims to serve humanitarian purposes.[1][2][3] Unlike a charitable foundation, a private foundation does not generally solicit funds from the public or have the legal requirements and reporting responsibilities of a registered non-pr...

Pleasant emotional state Beim Heurigen in Grinzing is a typical scene of Gemütlichkeit, painting by Rudolf Alfred Höger (1900). Interior of the Café Hawelka with plush furniture and muted colours, serving cake and coffee, is a typical example of Gemütlichkeit. A cosy Stube normally has many wooden elements, giving a feeling of warmth and comfort (inside of Schreiberhaus in Neustift am Walde, Vienna). Hofbräukeller garden in Munich, a typical German beergarden scene, permeated by Gemütli...

Elections in California Federal government U.S. President 1852 1856 1860 1864 1868 1872 1876 1880 1884 1888 1892 1896 1900 1904 1908 1912 1916 1920 1924 1928 1932 1936 1940 1944 1948 1952 1956 1960 1964 1968 1972 1976 1980 1984 1988 1992 1996 Dem Rep 2000 Dem Rep 2004 Dem Rep 2008 Dem Rep 2012 Dem Rep 2016 Dem Rep 2020 Dem Rep 2024 Dem Rep U.S. Senate 1849 1850 1852 sp 1856 1857 sp 1860 1860 sp 1868 1872 1873 1873 sp 1878 1880 1885 1886 sp 1887 1891 1891 sp 1893 1895 sp 1897 1900 sp 1903 190...

Pour les articles homonymes, voir Gouvion et Saint-Cyr. Pour les autres membres de la famille, voir Famille de Gouvion Saint-Cyr. Laurent Gouvionmarquis de Saint-Cyr Portrait par Horace Vernet, 1821. Surnom « L'homme de glace »« Le Hibou »« Le mauvais coucheur » Naissance 13 avril 1764Toul (Trois-Évêchés) Décès 17 mars 1830 (à 65 ans)Hyères, Var ( Royaume de France) Origine Français Allégeance République française Empire françai...

Herman Dirk TielmanLahir(1904-09-02)2 September 1904Kampung Baru, Manado, Sulawesi Utara, IndonesiaMeninggal14 Mei 1979(1979-05-14) (umur 74)Den Haag, Amsterdam, BelandaPekerjaanTentara KNIL, PemusikSuami/istriNora Tielman (cerai) Flora Laurentine Hess (1935–1979)Anak1. Reggy Tielman (Reginald) [20 Mei 1933 - 12 Maret 2014 (80)] 2. Ponthon Tielman [04 Agustus 1934 - 29 April 2000 (65)] 3. Andy Tielman (Herman Hendrik Aadrian) [30 Mei 1936 - 10 November 2011 (75)] 4. Loulou Tielman (He...

Slovenian writer, poet, and screenwriter (born 1959) Feri LainščekBornFranc Lainšček (1959-10-05) October 5, 1959 (age 64)Dolenci, Socialist Federal Republic of Yugoslavia (now Slovenia)OccupationWriter, poet, screenwriterNationalitySlovenianNotable worksRooster's Breakfast Feri Lainšček (born 5 October 1959) is a Slovenian writer, poet, and screenwriter.[1] Early life He was born Franc Lainšček in a Slovene Lutheran family in the village of Dolenci (part of Šalovci), in...

北の国から ロケーション撮影に使用された五郎の家。初代丸太小屋(上)。3番目に建てられた家(下)。いずれも麓郷の森に移築。ジャンル テレビドラマ原作 倉本聰脚本 倉本聰演出 富永卓二杉田成道山田良明(連続ドラマ)杉田成道(SPドラマ)出演者 田中邦衛吉岡秀隆中嶋朋子原田美枝子岩城滉一地井武男いしだあゆみ大友柳太郎大滝秀治竹下景子 他製作制作 �...

Mathematical parametrization of vector spaces by another space The (infinitely extended) Möbius strip is a line bundle over the 1-sphere S1. Locally around every point in S1, it looks like U × R (where U is an open arc including the point), but the total bundle is different from S1 × R (which is a cylinder instead). In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X {\di...



