Rasch-modell
|
Read other articles:

Aleks Vrteski Informasi pribadiNama lengkap Aleksander VkteskiTanggal lahir 28 September 1988 (umur 35)Tempat lahir Karratha, AustraliaTinggi 1,94 m (6 ft 4+1⁄2 in)Posisi bermain GoalkeeperInformasi klubKlub saat ini Solo FCNomor 20Karier junior Future Glory AISKarier senior*Tahun Tim Tampil (Gol)2006–2007 Perth Glory 9 (0)2007–2009 FK Pobeda 20 (0)2009–2010 Perth Glory 4 (0)2010– Solo FC 0 (0)Tim nasional‡2005 Australia U-17 4 (0)2007 Australia U-20 1 (0)...

Adel Imam.LahirAdel Mohammed Imam Adel Emam (Arab: عادل إمامcode: ar is deprecated ) (lahir 17 Mei 1940) merupakan pemeran berkebangsaan Mesir. Kariernya terentang selama 45 tahun dengan berbagai peran di layar lebar. Filmografi Bobbos (2009) Hassan dan Marcus (2008) Morgan Ahmed Morgan (2007) The Yacoubian Building (2006) El Sefara fi El Imara (2005) Aris Min Jeha Amneya (2004) El Tagrubah El Denemarkiyah (2003) Amir El Zalam (2002) Al Wad Mahrous Beta'a Al Wazeer (1999) Hello Ameri...

Kejuaraan Bulu Tangkis Pan AmerikaSitus web resmiDidirikan1977; 47 tahun lalu (1977)Edisi27 (2024)LokasiKota Guatemala (2024)GuatemalaTempatGimnasium Teodoro Palacios Flores (2024)PutraPeserta64S / 32D / 8TJuara terkiniBrian Yang (tunggal)Adam DongNyl Yakura (ganda)Kanada (beregu)Gelar tunggal terbanyak3Osleni GuerreroKevin CordónGelar ganda terbanyak5Nyl YakuraGelar beregu terbanyak5KanadaPutriPeserta64S / 32D / 6TJuara terkiniMichelle Li (tunggal)Catherine ChoiJosephine Wu (ganda)Kana...

Kolombia adalah sebuah negara kesatuan yang terbagi dalam 32 departemen (bahasa Spanyol: departamentos, tunggal - departamento) dan sebuah Daerah Ibukota (Distrito Capital). Setiap departemen dipimpin oleh seorang gubernur (gobernador) dan memiliki dewan perwakilan, yang dipilih oleh rakyat untuk periode jabatan empat tahun. Gubernur tidak dapat dipilih kembali untuk periode yang berturutan. Departemen-departemen tersebut merupakan pembagian administratif negara yang mendapatkan status otonom...

Johannes TropfkeJohannes Tropfke[1]BiographieNaissance 14 octobre 1866BerlinDécès 10 novembre 1939 (à 73 ans)BerlinNationalité allemandeFormation Université Martin-Luther de Halle-WittembergActivités Mathématicien, historien des mathématiquesAutres informationsMembre de Académie internationale d'histoire des sciencesDirecteur de thèse Lazarus FuchsDistinctions Prix Alfred Ackermann-Teubner (1930)Médaille Leibniz d'argent (1939)modifier - modifier le code - modifier Wikidata Jo...
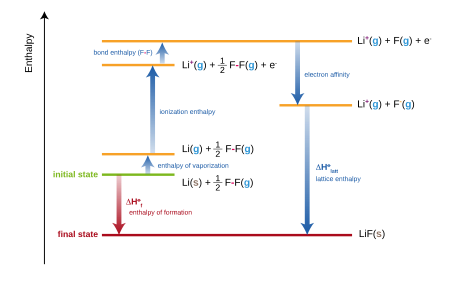
Change of enthalpy during the formation of a compound from its elements In chemistry and thermodynamics, the standard enthalpy of formation or standard heat of formation of a compound is the change of enthalpy during the formation of 1 mole of the substance from its constituent elements in their reference state, with all substances in their standard states. The standard pressure value p⦵ = 105 Pa (= 100 kPa = 1 bar) is recommended by IUPAC, although prior to 1982 the value 1.00 atm (101.325...

Mary Edwards Walker (lahir pada tanggal 26 November 1832 di Oswego, New York, Amerika Serikat-meninggal pada tanggal 21 Februari 1919) adalah seorang feminis Amerika, tawanan perang dan sorang ahli bedah hingga biasa disebut Dr. Mary Walker. Ia juga merupakan satu-satunya wanita yang menerima Medal of Honor.[1] Ia memperoleh gelar doktor di Syracuse Medical College di New York, pada tahun 1855. Lalu ia menikah dengan Albert Miller dan memulai karir doktornya dengan membuka praktik di ...

Renoult in 1931 René Renoult (29 August 1867 in Paris – 30 April 1946 in Paris) was a French Minister and lawyer.[1] Renoult was the son of Étienne and Élisa Geranger, a female day laborer. He studied at the Faculty of Law in Paris and obtained his doctorate in 1888. He married for the first time with Blanche-Clothilde Wormser in 1910, and a second time with Henriette-Emelie-Céleste Giriat in 1937. Renoult was a member of the Radical Party. His political career started in 1...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Форма́льная систе́ма (форма́льная тео́рия, аксиоматическая теория, аксиоматика, дедуктивная система) — результат строгой формализации теории, предполагающей полную абстракцию от смысла слов используемого языка, причём все условия, регулирующие употребление этих с�...

Charlotte-Frédérique de Mecklembourg-SchwerinTitres de noblesseDuchesse de Mecklembourg-Schwerin (d)Hereditary Princess (d)BiographieNaissance 4 décembre 1784LudwigslustDécès 13 juillet 1840 (à 55 ans)RomeSépulture Localisation inconnue (d)Nom dans la langue maternelle Charlotte Friederike, Herzogin zu Mecklenburg-SchwerinNationalité Grand-duché de Mecklembourg-SchwerinActivité SalonnièreFamille Maison de MecklembourgPère Frédéric-François Ier de Mecklembourg-Schwerin...

Response to the same environmental variation differently by different genotypes GXE redirects here. For the aircraft, see Waco GXE. Gene–environment interaction (or genotype–environment interaction or G×E) is when two different genotypes respond to environmental variation in different ways. A norm of reaction is a graph that shows the relationship between genes and environmental factors when phenotypic differences are continuous.[1] They can help illustrate GxE interactions. When...

Material that breaks up into parts instead of deforming as one This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Frangibility – news · newspapers · books · scholar...

Islands redirects here. For other uses, see Islands (disambiguation). An aerial view of islands in the Seychelles This is a list of the lists of islands in the world grouped by country, by continent, by body of water, and by other classifications. For rank-order lists, see the other lists of islands below. Lists of islands by country Africa Ascension Island (United Kingdom) Algeria Angola British Indian Ocean Territory (United Kingdom) Cape Verde Comoros Djibouti Equatorial Guinea Eritrea Et...

Imperial dynasty in Vietnam from 1428 to 1789 For the earlier Lê dynasty who ruled from 980 to 1009, see Early Lê dynasty. This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Lê dynasty – news · newspapers · books · scholar · JSTOR (December 2020) (Learn how and when to remove this message) Great Việt大越國Đại Việt Quốc1428–15271533–1789M...

Third son of Adam and Eve This article is about the third son of Adam and Eve. For the Egyptian deity, see Set (deity). For other uses, see Seth (disambiguation). SethFresco of Forefather Sif (1378), by Theophanes the Greek, in the Church of the Transfiguration of the Savior in Novgorod.PersonalBorn3874 (in Julian calendar) BC, 3670 (in Julian calendar) BC Died2962 (in Julian calendar) BC, 2758 (in Julian calendar) BC SpouseAzura ChildrenEnos, Noam ParentsAdam (fath...

Seluruh wilayah di Sulawesi Utara Masih Beroperasi (On Air) FM & AM Logo Nama Frekuensi Jaringan Alamat Milik RRI Pro 1 Manado 94.5 MHz & 88.2 MHz RRI Programa 1 & RRI Programa 3 Tikala Ares LPP Radio Republik Indonesia RRI Pro 1 Tahuna 105.4 MHz & 99.5 MHz RRI Programa 1 & RRI Programa 3 Tona Satu LPP Radio Republik Indonesia RRI Pro 1 Talaud 101.2 MHz RRI Programa 1 & RRI Programa 3 Melonguane LPP Radio Republik Indonesia RRI Pro 2 Manado 97.7 MHz RRI Programa 2 Tik...

Extended and increasing shortage since 1970 A tent city, a form of improvised housing, in Oakland, California Since about 1970, California has been experiencing an extended and increasing housing shortage,[1]: 3 such that by 2018, California ranked 49th among the states of the U.S. in terms of housing units per resident.[2]: 1 [3] This shortage has been estimated to be 3-4 million housing units (20-30% of California's housing stock, 14 ...

Kewalirajaan Mesirالخديوية المصرية (Arab) خدیویت مصر (Turki Utsmani)1867–1914 Bendera (1867–81) Lambang Lagu kebangsaan: Salam AffandinaGlobe dengan batas negara modern dengan keterangan: Kekhudaiwian Mesir Kondominium Sudan Inggris-Mesir Diserahkan dari Sudan ke Afrika Utara Italia pada 1919StatusNegara taklukan otonom dari Kesultanan Utsmaniyah(di bawah pendudukan Britania Raya dari tahun 1882)Ibu kotaKairoBahasa yang u...

Ashley Rae Fink Ashley Rae Fink (Houston, 20 novembre 1986) è un'attrice statunitense. Indice 1 Biografia 2 Filmografia 2.1 Cinema 2.2 Televisione 3 Note 4 Altri progetti 5 Collegamenti esterni Biografia Nasce a Houston, in Texas, e inizia a recitare all'età di 4 anni nello spettacolo estivo della sua scuola.[1] Dopo essersi trasferita con la famiglia a Los Angeles, si dedica totalmente alla recitazione e frequenta il Arts High School, dove si esibisce davanti ad un pubblico più va...






