Palindromszámok
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Blood BankAlbum mini karya Bon IverDirilis20 Januari 2009DirekamDesember 2006 – Juni 2008StudioPondok berburu (Dunn County, WI)Ticonderobics (Raleigh, NC)Apartemen Chris dan Jesse (Montreal, QC)Otter Creek Rd. (Fall Creek, WI)Rumah kecil (Eau Claire, WI)GenreIndie folkDurasi16:54LabelJagjaguwarProduserJustin VernonKronologi Bon Iver For Emma, Forever Ago(2007) Blood Bank(2009) Bon Iver(2011) Sampul alternatif Penilaian profesional Skor ulasan Sumber Nilai AbsolutePunk 91% [1] Al...

Diagram buret modern Buret adalah sebuah peralatan gelas laboratorium berbentuk silinder yang memiliki garis ukur dan sumbat keran pada bagian bawahnya. Ia digunakan untuk meneteskan sejumlah reagen cair dalam eksperimen yang memerlukan presisi, seperti pada eksperimen titrasi. Buret sangatlah akurat, buret kelas A memiliki akurasi sampai dengan ± 0,05 cm3. Buret Shelbach Oleh karena presisi buret yang tinggi, kehati-hatian pengukuran volume dengan buret sangatlah penting untuk menghind...

Cet article est une ébauche concernant la Vienne et le domaine des archives. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Archives départementales de la VienneCadreType Archives départementalesPays FranceCoordonnées 46° 34′ 01″ N, 0° 22′ 19″ EOrganisationEffectif 19,4 employés (2021), 19,6 employés (2020), 19,6 employés (2019), 20 employés (2018), 19 emplo...
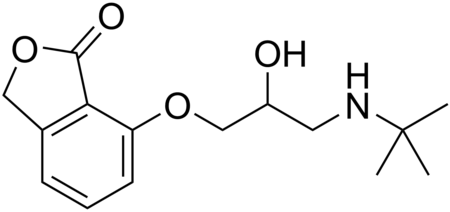
Chemical compound AfurololClinical dataATC codenoneIdentifiers IUPAC name 7-[3-(tert-Butylamino)-2-hydroxy-propoxy]-3H-isobenzofuran-1-one CAS Number65776-67-2 NPubChem CID176877ChemSpider154050 YUNIIWQ1WRV49R9ChEMBLChEMBL1742435 NChemical and physical dataFormulaC15H21NO4Molar mass279.336 g·mol−13D model (JSmol)Interactive image SMILES O=C1OCc2cccc(OCC(O)CNC(C)(C)C)c12 InChI InChI=1S/C15H21NO4/c1-15(2,3)16-7-11(17)9-19-12-6-4-5-10-8-20-14(18)13(10)12/h4-6,11,16-17H,7-9...

Abdurrahman BaswedanAR Baswedan Wakil Menteri Penerangan Indonesia ke-2Masa jabatan2 Oktober 1946 – 3 Juli 1947PresidenSoekarnoPerdana MenteriSutan Sjahrir PendahuluAli SastroamidjojoPenggantiSjahbudin Latif Informasi pribadiLahir(1908-09-09)9 September 1908 Surabaya, Hindia BelandaMeninggal16 Maret 1986(1986-03-16) (umur 77)Jakarta, IndonesiaMakamTPU Tanah KusirPartai politikPersatuan Arab Indonesia Partai MasyumiSuami/istriSjaichun (1925-1948)Barkah Ganis (1950-1986)Hubu...

لمعانٍ أخرى، طالع شهر أباد (توضيح). شهر أباد شهرآباد - city - تقسيم إداري البلد إيران المحافظة خراسان رضوي المقاطعة مقاطعة بردسكن الناحية شهر أباد إحداثيات 35°08′48″N 57°55′51″E / 35.14667°N 57.93083°E / 35.14667; 57.93083 السكان التعداد السكاني 2185 نسمة (إحصاء 2006) م...

Zoo in Staten Island, New York Staten Island ZooStaten Island Zoo LogoStaten Island Zoo Entrance40°37′30″N 74°06′54″W / 40.625°N 74.115°W / 40.625; -74.115Date openedJune 10, 1936Location614 Broadway, Staten IslandLand area8 acres (3.2 ha)No. of animals1400No. of species320MembershipsAssociation of Zoos and Aquariums (AZA)Major exhibitsAfrica, Tropical Forest, Reptile WingPublic transit accessBus: S48, S53Websitehttp://www.statenislandzoo.org The State...

Nepali writer and novelist (1914-1981) Bhawani Bhikshuभवानी भिक्षुBornNohor Ram Gupta(1914-06-03)3 June 1914Taulihawa, Kapilvastu, NepalDied16 April 1981(1981-04-16) (aged 66)Kathmandu, NepalOccupation(s)Writer, novelistNotable workAagatPipe no.2AwardsMadan Puraskar (1975)Sajha Puraskar (1975)Tribhuwan Pragya Puraskar 2036 BS (1979-1980) Nohor Ram Gupta, professionally known as Bhawani Bhikshu (Nepali: भवानी भिक्षु) was a Nepali writer, poet, l...

Italian TV series or program ValentinaGenreErotic thrillerBased onValentina by Guido CrepaxStarring Demetra Hampton Russel Case Antonello Fassari Mary Sellers Theme music composerFio ZanottiOpening themeValentinaComposerFio ZanottiCountry of originItalyOriginal languageItalianNo. of seasons1No. of episodes13 (list of episodes)ProductionExecutive producerRoberto CacciaguerraProducersAngelo Rizzoli, Jr.Production locationsMilanBarcelonaRunning time30 minutesOriginal releaseNetworkItalia 1Relea...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Artikel ini memiliki beberapa masalah. Tolong bantu memperbaikinya atau diskusikan masalah-masalah ini di halaman pembicaraannya. (Pelajari bagaimana dan kapan saat yang tepat untuk menghapus templat pesan ini) Biografi ini memerlukan lebih banyak catatan kaki untuk pemastian. Bantulah untuk menambahkan referensi atau sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus, khususnya jika berpotensi memfitnah.Cari sumber:...

Traudl JungeJunge pada 1945LahirGertraud Humps(1920-03-16)16 Maret 1920Munich, Bavaria, GermanyMeninggal10 Februari 2002(2002-02-10) (umur 81)Munich, Bavaria, JermanSebab meninggalKankerKebangsaanJermanPekerjaanSekretaris, wartawan ilmiah sub-editorTempat kerjaAdolf HitlerDikenal atasSekretaris pribadi Adolf Hitler pada masa Perang Dunia KeduaSuami/istriHans Junge (terbunuh saat bertugas pada 1944)AnaknoneOrang tuaMax Humps and Hildegard Humps (née Zottmann)KerabatSaudari; Inge Hu...

1927 silent film The King of KingsDirected byCecil B. DeMilleWritten byJeanie MacPhersonProduced byCecil B. DeMilleStarringH.B. WarnerDorothy CummingErnest TorrenceJoseph SchildkrautJames NeillCinematographyJ. Peverell MarleyF.J. WesterbergEdited byAnne BauchensHarold McLernonMusic byHugo RiesenfeldJosiah ZuroDistributed byPathé ExchangeRelease date April 19, 1927 (1927-04-19) Running time155 minutesCountryUnited StatesLanguagesSound (Synchronized) (English Intertitles)Budget$...

Islam menurut negara Afrika Aljazair Angola Benin Botswana Burkina Faso Burundi Kamerun Tanjung Verde Republik Afrika Tengah Chad Komoro Republik Demokratik Kongo Republik Kongo Djibouti Mesir Guinea Khatulistiwa Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Pantai Gading Kenya Lesotho Liberia Libya Madagaskar Malawi Mali Mauritania Mauritius Maroko Mozambik Namibia Niger Nigeria Rwanda Sao Tome dan Principe Senegal Seychelles Sierra Leone Somalia Somaliland Afrika Selatan ...
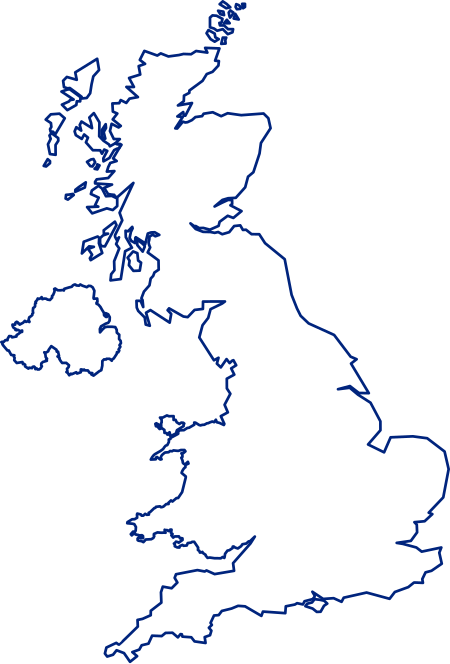
Untuk desa di Nottinghamshire, lihat Holbeck, Nottinghamshire. Koordinat: 53°47′20″N 1°33′18″W / 53.789°N 1.555°W / 53.789; -1.555 Holbeck Tegalan Holbeck dengan Bridgewater Place di latar Holbeck Letak Holbeck di West Yorkshire Ref. grid OS SE311314 Distrik metropolitan Kota Leeds County metropolitan West Yorkshire Region Yorkshire and the Humber Negara konstituen Inggris Negara berdaulat Britania Raya Kota pos LEEDS Distrik&#...

Village in Estonia Village in Rapla County, EstoniaVigala-VanamõisaVillageCountry EstoniaCountyRapla CountyParishMärjamaa ParishTime zoneUTC+2 (EET) • Summer (DST)UTC+3 (EEST) Vigala-Vanamõisa (Vanamõisa until 2017) is a village in Märjamaa Parish, Rapla County in western Estonia.[1] References ^ Classification of Estonian administrative units and settlements 2014[dead link] (retrieved 28 July 2021) vteSettlements in Märjamaa ParishBorough Märjamaa Vill...

Ezra 3Kitab Ezra (Kitab Ezra-Nehemia) (memuat Kitab Ezra dan Nehemia) lengkap pada Kodeks Leningrad, dibuat tahun 1008.KitabKitab EzraKategoriNevi'imBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen15← pasal 2 pasal 4 → Ezra 3 (disingkat Ezr 3) adalah bagian dari Kitab Ezra dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Memuat riwayat orang-orang yang pulang dari pembuangan ke Babel menurut catatan Ezra. Dalam Alkitab Ibrani termasuk dalam bagian Ketuvim...

Questa pagina contiene una traduzione, completa o parziale, della pagina originale:«Template:Phoenician cities and colonies» tratta da Wikipedia in inglese.La versione tradotta è la numero 564170989 del 14-07-2013. Consulta la cronologia della pagina originale per conoscere l'elenco degli autori.

Este artículo se refiere o está relacionado con una infraestructura de transporte público futura o en desarrollo. La información de este artículo puede cambiar frecuentemente. Por favor, no agregues datos especulativos y recuerda colocar referencias a fuentes fiables para dar más detalles. Callao La estación se construirá bajo el cruce de las Avenidas Callao y Santa Fe.UbicaciónDirección Avenida Callao y Avenida Santa FeSector Recoleta (Buenos Aires)Datos de la estaciónConexiones ...

French WW1 reconnaissance aircraft This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Morane-Saulnier P – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Type P/MS.21/MS.24/MS.26 Royal Flying Corps MS.24 Type P Role ReconnaissanceType of aircraft Manufactu...
