Másodrendű nyomaték
|
Read other articles:

Proklamasi Kemerdekaan Jamaika Koloni Jamaika memperoleh kemerdekaan dari Kerajaan Inggris pada 6 Agustus 1962. Di Jamaika, tanggal tersebut dirayakan sebagai Hari Kemerdekaan, sebuah hari libur nasional. Pulau ini menjadi koloni kerajaan pada 1509 ketika Spanyol menaklukan suku pribumi Taino. Pada 1655, pasukan Inggris mengambil alih pulau tanpa menerima perlawanan, kemudian Kerajaan Inggris mengklaim kepemilikan di atasnya. Selama bertahun-tahun, budak-budak yang kabur bergabung dengan prib...

Pertempuran ChamptoceauxBagian dari Perang Suksesi BrittaniaPerang Seratus TahunTanggal14–16 Oktober 1341LokasiChamptoceaux, Brittania PrancisHasil Kemenangan Prancis-BrittaniaPihak terlibat Wangsa Blois Prancis Wangsa MontfortTokoh dan pemimpin Charles dari Blois John de MontfortKekuatan 7.000+ Tidak diketahui, kecilKorban Tidak diketahui Tidak diketahui, banyak lbsPerang Suksesi Brittania Champtoceaux Brest Morlaix Saint-Pol-de-Léon La Roche-Derrien Tiga Puluh Mauron Auray Pertempuran Ch...

Guy HamiltonLahir(1922-09-16)16 September 1922Paris, PrancisMeninggal20 April 2016(2016-04-20) (umur 93)Mallorca, SpanyolPekerjaanSutradara filmTahun aktif1938–1989Suami/istriNaomi ChanceKerima Guy Hamilton (16 September 1922 – 20 April 2016) adalah seorang sutradara film asal Inggris. Ia aktif di dunia perfilman dari awal 1950-an sampai akhir 1980-an, dan sudah menyutradarai 22 film, termasuk diantaranya empat film James Bond (Goldfinger, Diamonds Are Forever, Li...
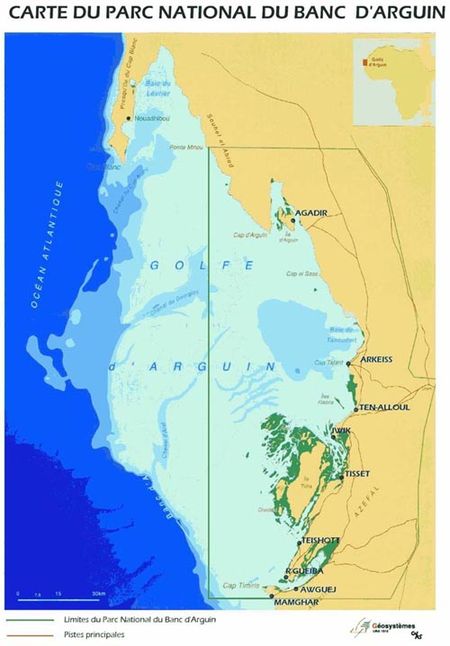
Bay on the coast of Mauritania Bay of ArguinBaie d'Arguin (French)Baía de Arguim (Portuguese)Map of the wider gulf area showing the Banc d'Arguin National ParkBay of ArguinLocation in MauritaniaCoordinates20°05′N 16°37′W / 20.08°N 16.62°W / 20.08; -16.62Ocean/sea sourcesAtlantic OceanBasin countriesMauritaniaMax. length13 km (8.1 mi)Max. width20 km (12 mi)IslandsÎle d’Arguin, Île de l'Ardent The Bay of Arguin (French: Bai...

Untuk film berjudul sama buatan tahun 1954, lihat: Malu-Malu Kutjing. Malu-Malu KucingSutradaraIshaq IskandarProduserLeonita SutopoDitulis olehTim Inem FilmPemeranMutia DatauHerman FelaniZainal AbidinPitrajaya BurnamaRieka SuatanBudi MoealamAmran S. MounaNoortje SupandiVivien SumaryoBaby JeannyPong HardjatmoSumi ArtyYos SantoHarry CapriUmar FaroukMariance MantouwPenata musikGatot SudartoSinematograferTjutju SutedjaPenyuntingSK SyamsuriDistributorInem FilmTanggal rilis1980Durasi126 menit...

Konten dan perspektif penulisan artikel ini hanya berpusat pada sudut pandang dari negara Indonesia dan tidak menggambarkan wawasan global pada subjeknya. Silakan bantu mengembangkan atau bicarakan artikel ini di halaman pembicaraannya, atau buat artikel baru, bila perlu. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Penduduk yang berkumpul di rumah Ketua Tonarigumi di Jepang Tonarigumi (Jepang: 隣組) atau dalam Bahasa Indonesia artinya kerukunan tetangga (sekarang...

Orang Maluku Thomas Matulessy Martha Christina Tiahahu Johannes Leimena Johannes Latuharhary Peter M. Christian Jacob Elfinus Sahetapy Stepanus Mahury George Toisutta Suaidi Marasabessy Alexander Litaay Bahlil Lahadalia Djauhari Oratmangun Daerah dengan populasi signifikan Indonesia: 2.203.415 (sensus 2010)[1] Maluku1.848.923Maluku Utara687.003Papua82.597Papua Barat78.855Jawa Barat47.886Daerah Khusus Ibukota Jakarta45.146Sulawesi Utara24.942Jawa Timur17.756Sulawesi Selatan15.884N...

Human settlement in EnglandAlsop en le DaleThe church at Alsop en le DaleAlsop en le DaleLocation within DerbyshireOS grid referenceSK160551Civil parishEaton and AlsopShire countyDerbyshireRegionEast MidlandsCountryEnglandSovereign stateUnited KingdomPost townAshbournePostcode districtDE6PoliceDerbyshireFireDerbyshireAmbulanceEast Midlands UK ParliamentDerbyshire Dales List of places UK England Derbyshire 53°05′36″N 1°45′42″W / 53.0933�...

Rookie Historian Goo Hae-ryungPoster promosiHangul신입사관 구해령 GenreSejarahRomansaDramaKomediDitulis olehKim Ho-sooSutradaraKang Il-sooHan Hyun-HeePemeranShin Se-kyungCha Eun-wooNegara asalKorea SelatanBahasa asliKoreaJmlh. episode40ProduksiProduserKim Sang-heonCho Hyung-jinPengaturan kameraSingle-cameraDurasi35 menitRumah produksiChorokbaem MediaDistributorMunhwa Broadcasting CorporationNetflixRilis asliJaringanMBC TVFormat audioDolby DigitalRilis17 Juli (2019-07-17) –...

Period of the history of Lithuania The Lithuanian National Revival, alternatively the Lithuanian National Awakening or Lithuanian nationalism (Lithuanian: Lietuvių tautinis atgimimas), was a period of the history of Lithuania in the 19th century at the time when a major part of Lithuanian-inhabited areas belonged to the Russian Empire (the Russian partition of the Polish–Lithuanian Commonwealth). It was expressed by the rise of self-determination of the Lithuanians that led to the formatio...
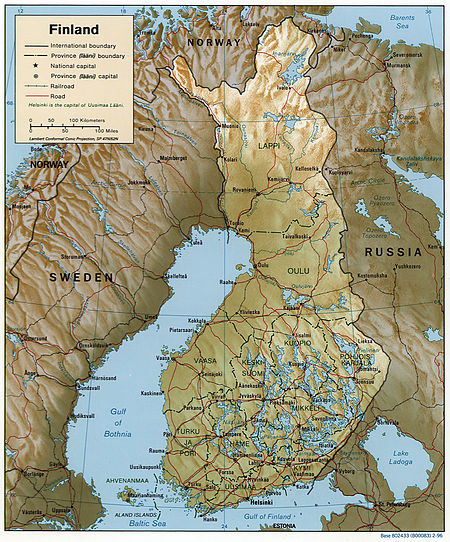
Overview of and topical guide to Finland See also: List of Finland-related topics The Flag of FinlandThe Coat of arms of Finland The location of Finland An enlargeable relief map of the Republic of Finland The following outline is provided as an overview of and topical guide to Finland. Finland – sovereign Nordic country located in Northern Europe.[1] Finland has borders with Sweden to the west, Russia to the east, and Norway to the north, while Estonia lies to its south across ...

Toray Pan Pacific Open 2018 Sport Tennis Data 17 – 23 settembre Edizione 43ª Superficie Cemento Campioni Singolare Karolína Plíšková Doppio Miyu Katō / Makoto Ninomiya 2017 2019 Il Toray Pan Pacific Open 2018 è stato un torneo di tennis giocato sul cemento indoor. È stata la 43ª edizione del Toray Pan Pacific Open, che fa parte della categoria Premier nell'ambito del WTA Tour 2018. Si è giocato all'Arena Tachikawa Tachihi di Tachikawa, in Giappone, dal 17 al 23 settembre 2018. In...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Nasi gandul – berita · surat kabar · buku · cendekiawan · JSTOR Nasi GandulNasi GandulNama lainSego GandulTempat asalIndonesiaDaerahPati, Jawa TengahSunting kotak info • L • BBantuan penggu...

Cet article est une ébauche concernant une chanson, la Suède et le Concours Eurovision de la chanson. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Hold Me Closer Chanson de Cornelia Jakobs auConcours Eurovision de la chanson 2022 Sortie 26 février 2022 Durée 3:19 Langue Anglais Genre Pop Auteur-compositeur Cornelia Jakobs, David Zandén, Isa Molin Classement 4e au Concours Eurovision de la chanson 20...

Questa voce sugli argomenti allenatori di pallacanestro statunitensi e cestisti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti dei progetti di riferimento 1, 2. Doug West Nazionalità Stati Uniti Altezza 198 cm Peso 91 kg Pallacanestro Ruolo Vice-allenatore(ex guardia / ala piccola) Squadra Westtown School f. Termine carriera 2001 - giocatore CarrieraGiovanili Altoona Area High School1985-1989 Villanova Wi...
Marit Mikkelsplass Nazionalità Norvegia Altezza 172 cm Peso 57 kg Sci di fondo Squadra Kjelsås IL Termine carriera 1998 Palmarès Competizione Ori Argenti Bronzi Olimpiadi 0 3 0 Mondiali 0 2 1 Per maggiori dettagli vedi qui Modifica dati su Wikidata · Manuale Marit Elisabeth Mikkelsplass nata Wold (Oslo, 22 febbraio 1965) è un'ex fondista norvegese, vincitrice di varie medaglie olimpiche e iridate. È moglie di Pål Gunnar, a sua volta fondista di alto livello[1]...

Annual festival in Cardiff, Wales Cardiff Design Festival is an annual event organised by the University of Wales Institute, Cardiff in partnership with a number of Cardiff organisations, which since its inception has included Design Wales, an organisation which has a pan Wales remit for supporting and encouraging the use of design. The Festival was first held in 2005,[1] within the City Centre at the Park Plaza Hotel on Cardiff's Greyfriars Road, as well as a number of other events a...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Species of vine Cucurbita digitata Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Cucurbitales Family: Cucurbitaceae Genus: Cucurbita Species: C. digitata Binomial name Cucurbita digitataGray Cucurbita digitata is a species of flowering plant in the squash family known by the common names fingerleaf gourd and bitter squash. It is similar to Cucurbita cali...

For the board game, see Jarmo (game). JarmoÇermoThe Neolithic village of Jarmo in Iraq, 1954Shown within Near EastShow map of Near EastJarmo (Iraq)Show map of IraqAlternative nameCharmoLocationChamchamal, Iraqi KurdistanRegionMesopotamiaCoordinates35°33′21″N 44°55′49″E / 35.55583°N 44.93028°E / 35.55583; 44.93028TypeSettlementArea12,000 to 16,000 m2 (170,000 sq ft)HistoryFoundedApproximately 7500 BCAbandonedApproximately 5000 BCPeriodsN...






















































