Metszési szám (gráfelmélet)
|
Read other articles:

Indonesian Choice Awards 2018Tanggal29 April 2018 (2018-04-29)LokasiSentul International Convention Center, BogorNegara IndonesiaDipersembahkan olehSarah SechanVincentDestaIkhtisarPenghargaan terbanyakSheila on 7 (2)Nominasi terbanyakIsyana SarasvatiRendy Pandugo (3)Album of the YearKereta Kencan – HIVI!Male Singer of the YearRendy PandugoFemale Singer of the YearRaisaActor of the YearAdipati DolkenActress of the YearChelsea IslanSitus webzulu.id/ica5/Siaran televisi/radioSaluranN...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Russian footballer (born 1987) In this name that follows Eastern Slavic naming customs, the patronymic is Vasilievich and the family name is Kudryashov. Fyodor Kudryashov Kudryashov with Russia in 2018Personal informationFull name Fyodor Vasilievich KudryashovDate of birth (1987-04-05) 5 April 1987 (age 37)Place of birth Mamakan, Russian SFSR, Soviet UnionHeight 1.81 m (5 ft 11 in)[1]Position(s) Left backYouth career1997–2002 Sibiryak BratskSenior career*Year...

gambar dari inti reaktor Triga. Perhatikan pendaran cahaya karena Radiasi Cherenkov. TRIGA adalah sebuah reaktor nuklir kelas kecil yang didesain dan dibuat oleh General Atomics dari Amerika Serikat. Nama TRIGA sendiri adalah kependekan dari Training, Research, Isotopes, General Atomics. Tim desain untuk TRIGA dipimpin oleh ahli fisika Freeman Dyson. Reaktor jenis ini sangat populer dan di Asia reaktor ini dimiliki oleh Indonesia, Thailand, Vietnam, Malaysia, Philipina, Korea, Jepang, Taiwan,...
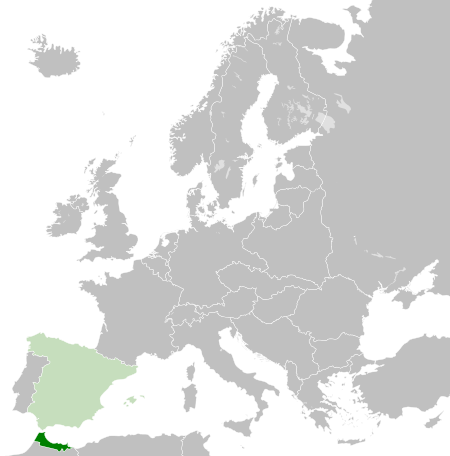
Spanish colonial army in Morocco For the French equivalent, see Army of Africa (France). Army of AfricaEjército de ÁfricaActive1912–1956Country SpainTypeArmyRoleLand forceSize35,000 personnel (1909)Part ofMinistry of Defence of Spain (from 1937)Garrison/HQTétouanEngagementsSecond Melillan campaignRif WarAsturian miners' strike of 1934Spanish Civil WarInvasion of Val d'AranIfni WarMilitary unit The Army of Africa (Spanish: Ejército de África, Arabic: الجيش الإسبان�...

كاستراكيون تقسيم إداري البلد اليونان [1] خصائص جغرافية إحداثيات 38°25′02″N 21°53′41″E / 38.41722222°N 21.89472222°E / 38.41722222; 21.89472222 الارتفاع 110 متر، و67 متر السكان التعداد السكاني 625 (resident population of Greece) (2021)538 (resident population of Greece) (2001)429 (resident population of Greece) (1991)670 (resident populat...

American faith-based film studio Affirm FilmsCompany typeSubsidiaryIndustryFilmTelevision programmingGenre Evangelical Christian Drama Kids & Family (starting with The Star) Biblical (starting with Risen) Horror & Thriller (starting with The Remaining) Founded2007; 17 years ago (2007)Headquarters10202 West Washington Boulevard. Stage #6-513 Culver City, California, U.S.Area servedWorldwideKey peopleRich Peluso (Executive Vice President)Tana Evans (Senior Vice Preside...

Memorial(RU) Мемориал TipoNon profit, ONG Fondazione28 gennaio 1989 FondatoreEsponenti di spicco del dissenso sovietico, tra cui Andrej Dmitrievič Sacharov ScopoDifesa dei diritti umani Sede centrale Mosca Area di azioneEx-Repubbliche dell'Unione Sovietica Presidente Sergei Kovalev Sito web e Sito web Modifica dati su Wikidata · Manuale Premio Nobel per la pace 2022 Memorial (Мемориал in russo) è un'associazione che ha sede a Mosca ed opera nelle ex Repubbliche del...

British talk show For the unrelated film, see Loose Women (film). Loose WomenAlso known asLive Talk (2000–2001)GenreTalk showCreated byDiane Nelmes[1]Presented by Ruth Langsford Kaye Adams Christine Lampard Charlene White StarringFull listCountry of originUnited KingdomOriginal languageEnglishNo. of seriesLoose Women: 28 Live Talk: 2ProductionExecutive producerEmma GormleyProducersHelen StuartEleanor Cotter (senior)Mattie Jameson (senior)Paul Pixton (senior)Harriet Thurley (senior)E...

Municipality in Bohol, Philippines Municipality in Central Visayas, PhilippinesBalilihanMunicipalityMunicipality of BalilihanBalilihan Municipal Hall FlagMap of Bohol with Balilihan highlightedOpenStreetMapBalilihanLocation within the PhilippinesCoordinates: 9°45′N 123°58′E / 9.75°N 123.97°E / 9.75; 123.97CountryPhilippinesRegionCentral VisayasProvinceBoholDistrict 1st districtFounded29 September 1828 previously part of Baclayon town.Barangays31 (see Barangays)...

2014 Taiwanese comedy film Sweet AlibisTraditional Chinese甜蜜殺機Simplified Chinese甜蜜杀机 Directed byLien Yi-chiStarringAlec SuAriel LinMatt WuLei HongLang Tsu-yunKen LinChu Chih-yingAustin LinKao Meng-chiehCinematographyRandy CheRelease date 17 January 2014 (2014-01-17) Running time112 minutesCountryTaiwanLanguagesMandarinTaiwanese Sweet Alibis is a 2014 Taiwanese comedy film starring Alec Su as a cowardly veteran cop and Ariel Lin as an overzealous rookie. The...

Railway station in West Bengal, India Canning Kolkata Suburban Railway StationCanning Railway StationGeneral informationLocationCanning, South 24 Parganas, West BengalIndiaCoordinates22°18′49″N 88°40′05″E / 22.313734°N 88.668119°E / 22.313734; 88.668119Elevation6 metres (20 ft)Owned byIndian RailwaysOperated byEastern RailwayLine(s)Canning Branch linePlatforms3Tracks3ConstructionStructure typeStandard (on-ground station)ParkingNot AvailableBicycle faci...

Province of Burundi Province in BurundiCibitoke ProvinceProvinceCountry BurundiCapitalCibitokeArea • Total1,635.52 km2 (631.48 sq mi)Population (2008 census) • Total460,435 • Density280/km2 (730/sq mi) Cibitoke Province is one of the 18 provinces of Republic of Burundi.[1] Communes It is divided administratively into the following communes: Commune of Buganda Commune of Bukinanyana Commune of Mabayi Commune of Mugina Co...

For the Birdbrain song, see Youth of America (Birdbrain song). 1981 studio album by WipersYouth of AmericaStudio album by WipersReleasedNovember 11, 1981[1]Recorded1980StudioWave Sound Studios, Vancouver, WashingtonGenre Punk rock post-punk proto-grunge[2] Length30:40LabelPark AvenueProducerGreg SageWipers chronology Alien Boy(1980) Youth of America(1981) Over the Edge(1983) Youth of America is the second studio album by American punk rock band Wipers. It was released ...

American diplomat, banker, businessman, industrialist, philanthropist, and art collector For the Irish sprinter, see Andrew Mellon (athlete). Andrew Mellon42nd United States Ambassador to the United KingdomIn officeApril 9, 1932 – March 17, 1933PresidentHerbert HooverFranklin D. RooseveltPreceded byCharles G. DawesSucceeded byRobert Worth Bingham49th United States Secretary of the TreasuryIn officeMarch 9, 1921 – February 12, 1932PresidentWarren G. HardingCalvin Coolidge...

В Википедии есть статьи о других людях с такой фамилией, см. Стариков. Иван Валентинович Стариков Дата рождения 16 августа 1960(1960-08-16) (63 года) Место рождения Пайвино, Пеньковский сельсовет, Маслянинский район, Новосибирская область, РСФСР, СССР Гражданство СССР Рос�...

Football tournament season 2001 Norwegian Football CupNorgesmesterskapet i fotball for herrerTournament detailsCountry NorwayTeams128 (main competition)Defending championsOdd GrenlandFinal positionsChampionsViking (5th title)Runner-upBryneTournament statisticsMatches played127Goals scored513 (4.04 per match)← 20002002 → Ullevaal Stadion, Oslo - venue for the Norwegian Cup final The 2001 Norwegian Football Cup was the 96th edition of the Norwegian Foot...

Aeropuerto de Aarhus Aarhus Lufthavn IATA: AAR OACI: EKAH FAA: LocalizaciónUbicación Kolind, DinamarcaElevación 25Sirve a AarhusDetalles del aeropuertoTipo CivilPropietario Aarhus (municipio)Operador Aarhus Lufthavn A/SPistas DirecciónLargoSuperficie10L/28R2.777Asfalto10R/28L2.702AsfaltoMapa AAR / EKAH Ubicación en DinamarcaSitio web https://www.aar.dk/[editar datos en Wikidata] El Aeropuerto de Aarhus (IATA: AAR, OACI: EKAH) es un aeropuerto civil ubicado en Tirstrup, Din...

Paper ClipEpisode The X-FilesNomor episodeMusim 3Episode 2SutradaraRob BowmanPenulisChris CarterKode produksi3X02Tanggal siar29 September 1995Durasi45 menitBintang tamu Mitch Pileggi sebagai Walter Skinner Walter Gotell sebagai Victor Klemper Melinda McGraw sebagai Melissa Scully Sheila Larken sebagai Margaret Scully Nicholas Lea sebagai Alex Krycek William B. Davis sebagai The Smoking Man John Neville sebagai Well-Manicured Man Tom Braidwood sebagai Melvin Frohike Dean Haglund sebagai R...

You Are a TouristSingel oleh Death Cab for Cutiedari album Codes and KeysDirilis29 Maret 2011[1]FormatDigital downloadGenreRock alternatif, indie rockDurasi4:46LabelAtlanticPenciptaBenjamin Gibbard You Are a Tourist adalah lagu dari band indie rock, Death Cab for Cutie dan dirilis sebagai singel pertama dari album Codes and Keys Video musik Pada tanggal 5 April 2011, band streaming pertunjukan live dari video musik untuk You Are a Tourist. Video, disutradarai oleh Tim Nackashi, itu di...







