Merev körű kiegészítés
|
Read other articles:
Perburuan rusa putih dari Chronicon Pictum, 1360. Menurut legenda Hungaria, Hunor dan Magor adalah nenek moyang orang Hun dan Magyar. Legenda ini pertama kali disebarkan oleh Gesta Hunnorum et Hungarorum. Tujuan legenda ini adalah untuk membuktikan bahwa orang Hun dan Magyar memiliki nenek moyang bersama. Orang-orang Magyar yang dipimpin oleh Pangeran Árpád telah menaklukkan wilayah Cekungan Carpathia pada tahun 890-an. Wilayah ini juga pernah ditaklukkan oleh Attila pada abad ke-5. Maka da...

Fanny Hill Salah satu edisi terawal, 1749 (MDCCXLIX)PengarangJohn ClelandJudul asliMemoirs of a Woman of PleasureNegaraBritania RayaBahasaInggrisGenreNovel erotisTanggal terbit21 November 1748; Februari 1749Jenis mediaCetak (sampul dan isi)OCLC13050889Desimal Dewey823/.6 19LCCPR3348.C65 M45 Ilustrasi Fanny Hill oleh Édouard-Henri Avril. Memoirs of a Woman of Pleasure (lebih populer dikenal sebagai Fanny Hill, anglikanisasi dari kata Latin mons veneris, bukit Venus)[1&...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2012. Artikel ini berisi konten yang ditulis dengan gaya sebuah iklan. Bantulah memperbaiki artikel ini dengan menghapus konten yang dianggap sebagai spam dan pranala luar yang tidak sesuai, dan tambahkan konten ensiklopedis yang ditulis dari sudut pandang net...

Mikhail KhodorkovskyKhodorkovsky pada tahun 2013 setelah dibebaskan dari penjaraLahirMikhail Borisovich Khodorkovsky26 Juni 1963 (umur 60)Moskow, Uni SovietKebangsaanRusiaAlmamaterMendeleev Russian University of Chemistry and TechnologyPekerjaanKepala Group Menatep (1990-)Wakil Menteri Bahan Bakar dan Energi Rusia (1993) Pimpinan dan CEO Yukos (1997–2004)Kolumnis The New Times (2011-)Suami/istriElena Dobrovolskaya (cerai) Inna KhodorkovskayaAnak4 Mikhail Borisovich Khodorkovsky (bahas...

Mamma Mia!Meryl Streep e Pierce Brosnan in una scena del filmLingua originaleinglese Paese di produzioneStati Uniti d'America, Regno Unito, Germania Anno2008 Durata108 min Rapporto2,35 : 1 Generecommedia, sentimentale, musicale RegiaPhyllida Lloyd SceneggiaturaCatherine Johnson ProduttoreJudy Craymer, Gary Goetzman Produttore esecutivoBenny Andersson, Björn Ulvaeus, Tom Hanks, Rita Wilson, Mark Huffam Casa di produzioneUniversal Pictures, Relativity Media, Playtone, Litt...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

Moldovan surgeon and politician This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Nicolae Testemițanu – news · newspapers · books · scholar · JSTOR (December 2021) (Learn how and when to remove this message) Nicolae TestemițanuOR2002 stampMinister of Health of the Moldavian SSRIn office4 April 1963 –&...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Climax of the Cuban Revolution This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Battle of Santa Clara – news · newspapers · books · scholar · JSTOR (July 2022) (Learn how and when to remove this message) For the 1847 battle in California, see Battle of Santa Clara (1847). For the 1927 battle in Nicaragua, see...

The RecordNama lainHangul찍히면 죽는다 Alih Aksara yang DisempurnakanJjikhimyeon jukneundaMcCune–ReischauerTchikhimyŏn chuknŭnda SutradaraKim Ki-hunProduserPark Il-seo[1]Skenario Choo Ki-suck Han Chang-hak[1] Pemeran Kang Seong-min Park Eun-hye Penata musik Lee Sang-yong Lee Jong-gyo[1] SinematograferChung Chung-hoon[1]PenyuntingKyung Min-ho[1]PerusahaanproduksiSam Woo Communications[1]Tanggal rilis 26 Agustus 2000 (20...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bread Givers – news · newspapers · books · scholar · JSTOR (May 2008) (Learn how and when to remove this message) First US edition(publ. Doubleday, Page) Bread Givers is a 1925 three-volume novel by Jewish-American author Anzia Yezierska; the story of a young g...

Lord Speaker of the House of Lords The Right HonourableThe Lord McFall of AlcluithPCOfficial portrait, 2022Lord Speaker of the House of LordsIncumbentAssumed office 1 May 2021Monarchs Elizabeth II Charles III DeputyThe Lord Gardiner of KimblePreceded byThe Lord FowlerSenior Deputy Speaker of the House of LordsIn office1 September 2016 – 30 April 2021Lord SpeakerThe Lord FowlerPreceded byThe Lord Laming (as Chairman of Committees)Succeeded byThe Lord Gardiner of KimbleChairman o...

Species of rodent Mindanao lowland forest mouse Conservation status Data Deficient (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Rodentia Family: Muridae Genus: Apomys Species: A. littoralis Binomial name Apomys littoralis(Sanborn, 1952) The Mindanao lowland forest mouse (Apomys littoralis) is a species of rodent in the family Muridae. It is found only in the Philippines. References ^ Kennerley, R. (2016)...

Nikki HahnHahn, 2011LahirSofia Nicole Hahn[1]13 November 2002 (umur 21)San Antonio, Texas, A.S.PekerjaanAktrisTahun aktif2009–sekarang Sofia Nicole Hahn[1] (lahir 13 November 2002)[2] adalah seorang aktris Amerika dan mantan aktris cilik. Dia dikenal karena perannya sebagai Emily Cooper di Adventures in Babysitting, serta peran di televisi lainnya. Referensi ^ a b Nikki Hahn. ^ Happy Birthday Nikki. Nikkihahn.com (Nikki Hahn • The Official Site). N...
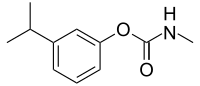
m-Cumenyl methylcarbamate Names Preferred IUPAC name 3-(Propan-2-yl)phenyl methylcarbamate Other names 3-Isopropylphenyl N-methylcarbamate; 3-Isopropylphenyl methylcarbamate; m-Cumenol methylcarbamate; m-Cumenyl methylcarbamate; m-Isopropylphenol methylcarbamate; m-Isopropylphenyl N-methylcarbamate; m-Isopropylphenyl methylcarbamate Identifiers CAS Number 64-00-6 Y 3D model (JSmol) Interactive image ChemSpider 5913 ECHA InfoCard 100.000.521 PubChem CID 6143 UNII 27502G8UZX Y CompTo...

Angkor Airways IATA ICAO Kode panggil G6 AKW ANGKORWAYS Didirikan2004Berhenti beroperasi2008Armada2Tujuan7SloganBring the World to Angkor WatKantor pusatPhnom Penh, KambojaSitus webhttp://www.angkorairways.com/ Angkor Airways MD-83 Angkor Airways Corporation adalah maskapai penerbangan yang pernah beroperasi di Phnom Penh, Kamboja. Maskapai penerbangan ini memulai layanan pada tahun 2004 dan telah secara substansial diinvestasikan oleh perusahaan asal Taiwan, Far Eastern Air Transport (FAT) s...

Кассіні — ГюйгенсКассіні — ГюйгенсОсновні параметриПовна назваКассіні — ГюйгенсCOSPAR ID1997-061ANORAD ID25008Організація НАСА, ЄКА, ІКА.ВиготівникЛРРОператорНАСА, ЛРРТип апаратадослідження Сатурна та його супутників, приземлення на Титан.Вихід на орбіту1 липня 2004Дата запуску15 ж...

1. Division 1975-1976 Competizione Fußball-Bundesliga Sport Calcio Edizione 65ª Organizzatore ÖFB Luogo Austria Partecipanti 10 Cronologia della competizione 1974-75 1976-77 Manuale L'edizione 1975-76 della Bundesliga vide la vittoria finale dell'Austria Vienna. Capocannoniere del torneo fu Hans Pirkner dell'Austria Vienna con 21 reti. Classifica finale Classifica G V N P GF GS Pt 1 Austria Vienna 36 21 10 5 77 29 52 2 FC Wacker Innsbruck 36 18 9 9 68 38 45 3 Rapid Vienna 36 17 6 13...

Vindiciae contra tyrannosVindiciae contra tyrannos (meaning: Defences [of liberty] against tyrants[1]) was an influential Huguenot tract published in Basel in 1579. Its author remains uncertain, since it was written under the pseudonym of Stephen Junius Brutus.[1] Likely candidates for its authorship include Hubert Languet and Philippe de Mornay.[2][3] In 1931, Gerardina Tjaberta van Ysselsteyn conjectured that the tract was a collaboration between Languet and...

30–375 AD empire in Central and South Asia Kushan Empireकुषाणसाम्राज्यम् (Sanskrit)Κοϸανο (Bactrian)Βασιλεία Κοσσανῶν (Ancient Greek)30–375A map of India in the 2nd century AD showing the extent of the Kushan Empire (in green) during the reign of Kanishka. Most historians consider the empire to have variously extended as far east as the middle Ganges plain,[1] to Varanasi in the eastern Gangetic plain,[2]...