Read other articles:

Historic fortress off the coast of Veracruz, Mexico This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: San Juan de Ulúa – news · newspapers · books · scholar · JSTOR (February 2021) (Learn how and when to remove this template message) 19°12′33″N 96°07′53″W / 19.20917°N 96.13139°W&#x...

Japanese visual novel, game, and anime series Meiji Tokyo RenkaAnime key visual明治東亰恋伽(Meiji Tōkyō Renka)GenreReverse harem[1] Light novelWritten byYukiko UozumiIllustrated byKaruPublished byKadokawa ShotenImprintKadokawa Beans BunkoDemographicFemaleOriginal runJune 30, 2012 – March 30, 2013Volumes2 (List of volumes) GameDeveloperBroccoliPublisherBroccoliGenreVisual novelPlatformPlayStation PortableReleasedJP: September 26, 2013 GameMeiji Tokyo Renka: Twi...

Jacques Le Lieur Jacques Le Lieur devant les conseillers de la ville de Rouen (1526). Données clés Naissance vers 1480 France Décès vers 1550 France Nationalité  Royaume de France Pays de résidence France Profession secrétaire et notaire du roi Activité principale conseiller-échevin de Rouen Autres activités sieur de Bresmetot et du Bosc-Bénard-Commin Ascendants Jacques Le Lieur, maire de RouenVincent Le Lieur, abbé de Saint-Pierre de Préaux Conjoint Jehanne Osmont Descenda...

The Gurkha MuseumPeninsula BarracksShown in HampshireEstablished1974LocationPeninsula Barracks, Winchester, United KingdomCoordinates51°03′45″N 1°19′13″W / 51.0624°N 1.3203°W / 51.0624; -1.3203TypeMilitaryWebsitewww.thegurkhamuseum.co.uk The Gurkha Museum commemorates the service of Gurkha soldiers to the British Crown, a relationship that has endured since 1815. It is located in Winchester in Hampshire, England and is part of Winchester's Military Museums...

Open cluster in the constellation Cassiopeia NGC 129DSS image of NGC 129Observation data (J2000 epoch)Right ascension00h 30m 00s[1]Declination+60° 13′ 06″[1]Distance5,450 ly (1,670 pc[2])Apparent magnitude (V)6.5 [1]Apparent dimensions (V)21'Physical characteristicsEstimated age76 millions years[2]Other designationsCollinder 2AssociationsConstellationCassiopeiaSee also: Open cluster, List of open clusters N...

American diplomat (1903–1987) Carlyle Elwood Maw (October 13, 1903 – December 1, 1987) was Under Secretary of State for International Security Affairs from July 10, 1974, to September 17, 1976. Born in Provo, Utah, he graduated from Brigham Young University and from Harvard Law School. He had been an attorney in New York City when he went to work for Henry Kissinger as a legal advisor. He was appointed on November 23, 1973, and held this post from November 27, 1973, to July 9, 1974. Later...

豪栄道 豪太郎 場所入りする豪栄道基礎情報四股名 澤井 豪太郎→豪栄道 豪太郎本名 澤井 豪太郎愛称 ゴウタロウ、豪ちゃん、GAD[1][2]生年月日 (1986-04-06) 1986年4月6日（38歳）出身 大阪府寝屋川市身長 183cm体重 160kgBMI 47.26所属部屋 境川部屋得意技 右四つ・出し投げ・切り返し・外掛け・首投げ・右下手投げ成績現在の番付 引退最高位 東大関生涯戦歴 696勝493敗...

British-bred Thoroughbred racehorse MemoirMemoir in the Welbeck Stud, c. 1897.SireSt SimonGrandsireGalopinDamQuiverDamsireToxophiliteSexMareFoaled1887[1]CountryUnited KingdomColourBrownBreederNational StudOwnerWilliam Cavendish-Bentinck, 6th Duke of PortlandTrainerGeorge DawsonRecord21: 8-3-0Earnings£17,010Major winsPrendergast Stakes (1889)Newmarket Stakes (1890)Oaks Stakes (1890)Nassau Stakes (1890)St Leger (1890)Newmarket Oaks (1890)July Cup (1891) Memoir (1887 – 1908) was a...

Alcuni oggetti studiati in analisi matematica Funzioni Limiti Derivate Integrali Equazioni differenziali Funzioni a più variabili Funzioni complesse Campi vettoriali L'analisi matematica è il campo della matematica che si occupa delle proprietà che emergono dalla scomposizione infinita di un insieme denso. Si fonda sul calcolo infinitesimale, con il quale, attraverso le nozioni di limite e continuità, studia il comportamento locale di una funzione utilizzando gli strumenti del calcol...

Establishment of racial discrimination as a policy within a society or organisation Not to be confused with Societal racism, Structural inequality, Structural violence, or Structural abuse. Institutional racism, also known as systemic racism, is defined as policies and practices that exist throughout a whole society or organization that result in and support a continued unfair advantage to some people and unfair or harmful treatment of others based on race or ethnic group. It manifests as dis...

American trade group This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (September 2021) Edison Electric InstituteFormation1933Headquarters701 Pennsylvania Avenue, N.W. Washington, D.C. 20004-2696Location38°53′39.9″N 77°1′20.4″W / 38.894417°N 77.022333°W / 38.894417; -77.022333ChairmanPedro J. PizarroPresidentDan Br...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Kabupaten Sukabumi – berita · surat kabar · buku · cendekiawan · JSTOR (Agustus 2022) Halaman ini berisi artikel tentang kabupaten. Untuk kota bernama sama, lihat Kota Sukabumi. Untuk kegunaan lain, lihat Suk...

Town and civil parish in Northumberland, England Human settlement in EnglandBerwick-upon-TweedBerwick-upon-Tweed behind its defensive wallsBerwick-upon-TweedLocation within NorthumberlandPopulation12,043 (2011 Census)OS grid referenceNT995525• London304 mi (489 km)Civil parishBerwick-upon-TweedUnitary authorityNorthumberlandCeremonial countyNorthumberlandRegionNorth EastCountryEnglandSovereign stateUnited KingdomPost townBERWICK-UPON-TWEEDPostcod...

南巴西镇Sul Brasil市镇南巴西镇在巴西的位置坐标：26°44′09″S 52°57′54″W / 26.7358°S 52.965°W / -26.7358; -52.965国家巴西州圣卡塔琳娜州面积 • 总计114.9 平方公里（44.4 平方英里）海拔418 公尺（1,371 英尺）人口（2007） • 總計3,061人 • 密度26.6人/平方公里（69人/平方英里） 南巴西镇（葡萄牙语：Sul Brasil）是巴西圣卡塔琳�...

此條目没有列出任何参考或来源。 (2018年8月4日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 鄧陳常（越南语：Đặng Trần Thường／鄧陳常，1759年—1813年），越南阮朝將領、官員。開國功臣。 鄧陳常是河內彰德縣（今彰美縣）人，出生在後黎朝末期。後黎朝滅亡後，西山朝曾請他當官，但他卻�...

Pour les articles homonymes, voir Swiss. Swiss Olympic Sport(s) représenté(s) Omnisports Création 1912 Président Jürg Stahl Siège Ittigen près de Berne Affiliation Comités olympiques européens Site internet Site officiel de Swiss Olympic modifier  La Maison du Sport, le siège de Swiss Olympic Swiss Olympic (également dénommée Association Olympique Suisse, Schweizerischer Olympischer Verband et Associazione Olimpica Svizzera) est à la fois le Comité national olympique suis...

1895 1900 Élections législatives italiennes de 1897 508 sièges à la Chambre des députés 21 mars - 28 mars 1897 Corps électoral et résultats Inscrits 2 120 909 Votants 1 241 486   58,54 %  0,7 Votes blancs 41 911 Gauche historique – Giovanni Giolitti Voix 799 517 64,37 %   5,8 Sièges obtenus 327  7 Droite historique – Antonio di Rudinì Voix 242 090 19,49 %   2,1 Sièges ...

Phenomenon in maths Rotation number for different values of two parameters of the circle map: Ω on the x-axis and K on the y-axis. Some tongue shapes are visible. In mathematics, particularly in dynamical systems, Arnold tongues (named after Vladimir Arnold)[1][2] are a pictorial phenomenon that occur when visualizing how the rotation number of a dynamical system, or other related invariant property thereof, changes according to two or more of its parameters. The regions of c...

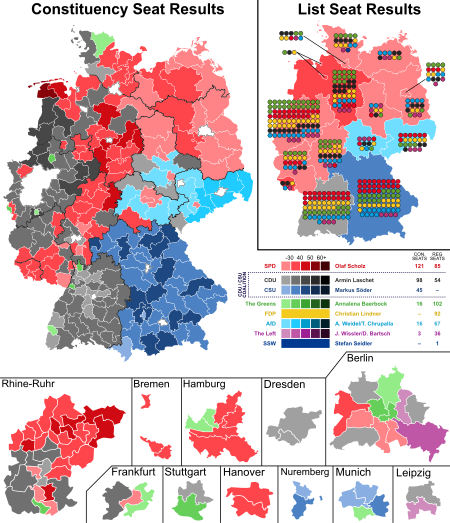
Main article: 2021 German federal election 2021 German federal election ← 2017 26 September 2021 Next → All 736 seats in the Bundestag368 seats needed for a majorityTurnout76.6% 0.4pp Party Leader Vote % Seats +/– SPD Olaf Scholz 25.7% 206 +53 CDU/CSU Armin Laschet 24.1% 197 −49 Greens Annalena Baerbock 14.7% 118 +51 FDP Christian Lindner 11.4% 91 +11 AfD A. Weidel/T. Chrupalla 10.4% 83 −11 Left J. Wissler/D. Bartsch 4.9% 39 −30 SSW Stefan Seidler 0.1% 1 +1 ...

Set of musical pitches The Quadrangularis Reversum, an instrument constructed by Harry Partch based on the 11-limit tonality diamond In music theory and tuning, a tonality diamond is a two-dimensional diagram of ratios in which one dimension is the Otonality and one the Utonality.[1] Thus the n-limit tonality diamond (limit here is in the sense of odd limit, not prime limit) is an arrangement in diamond-shape of the set of rational numbers r, 1 ≤ r < 2 {\displaystyle 1\leq r...