Read other articles:

Borneo Airways Limited IATA ICAO Kode panggil AB Didirikan1957Berhenti beroperasi1965 (diakuisisi Malaysian Airways dan menjadi Malaysia-Singapore Airlines) Borneo Airways adalah nama dua bekas maskapai penerbangan. Maskapai pertama, Borneo Airways Limited, berpangkalan di Borneo Britania (sekarang negara bagian Sabah dan Sarawak, Malaysia, dan Brunei Darussalam) dan beroperasi tahun 1950-an sampai 1965. Borneo AIrways beroperasi tahun 1997–1999 di Brunei. Sejarah Borneo Airways Limited (19...

Early Christian governance councils Icon depicting the Emperor Constantine (centre), accompanied by the bishops of the First Council of Nicaea (325), holding the Niceno–Constantinopolitan Creed of 381 In the history of Christianity, the first seven ecumenical councils include the following: the First Council of Nicaea in 325, the First Council of Constantinople in 381, the Council of Ephesus in 431, the Council of Chalcedon in 451, the Second Council of Constantinople in 553, the Third Coun...

Questa voce o sezione sull'argomento calciatori australiani non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: per le nazionali giovanili Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce sull'argomento calciatori australiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti d...

Pour les articles homonymes, voir Dormann. Maurice Dormann Maurice Dormann en 1929. Fonctions Député de Seine-et-Oise 1928 – 1936(8 ans) Groupe politique GR (1928-1932)IDG (1932-1936)NI (1936-1940) Ministre des Pensions 23 décembre 1930 – 27 janvier 1931(1 mois et 4 jours) Gouvernement Steeg Sénateur de Seine-et-Oise 1936 – 1940(4 ans) Biographie Date de naissance 20 avril 1881 Date de décès 17 décembre 1947 (à 66 ans) Lieu de décès 16e arrondiss...

MućcomuneLocalizzazioneStato Croazia Regione Spalatino-dalmata TerritorioCoordinate43°43′34″N 16°30′00″E / 43.726111°N 16.5°E43.726111; 16.5 (Muć)Coordinate: 43°43′34″N 16°30′00″E / 43.726111°N 16.5°E43.726111; 16.5 (Muć) Superficie210,80 km² Abitanti3 882[2] (2011) Densità18,42 ab./km² Altre informazioniCod. postale21255 Prefisso021 Fuso orarioUTC+1 CartografiaMuć Sito istituzionaleModifica dati su...

سيزيريات    شعار الاسم الرسمي (بالفرنسية: Ceyzériat)‏  الإحداثيات 46°10′42″N 5°19′26″E / 46.178333333333°N 5.3238888888889°E / 46.178333333333; 5.3238888888889 [1]  [2] تقسيم إداري  البلد فرنسا[3]  التقسيم الأعلى آن  خصائص جغرافية  المساحة 9.36 كيلومتر مربع[1]  عدد ال...

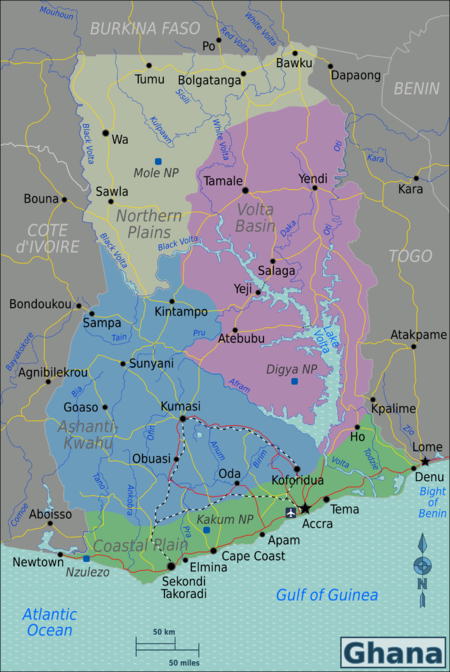
Divisions of Ghana Politics of Ghana Constitution Executive President (list) Nana Akufo-Addo Vice President Mahamudu Bawumia Ministers Council of State Legislative Speaker of the Parliament Alban Sumana Bagbin Parliament Members of Parliament Judiciary Supreme Court Chief Justice: Kwasi Anin-Yeboah Human rights Elections Constituencies Political parties Politicians Electoral Commission Recent elections General: 201620202024 Administrative divisions Regions Districts Foreign relations Ministry...

Place in East Region, SingaporeSiglapSubzone of Bedok Planning Area & Housing EstateOther transcription(s) • MalaySiglap (Rumi)سيݢلڤ‎ (Jawi) • Chinese实乞纳 (Simplified)實乞納 (Traditional)Shíqǐnà (Pinyin)Si̍t-khit-la̍p (Hokkien POJ) • Tamilசிக்லாப்Ciklāp (Transliteration)John Edmund Taylor, View along the Beach by Singlap, Singapore (1879)Country SingaporeRegionEast Region Siglap Districts Map Comparison...

Computer networking technique This article is about one-to-many communications in computer networks. For radio systems, see Point-to-multipoint communication. For broadcasting multiple programs using a single channel, see Multicast channel. Routing schemes Unicast Broadcast Multicast Anycast In computer networking, multicast is a type of group communication where data transmission is addressed to a group of destination computers simultaneously.[1] Multicast can be one-to-many or many-...

Active galaxy in the constellation Hercules Not to be confused with Hercules (dwarf galaxy). Hercules AVisible light image obtained by Hubble superposed with a radio image taken by the VLA.Observation data (J2000 epoch)ConstellationHerculesRight ascension16h 51m 08.15sDeclination+04° 59′ 33.32″Distance2.1 Gly (643.9 Mpc)CharacteristicsTypecD; E3Other designationsHerc A, 3C 348 Hercules A is a bright astronomical radio source in the constellation Hercules[1] ...

Our Lady of Guadalupe Church & International Shrine of St. Jude is a Roman Catholic church located on Rampart Street in New Orleans, Louisiana. It is the oldest surviving church building in the city (originally established as the Chapel of St. Anthony of Padua), the back of the church is bordered by Basin Street, and the parish is predominantly African-American. The church is one of multiple parishes in the city that celebrates a weekly Gospel Jazz Mass on Sunday mornings. Exterior of Our...

  لمعانٍ أخرى، طالع وزارة المالية (توضيح). وزارة المالية (سنغافورة) وزارة المالية (سنغافورة)   تفاصيل الوكالة الحكومية البلد سنغافورة  الموظفون 1523   الإدارة منصب المدير وزير المالية  [لغات أخرى]‏  الوزراء المسؤولون لورانس وونغ موقع الويب الموقع الرسمي&...

Method in number theory Elwyn R. Berlekamp at conference on Combinatorial Game Theory at Banff International Research Station Elwyn Berlekamp In number theory, Berlekamp's root finding algorithm, also called the Berlekamp–Rabin algorithm, is the probabilistic method of finding roots of polynomials over the field F p {\displaystyle \mathbb {F} _{p}} with p {\displaystyle p} elements. The method was discovered by Elwyn Berlekamp in 1970[1] as an auxiliary to the algorithm for polynomi...

Just for One Day (song) redirects here. For the song by The Grace, see Graceful 4. 2003 single by David Guetta vs. BowieJust for One Day (Heroes)Single by David Guetta vs. Bowiefrom the album Fuck Me I'm Famous 2003 Released16 June 2003Recorded2003GenreHousepop rockLength3:00LabelVirginSongwriter(s)David BowieProducer(s)David GuettaJoachim GarraudDavid Guetta singles chronology Give Me Something (2002) Just for One Day (Heroes) (2003) Money (2004) Just for One Day (Heroes) is a house song...

Marine scientist Susanne Menden-DeuerAlma materUniversity of WashingtonUniversity of BonnOccupation(s)Oceanographer and marine scientistScientific careerInstitutionsUniversity of Rhode IslandThesisLinking individual foraging strategies with ecological dynamics : quantifying zooplankton movements in heterogeneous resource distributions (2004) Susanne Menden-Deuer is an oceanographer and marine scientist known for her work on marine food webs, including their structure and functi...

Der Gläserne Bär ist ein Kinder- und Jugendfilmpreis, der seit 1994 jährlich bei den Berliner Filmfestspielen von einer Kinder- und einer Jugendjury vergeben wird. Vorläufer war von 1986 bis 1993 der Preis der Kinderjury, den zunächst jährlich nur ein Film erhielt. Ab 1992 wurden jeweils ein Spielfilm und ein Kurzfilm für diesen Preis ausgewählt. 1994 erfolgte in Analogie zu den übrigen Preisen der Berlinale die Umbenennung des Preises in Gläserner Bär. 2004 wurden für jedes Jahr ...

Multiple comic book series Amazing Adventures is the name of several anthology comic book series, all but one published by Marvel Comics. The earliest Marvel series of that name introduced the company's first superhero of the late-1950s to early-1960s period fans and historians call the Silver Age of Comic Books. That same series also included the first comic book to be labeled Marvel Comics. Ziff-Davis The first series titled Amazing Adventures was a 1950s science fiction anthology produced ...

Heraldic charge A cross fleury A cross fleury (or flory) is a cross adorned at the ends with flowers in heraldry.[1] It generally contains the fleur-de-lis, trefoils, etc. Synonyms or minor variants include fleuretty, fleuronny, floriated and flourished.[2] In early armory, it is not consistently distinguished from the cross patonce.[3] See also Charge (heraldry) Cross References ^ Newton, William (1846). A Display of Heraldry. William Pickering. p. 165. Retrieved...

البترون تقسيم إداري البلد  لبنان[1][2] عاصمة لـ قضاء البترون  التقسيم الأعلى لبنان  خصائص جغرافية إحداثيات 34°15′N 35°39′E / 34.25°N 35.65°E / 34.25; 35.65 المساحة 4.68 كيلومتر مربع  الارتفاع 34 السكان التعداد السكاني 45,000 نسمة (إحصاء ) الكثافة السكانية auto معلومات...

«Malaya» redirige aquí. Para otras acepciones, véase montañas Malaya. Para otros usos de este término, véase Malaca (desambiguación). Península de Malaca Semenanjung Tanah Melayu UbicaciónContinente Sudeste asiáticoMar Mar de Andamán, Mar de China Meridional y golfo de TailandiaEstrecho Estrecho de Malaca y estrecho de JohorPaís Birmania Birmania Malasia MalasiaSingapur Singapur TailandiaCoordenadas 7°N 100°E / 7, 100CaracterísticasTipo Pen�...