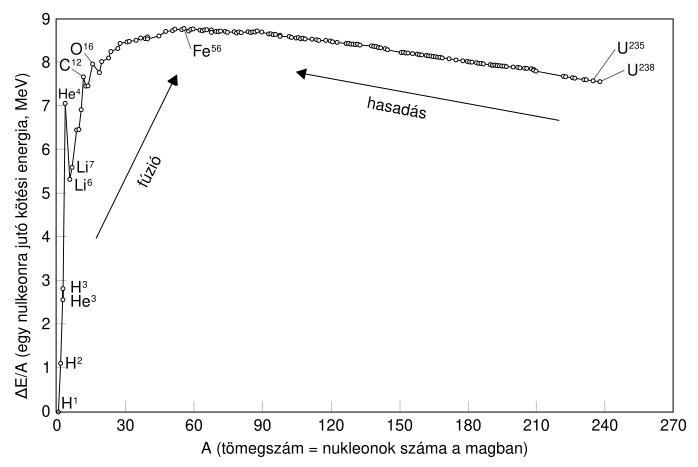
Kötési energia
|
Read other articles:

Dian Triansyah Djani Presiden Dewan Keamanan Perserikatan Bangsa-BangsaPeriode Keanggotaan: 2019—2020Masa jabatan1 Agustus 2020 – 31 Agustus 2020Sekretaris JenderalAntónio Guterres PendahuluChristoph HeusgenPenggantiAbdou AbarryMasa jabatan1 Mei 2019 – 31 Mei 2019Menjabat bersama Retno MarsudiSekretaris JenderalAntónio Guterres PendahuluChristoph HeusgenPenggantiMansour Al-OtaibiUtusan Tetap Indonesia untuk Perserikatan Bangsa-Bangsa ke-19Masa jabatan12 A...

Questa voce o sezione sull'argomento edizioni di competizioni calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Serie C2 1984-1985 Competizione Serie C2 Sport Calcio Edizione 7ª Organizzatore Lega Nazionale Serie C Date dal 23 settembre 1984al 27 giugno 1985 Luogo Italia Partecipanti 72...

Artikel ini bukan mengenai Stasiun Sukaraja. Stasiun Sokaraja Sokaraja+96 m Fasad stasiun Sokaraja, Mei 2022LokasiJalan Amad IISokaraja Kidul, Sokaraja, Banyumas, Jawa TengahIndonesiaKoordinat{{WikidataCoord}} – missing coordinate dataKetinggian+96 mOperator Kereta Api IndonesiaDaerah Operasi V Purwokerto Letakkm 37+578 lintas Maos-Purwokerto Timur-Banjarnegara-Wonosobo[1] Layanan-KonstruksiJenis strukturAtas tanahInformasi lainKode stasiun SOK 2229[2] KlasifikasiIII/kecil&#...

Tour cycliste international de la Guadeloupe 2017 GénéralitésCourse67e Tour cycliste international de la GuadeloupeCompétitionUCI Europe Tour 2017Étapes12Dates28 juillet – 6 août 2017Distance1 267,59 kmPays FranceLieu de départPointe-à-PitreLieu d'arrivéeBaie-MahaultPartants141Arrivants88Vitesse moyenne40,684 km/hSite officielSite officielRésultatsVainqueur Sébastien Fournet-Fayard (Pro Immo Nicolas Roux)Deuxième Juan MurilloTroisième Žydrūnas Savickas (Bourg-en-Bresse A...

Bandar Udara Internasional Sam Ratulangi ManadoSam Ratulangi International Airport ManadoIATA: MDCICAO: WAMMWMO: 97014InformasiJenisSipil / MiliterPemilikPT Aviasi Pariwisata Indonesia (Persero)PengelolaAngkasa Pura IMelayaniBimindoLokasiManado, Sulawesi Utara, IndonesiaMaskapai utama Citilink Garuda Indonesia Lion Air Wings Air Ketinggian dpl81 mdplKoordinat01°32′57″N 124°55′35″E / 1.54917°N 124.92639°E / 1.54917; 124.92639Koordinat: 01°32′57�...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

هذه المقالة عن محمد بن جرير الطبري. لمعانٍ أخرى، طالع الطبري (توضيح). الإمام محمد الطبري أَبُو جَعْفَر مُحَمَّد بْن جَرِير بْن يَزِيد ٱلطَّبَرِيّ معلومات شخصية الميلاد سنة 839 [1][2][3] آمل الوفاة سنة 923 (83–84 سنة)[4][1][3] بغداد مكا�...

Краснофигурная пелика вазописца Полигнота. Юноша рассчитывается с гетерой. Ок. 430 г. до н. э. Проституция являлась частью повседневной жизни древних греков архаического периода. В крупнейших греческих городах и особенно в портах в ней была занята значительная час...

لمعانٍ أخرى، طالع إرث (توضيح). الإرث (وقد يرادفه الميراث فهو تركة الميت) هي عادة توريث ممتلكات أو ألقاب أو ديون أو مسؤوليات عند وفاة أحد الأشخاص. وهي من العادات الأساسية في المجتمعات. وقوانين الميراث يختلف من مجتمع إلى آخر وما بين الأديان وكما أنه تطور عبر الأزمان ، مما...

Department of Guatemala You can help expand this article with text translated from the corresponding article in Spanish. (January 2023) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that ...

Commune and town in Ouargla Province, AlgeriaAin Beida ﻋﻴﻦ اﻟﺒﻴﻀﺎءCommune and townLocation of Ain Beida commune within Ouargla ProvinceAin BeidaLocation of Ain Beida within AlgeriaCoordinates: 31°56′18″N 5°24′1″E / 31.93833°N 5.40028°E / 31.93833; 5.40028Country AlgeriaProvinceOuargla ProvinceDistrictSidi Khouïled DistrictArea[1] • Total1,973 km2 (762 sq mi)Elevation139 m (456 ft)Populatio...

Federal court for Alaska, United States United States District Court for the District of Alaska(D. Alaska)LocationAnchorageMore locationsFairbanksHurff Ackerman Saunders Federal Building and Robert Boochever U.S. Courthouse(Juneau)Appeals toNinth CircuitEstablishedJanuary 3, 1959Judges3Chief JudgeSharon L. GleasonOfficers of the courtU.S. AttorneyS. Lane TuckerU.S. MarshalRobert Heunwww.akd.uscourts.gov The United States District Court for the District of Alaska (in case c...

Coin-shaped post-fermented tea This article is about Korean tea. For a song, see Doncha? DonchaTypePost-fermented teaOther names Cheongtae-jeon jeoncha OriginKoreaQuick descriptionCoin-shaped post-fermented teaTemperature85–95 °C (185–203 °F)Time5‒10 minutes Korean nameHangul돈차Hanja돈茶Revised RomanizationdonchaMcCune–Reischauertonch'aIPA[ton.tɕʰa]Alternative nameHangul전차Hanja錢茶Revised RomanizationjeonchaMcCune–Reischauerchŏnch'aIPA[tɕʌn.t�...

本模板依照頁面品質評定標準无需评级。本Template属于下列维基专题范畴: 大学专题 (获评模板級、不适用重要度) 大学PJ:大学Template:大学专题大学条目 大学主题查论编本Template属于大学专题范畴,该专题旨在改善中文维基百科大学类内容。如果您有意参与,请浏览专题主页、参与讨论,并完成相应的开放性任务。 模板 根据专题质量评级标准,本Template�...

Lukisan potret Jeong Seon Jeong Seon (1676-1759) adalah pelukis dari Dinasti Joseon, Korea.[1] Berasal dari golongan bangsawan, Jeong Seon merupakan pelukis yang berani mendobrak kebiasaan awam para pelukis Korea pada abad ke-17. Sampai di akhir abad ke-17, sebagian besar pelukis Korea sangat dipengaruhi oleh gaya lukisan Cina yang terlalu mengagung-agungkan pemandangan alam. Jeong Seon berkelana ke seluruh Korea untuk mencari ilham serta mempelajari alam di sekitarnya.[1] Gay...

El Salvador Kapitän Miguel Merz Aktuelles ITF-Ranking 52 Statistik Erste Teilnahme 1991 Davis-Cup-Teilnahmen 26 Bestes Ergebnis Amerika Gruppenzone II(11 Teilnahmen) Ewige Bilanz 53:37 Erfolgreichste Spieler Meiste Siege gesamt Rafael Arévalo (52) Meiste Einzelsiege Rafael Arévalo (31) Meiste Doppelsiege Rafael Arévalo (21) Bestes Doppel Rafael Arévalo / Marcelo Arévalo (12) Meiste Teilnahmen Manuel-Antonio Tejada-Ruiz (45) Meiste Jahre Rafael Arévalo (14) Letzte Aktualisierung der In...

In Greek mythology, Amphiclus (Ancient Greek: Ἄμφικλον or Ἄμφικλος) may refer to two different characters: Amphiclus, succeeded King Oenopion and his sons on the throne of Chios. He came from Histiaea in Euboea and went to the island of Chios because of an oracle from Delphi.[1] Amphiclus, a Trojan soldier who participated in the Trojan War and was slain by Meges, one of the Achaean Leaders.[2] References ^ Pausanias, 7.4.9 ^ Homer, Iliad 16.313 This article ...

Voce principale: Associazione Sportiva Dilettantistica Fidelis Andria 1928. Associazione Sportiva Fidelis AndriaStagione 1995-1996Sport calcio Squadra Fidelis Andria Allenatore Giuliano Sonzogni (1ª-36ª) Stefano Boggia (37ª-38ª) Presidente Giuseppe Fuzio Serie B17º posto. Retrocessa in Serie C1 Coppa ItaliaPrimo turno Maggiori presenzeCampionato: M. Giampaolo e Masolini (36) Miglior marcatoreCampionato: Masolini (7) StadioStadio degli Ulivi 1994-1995 1996-1997 Si invita a seguire i...

笠置山の戦い 笠置山の戦いを再現した人形。弓で戦う武将は足助重範。巨岩を敵に投げつけようとしているのは般若寺の僧本性房。(京都府相楽郡笠置町) 戦争:元弘の乱 年月日:(旧暦)元弘元年9月2日 - 同年9月28日(ユリウス暦)1331年10月4日 - 同年10月30日 場所:山城国相楽郡笠置山 結果:笠置山陥落 交戦勢力 後醍醐天皇勢力 鎌倉幕府 指導者・指揮官 千種忠�...