Kitérés
|
Read other articles:

Cerbera odollam Cerbera odollam, atau pohon pong-pongStatus konservasiRisiko rendahIUCN61984781 TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmesangiospermsKladeudicotsKladcore eudicotsKladasteridsKladlamiidsOrdoGentianalesFamiliApocynaceaeSubfamiliRauvolfioideaeTribusPlumerieaeSubtribusThevetiinaeGenusCerberaSpesiesCerbera odollam Gaertn. lbs Cerbera odollam, pohon pong-pong adalah sebuah spesies tumbuhan angiospermae dicotyledonous dalam keluarga Apocynaceae dan umum...

Pour les articles homonymes, voir Mettler. MettlerGéographiePays États-UnisÉtat CalifornieComté comté de KernSuperficie 0,6 km2 (2010)Surface en eau 0 %Altitude 165 mCoordonnées 35° 03′ 45″ N, 118° 58′ 18″ ODémographiePopulation 90 hab. (2020)Densité 150 hab./km2 (2020)FonctionnementStatut Localité de recensement aux États-UnisIdentifiantsCode postal 93381Code FIPS 06-47164GNIS 245837, 2408825Indicatif téléphonique 66...

Heart of Fire redirects here. For the Kentucky church, see Dan Johnson (Kentucky politician) § Heart of Fire Church. 2014 studio album by Black Veil BridesBlack Veil BridesStudio album by Black Veil BridesReleasedOctober 27, 2014 (2014-10-27)StudioSteakhouse Studios, North Hollywood, Los Angeles, CA Paradise Studios, Hollywood, CA The Warehouse, Vancouver, British Columbia, CanadaGenre Heavy metal[1] hard rock[1] metalcore[1] Length44:02(47...

Red Ronnie Red Ronnie, pseudonimo di Gabriele Ansaloni (San Pietro in Casale, 15 dicembre 1951[1][2]), è un giornalista, critico musicale, conduttore televisivo e conduttore radiofonico[1] italiano. Indice 1 Biografia 1.1 DJ radiofonico (1975-1979) 1.1.1 Attività giornalistica ed editoriale 1.2 Produttore discografico (1979-1989) 1.3 Attività in radio e televisione (1983-2001) 1.3.1 Candidato alle elezioni (1992) 1.4 Spettacoli e festival (2001-2006) 1.5 Consulente ...

Passenger train service in Bangladesh Panchagarh ExpressOverviewService typeIntercity trainCurrent operator(s)Bangladesh RailwayRouteTerminiKamalapur railway stationBir Muktijoddha Sirajul Islam Railway StationDistance travelled526 km (327 mi)Average journey time9 hoursService frequencyDailyTrain number(s)৭৯৩/৭৯৪On-board servicesClass(es)AC, Non-AC, ShovanSeating arrangementsYesSleeping arrangementsYesCatering facilitiesYesTechnicalRolling stock14Track gauge1,676 mm...

Abdul Qadir bin Abdul MuthalibNamaAbdul Qadir bin Abdul MuthalibNisbahal-Indunisi al-Mandili al-Makki asy-Syafi’iJabatanUlama, guru, Da'iKarya yang terkenalTuhfah al-Qari‘ al-Muslim fi al-Ahadits al-Muttafaq ‘Alaiha Bayn al-Imam al-Bukhari wa al-Imam Muslim,Al-Khazain As-Saniyyah,Syarh ‘Aqidah Thahawiyyah, Dipengaruhi oleh Imam Asy-Syafi'iImam Ath-ThahawiImam An-NawawiMuhammad Yasin Al-Fadani Syekh Haji Abdul Qadir bin Abdul Muthalib bin Hassan (Arab: الشَّيْخُ عَبْ...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article provides insufficient context for those unfamiliar with the subject. Please help improve the article by providing more context for the reader. (March 2018) (Learn how and when to remove this template message) The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notabilit...

Шалфей обыкновенный Научная классификация Домен:ЭукариотыЦарство:РастенияКлада:Цветковые растенияКлада:ЭвдикотыКлада:СуперастеридыКлада:АстеридыКлада:ЛамиидыПорядок:ЯсноткоцветныеСемейство:ЯснотковыеРод:ШалфейВид:Шалфей обыкновенный Международное научное наз...

Denomination of Judaism The interior of Congregation Emanu-El of New York, the largest Reform synagogue in the world. Part of a series onJudaism Movements Orthodox Haredi Hasidic Modern Conservative Conservadox Reform Karaite Reconstructionist Renewal Humanistic Haymanot Philosophy Principles of faith Kabbalah Messiah Ethics Chosenness God Names Musar movement Texts Tanakh Torah Nevi'im Ketuvim Ḥumash Siddur Piyutim Zohar Rabbinic Mishnah Talmud Midrash Tosefta Law M...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (February 2023) (Learn how and when to remove this message) This article needs additional citations for verific...

Indian cricketer (born 1993) In this Indian name, the name Ramaswamy Gopal is a patronymic, and the person should be referred to by the given name, Shreyas. Shreyas GopalGopal in a post-match presentation during 2019 IPLPersonal informationFull nameRamswamy Shreyas GopalBorn (1993-09-04) 4 September 1993 (age 30)Bangalore, Karnataka, IndiaBattingRight-handedBowlingRight-arm leg breakRoleAll-rounderDomestic team information YearsTeam2013/14–2022/23Karnataka2014–2017Mumbai Indians...

Former Swedish aerospace manufacturer Volvo AeroIndustryAerospaceFounded1930Defunct2012FateAcquired by GKNSuccessorGKN Aerospace Engine SystemsHeadquartersTrollhättan, SwedenNumber of locationsTrollhättan, Linköping, Kongsberg (Norway), Newington, Connecticut (US)ParentVolvo F-104 on display outside Volvo Aero Volvo RM6B Volvo Flygmotor RM8B Volvo Aero was a Swedish aircraft, guided missiles[1] and rocket engine[2][3] manufacturer. It became GKN Aerospace Engine Sys...

Religion in Bolivia (2020)[1] Roman Catholic (63.2%) Protestant (21.5%) Other Christians (2.0%) None (9.3%) Other religion (1.2%) No answer (0.6%) St. Lawrence's Cathedral in Santa Cruz Christianity is the predominant religion in Bolivia, with Roman Catholicism being its largest denomination. Before the arrival of Spanish missionaries, the people residing in the territory of modern day Bolivia practiced a variety of f...

Les oligarques russes (en russe : олигархи , romanisé : oligarkhi) sont des personnalités de premier plan du monde des affaires, en lien avec le pouvoir politique, des anciennes républiques soviétiques qui se sont rapidement enrichies dans les années 1990 via les privatisations qui ont suivi la dissolution de l'Union soviétique. Un terme associé et complémentaire, mais qui n'est pas réservé aux personnalités de premier plan, est celui de Нувори́ш qui vient...

Divingat the Games of the XV OlympiadVenueHelsinki Swimming StadiumDates27 July 1952 (1952-07-27) through 2 August 1952 (1952-08-02)No. of events4Competitors76 from 22 nations← 19481956 → Diving at the1952 Summer Olympics3 m springboardmenwomen10 m platformmenwomenvte At the 1952 Summer Olympics in Helsinki, four diving events were contested.[1] Medal summary The events are labelled as 3 metre springboard and 10 metre plat...

ويليام الكسندر سميث (بالإنجليزية: William Smith) معلومات شخصية الميلاد 19 يوليو 1904 جوهانسبرغ الوفاة 20 ديسمبر 1955 (51 سنة) جوهانسبرغ الجنسية جنوب إفريقيا الحياة العملية المهنة ملاكم[1] نوع الرياضة الملاكمة تعديل مصدري - تعديل ويليام الكسندر سم...

Harar Brewery's Hakim Stout Beer is the most popular industrial alcoholic beverage in Ethiopia with lager being the most consumed type of beer. In the rural sector, the home-brew talla or siwa is still dominant. History The first brewery in Ethiopia was established in 1922 by St. George Beer (named after the patron saint of Ethiopia). Brands like Meta and Bedele are also older in Ethiopia but have since been acquired by foreign companies and re-branded. Industry Ethiopia's beer industry has g...

عيسى بن يونس معلومات شخصية اسم الولادة عيسى بن يونس بن أبي إسحاق عمرو بن عبد الله الهمداني السبيعي الميلاد الكوفة تاريخ الوفاة سنة 803 اللقب أبو محمد الديانة الإسلام الحياة العملية المهنة مُحَدِّث تعديل مصدري - تعديل أبو محمد عيسى بن يونس بن أبي إسحاق عمرو بن عبد �...

859 siege by the Aghlabids against the Byzantine city of Enna Siege of EnnaPart of the Muslim conquest of SicilyCastle of EnnaDate24 January 859LocationEnnaResult Aghlabid victoryBelligerents Byzantine Empire AghlabidsCommanders and leaders Theodotus Al-Abbas bin FadhlStrength Unknown 2,000 cavalryCasualties and losses Unknown Unknown vteArab–Byzantine warsEarly conflicts Mu'tah Balqa Firaz Dathin The Levant Marj Rahit al-Qaryatayn Bosra Ajnadayn Yaqusa Marj al-Saffar Sanita-al-Uqab Damascu...

Seaside village in County Donegal, Ireland Village in Ulster, IrelandNarin An FhearthainnVillageNarin strandNarinLocation in IrelandCoordinates: 54°50′19″N 8°26′47″W / 54.838748°N 8.446482°W / 54.838748; -8.446482CountryIrelandProvinceUlsterCountyCounty DonegalTime zoneUTC+0 (WET) • Summer (DST)UTC-1 (IST (WEST))Irish Grid ReferenceG818944 Narin (Irish: An Fhearthainn),[1] also Naran, is a small seaside village and townland in the parish...

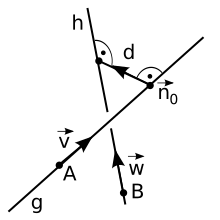











![{\displaystyle g:{\vec {x}}=\left({\begin{smallmatrix}a_{1}\\[0.7ex]a_{2}\\[0.7ex]a_{3}\end{smallmatrix}}\right)+r\left({\begin{smallmatrix}v_{1}\\[0.7ex]v_{2}\\[0.7ex]v_{3}\end{smallmatrix}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/addeafeab1494483166aec1a6166383aedcc1807)
![{\displaystyle h:{\vec {x}}=\left({\begin{smallmatrix}b_{1}\\[0.7ex]b_{2}\\[0.7ex]b_{3}\end{smallmatrix}}\right)+s\left({\begin{smallmatrix}w_{1}\\[0.7ex]w_{2}\\[0.7ex]w_{3}\end{smallmatrix}}\right)\ \ \,r,s\in \mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2abd54bdd511deb8f299743702e7ee28aa42c83b)





