Kerekítés
|
Read other articles:

Johannes Lebech Menteri Urusan EklesiastikalMasa jabatan21 Desember 2000 – 27 November 2001Perdana MenteriPoul Nyrup Rasmussen PendahuluMargrethe VestagerPenggantiTove Fergo Informasi pribadiLahir12 September 1948 (umur 75)Skive, DenmarkKebangsaanDenmarkPartai politikPartai Liberal Sosial DenmarkAlma materAarhus UniversitetSitus webjohanneslebech.dkSunting kotak info • L • B Niels Johannes Lebech (kelahiran 12 September 1948) adalah seorang politikus Denmark. Ia ...

Anadia, AlagoasMunisipalitasNegara BrasilNegara bagianAlagoasLuas • Total189,473 km2 (73,156 sq mi)Populasi (2010) • Total17.424 • Kepadatan0,092/km2 (0,24/sq mi) Anadia merupakan sebuah munisipalitas yang terletak di negara bagian Brasil di Alagoas. lbs Munisipalitas di AlagoasIbu kota: MaceióArapiraca Arapiraca Campo Grande Coité do Nóia Craíbas Feira Grande Girau do Ponciano Lagoa da Canoa Limoeiro de Anadia São Sebastião T...

Gunung RumatGunung 'AinainTitik tertinggiKetinggian20 m (66 ft)GeografiLetak Madinah, Arab Saudi Gunung Rumat (Arab: جبل الرماة Jabal ar-Rumatcode: ar is deprecated ) atau Gunung 'Ainain adalah sebuah bukit merah yang terletak di sebelah selatan Makam Syuhada Uhud, di samping Wadi Qanat, Madinah, Arab Saudi. Gunung ini disebut Gunung Rumat karena di situ Nabi ﷺ menunjuk 50 orang pemanah (rumat) untuk bersiaga dalam Pertempuran Uhud, yang dikomandani oleh Abdullah bin Jabi...

دوري الدرجة الأولى الروماني 1969–70 تفاصيل الموسم دوري الدرجة الأولى الروماني النسخة 52 البلد رومانيا التاريخ بداية:16 أغسطس 1969 نهاية:22 يوليو 1970 المنظم اتحاد رومانيا لكرة القدم البطل يو تي أي أراد الهابطون بيهور أوراديا مباريات ملعوبة 240 عدد المش...

Terminal SitubondoTerminal Penumpang Tipe BPapan Nama Terminal SitubondoNama lainTerminal MimbaanLokasiJalan Jawa Nomor 1Dusun Mimbaan Barat, Kelurahan Mimbaan, Kecamatan Panji, Kabupaten SitubondoProvinsi Jawa TimurKodepos 68323IndonesiaKoordinat7°42′25″S 114°00′43″E / 7.7068967°S 114.0120125°E / -7.7068967; 114.0120125Koordinat: 7°42′25″S 114°00′43″E / 7.7068967°S 114.0120125°E / -7.7068967; 114.0120125PemilikPemerintah...

Austrian philologist Rudolf MuchBorn(1862-09-07)7 September 1862Vienna, Austrian EmpireDied8 March 1936(1936-03-08) (aged 73)Vienna, AustriaNationalityAustrianAcademic backgroundAlma mater University of Vienna ThesisZur Vorgeschichte Deutschlands (1887)Academic advisorsRichard HeinzelAcademic workDiscipline Classical philology Germanic philology Institutions University of Vienna Notable students Otto Höfler Julius Pokorny Walter Steinhauser Richard Wolfram Siegfried Gutenbrunner Di...

Venceslas Venceslas, roi des Romains (fragment d'un ex-voto de l'archevêque de Prague Jan Očko z Vlašimi). Titre Roi des Romains 10 juin 1376 – 20 août 1400(24 ans, 2 mois et 10 jours) Couronnement 6 juillet 1376 dans la cathédrale d'Aix-la-Chapelle Prédécesseur Charles IV Successeur Robert Ier du Saint-Empire Roi de Bohême 29 novembre 1378 – 16 août 1419(40 ans, 8 mois et 18 jours) Couronnement 15 juin 1363 dans la cathédrale Saint-Guy de Prague P...

Brian Burns Nazionalità Stati Uniti Peso 113 kg Football americano Ruolo Defensive end Squadra New York Giants CarrieraGiovanili 2016-2018 Florida State SeminolesSquadre di club 2019-2023 Carolina Panthers2024- New York Giants Statistiche Partite 64 Partite da titolare 51 Tackle 196 Sack 38,0 Intercetti 0 Fumble forzati 7 Palmarès Trofeo Vittorie Selezioni al Pro Bowl 2 Per maggiori dettagli vedi qui Statistiche aggiornate al 28 marzo 2023 Modifica dati su Wi...

This article is about the AJ Tracey album. For the Lil Mosey song, see Flu Game (song). For the basketball game in the 1997 NBA Finals, see 1997 NBA Finals § Game 5. 2021 studio album by AJ TraceyFlu GameStudio album by AJ TraceyReleased16 April 2021 (2021-04-16)GenreBritish hip hopUK drill[1]afroswing[1]trap[2]R&B[2]Length51:00LabelRevenge RecordsProducerNyge5ive BeatzAJ TraceyAODFred AgainJBJKazzaMark RaggioPxcoyoRemedeeRyfySw...

Cosma Shiva HagenHagen, 2012Lahir17 Mei 1981 (umur 43)Los Angeles, California, A.S.KebangsaanJerman, AmerikaPekerjaanAktrisTahun aktif1996–sekarangOrang tuaNina HagenFerdinand Ferdi KarmelkKerabatEva-Maria Hagen (nenek)Wolf Biermann (kakek-sambung)Otis Chevallier-Hagen (saudara-sambung) Cosma Shiva Hagen (Jerman: [ˈkɔs.ma ˈʃiː.va ˈhaːɡn̩] ⓘ; lahir 17 Mei 1981) adalah aktris dan pengisi suara berdarah Jerman-Amerika. Meskipun dia berbicara bahasa Inggris, peran ...

عنت مسابقة الأغنية الأوروبية تاريخ · القوانين · التصويت · اللغات · البلدان المشاركة · الفائزين · المدن المستضيفة · المقدمين · قائد الفرقةالفنانين المشاركين · إنقطاع · تهاني : 50 سنة من مسابقة يوروفيجن للأغانيسنوات المسابقة 1956 1957 1958 1959 1960 1961 1962 1963 1964 1965 1966 1967 1968 1969 1970 1971 1972 1...

فايتنغ مينيا: فست أف ذا نورث ستار غلاف اللعبة المطور كونامي النظام ألعاب الصالات تاریخ الإصدار فايتنغ مينيا/بونش مينيامارس 2000 العالم بونش مينيا 2ديسمبر 2000 اليابان نظام صندوق الألعاب كونامي نظام 573 و.م.م. R3000A 32 بت مجموعة تعليمات بنية الحاسب processor نظام الصوت بلاي ستيشن إس ب...
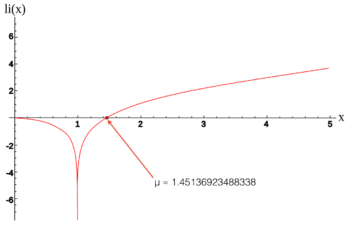
This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Ramanujan–Soldner constant – news · newspapers · books · scholar · JSTOR (April 2024) Ramanujan–Soldner constant as seen on the logarithmic integral function. In mathematics, the Ramanujan–Soldner constant (also called the Soldner constant) is a...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article doit être recyclé (juillet 2021). Une réorganisation et une clarification du contenu paraissent nécessaires. Améliorez-le, discutez des points à améliorer ou précisez les sections à recycler en utilisant {{section à recycler}}. Démolition de la cathédrale du Christ-Sauveur à Moscou sur ordre de Joseph Staline, le 5 décembre 1931. Tout au long de l'histoire de l'Union soviétique (1917 �...

Malaysian politician In this Chinese name, the family name is Ling (林). Yang Amat Berbahagia Tun Dr.Ling Liong SikSSM SPMP DGSM PNBS DPMP DPMS林良实Acting Prime Minister of MalaysiaCovering duties4 February 1988 – 16 February 1988MonarchIskandarPreceded byMahathir MohamadSucceeded byMahathir MohamadChancellor of Universiti Tunku Abdul RahmanIncumbentAssumed office 18 January 2017Preceded byPosition established6th President of the Malaysian Chinese A...

Indian newspaper EbelaAmi amar motoTypeDaily newspaperFormatTabloidOwner(s)ABP GroupEditor-in-chiefArup SarkarEditorAnirban ChattopadhyayLanguageBengaliHeadquarters6, Prafulla Sarkar Street, Kolkata 700001Sister newspapersAnandabazar Patrika, The TelegraphWebsitewww.ebela.in Ebela (Bengali: এবেলা) was a Bengali tabloid targeted primarily at young Bengali readers of West Bengal.[1][2] It is the second Bengali daily published by ABP Group after Anandabazar Patrika. The...

Form of poetry of many languages, originating in Arabic This article is about the poetic form. For other uses, see Ghazal (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ghazal – news · newspapers · books · scholar · JSTOR (October 2011) (Learn how and when to remove this message) An illust...

Sporting event delegationEswatini at theOlympicsIOC codeSWZNOCEswatini Olympic and Commonwealth Games AssociationWebsitewww.socga.org.szMedals Gold 0 Silver 0 Bronze 0 Total 0 Summer appearances19721976–198019841988199219962000200420082012201620202024Winter appearances19921994–2022 Eswatini first participated at the Olympic Games in 1972 (as Swaziland). They missed the next two games but returned for the 1984 Olympics in Los Angeles and have appeared in all the games since then. They made...

劉士篤个人资料字名芳科号號士篤出生1908年?月?日逝世?年?月?日墓地?政党中國國民黨(黨證號特39352〈民27年9月〉、中002135〈民28年7月〉) 劉士篤(1908年—?年),名芳科,號士篤。四川省潼南縣雙江鎮人,法學家。曾任律師,監察院監察委員、立法院立法委員。[1] 生平 1930年,畢業于國立中央大學法律系 法官訓練所第三屆畢業,中央訓練團黨政班第二期畢...

Quello che segue è un elenco dei sovrani che hanno regnato sul marchesato del Monferrato, prima, e sul ducato del Monferrato, poi. L'elenco include tutti i sovrani, prima Marchesi e poi Duchi, appartenenti alle quattro dinastie che si sono susseguite nel dominio del Monferrato, ovvero: gli Aleramici, i Paleologi, i Gonzaga, e i Gonzaga-Nevers. Indice 1 Marchesi del Monferrato 1.1 Aleramici (967 – 1305) 1.2 Paleologi (1306 – 1533) 1.3 Gonzaga (1533 – 1574) 2 Duchi del Monferrato 2.1 Gon...
















































