IEEE lebegőpontos számformátum
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Yayasan Universitas LabuhanbatuSekolah Tinggi Ilmu Ekonomi LabuhanbatuLogo Sekolah Tinggi Ilmu Ekonomi LabuhanbatuMotoMemimpin Peradaban BangsaMoto dalam bahasa InggrisLed The Nation CivilizationJenisPerguruan tinggi di Sumatera UtaraDidirikan29 ...
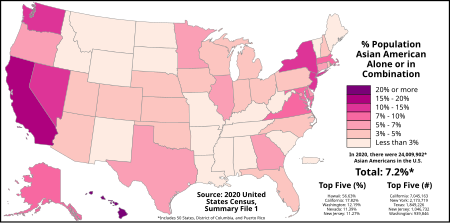
Americans of Asian ancestry This article is about the U.S. population of Americans of Asian ancestry. For populations of Asians across the Americas, see Asians in the Americas. For the documentary series, see Asian Americans (film series). Asian AmericansDistribution of Asian Americans by countyTotal population 24,009,902 (alone and in combination)7.2% of the population (2020)[1] Chinese Americans: 5,143,982Indian Americans: 4,506,308Filipino Americans: 4,089,570Vietnamese Americans: ...

Matteo Maria ZuppiUskup Agung BolognaGerejaGereja Katolik RomaKeuskupan agungBolognaTakhtaBolognaPenunjukan27 Oktober 2015Awal masa jabatan12 Desember 2015PendahuluCarlo CaffarraJabatan lainKardinal-Imam Sant'Egidio (2019-)ImamatTahbisan imam9 Mei 1981oleh Renato SpallanzaniTahbisan uskup14 April 2012oleh Agostino ValliniPelantikan kardinal5 Oktober 2019oleh Paus FransiskusPeringkatKardinal-ImamInformasi pribadiLahir11 Oktober 1955 (umur 68)Roma, ItaliaKewarganegaraan Ital...

My Little Pony - L'amicizia è magicaserie TV d'animazione Logo italiano della serie. Titolo orig.My Little Pony: Friendship Is Magic Lingua orig.inglese PaeseStati Uniti, Canada AutoreLauren Faust RegiaJayson Thiessen, James Wootton SceneggiaturaLauren Faust, Amy Keating Rogers, Cindy Morrow, Chris Savino, Meghan McCarthy, Charlotte Fullerton, M. A. Larson, Dave Polsky, Merriwether Williams MusicheWilliam Kevin Anderson, Daniel Ingra...

Battle of the Greek War of Independence Battle of SculeniPart of the Wallachian Uprising of the Greek War of IndependenceAthanasios Agrafiotis fights in Pruthby Peter von HessDate29 June 1821LocationSculeni, Principality of Moldavia, Ottoman Empire47°19′N 27°38′E / 47.317°N 27.633°E / 47.317; 27.633Result Ottoman victoryBelligerents Greek revolutionaries Ottoman EmpireCommanders and leaders George KantakouzenosGiorgakis OlympiosYiannis PharmakisAthanasios Agraf...

American election 2017 Minneapolis mayoral election ← 2013 November 7, 2017 (2017-11-07) 2021 → Candidate Jacob Frey Raymond Dehn Betsy Hodges Party Democratic (DFL) Democratic (DFL) Democratic (DFL) First round 26,116(25.0%) 18,101(17.3%) 18,915(18.1%) Final round 46,716(57.2%) 34,791(42.8%) Eliminated Candidate Tom Hoch Nekima Levy-Pounds Party Democratic (DFL) Democratic (DFL) First round 20,125(19.3%) 15,716(15.0%) Final round Eliminated ...
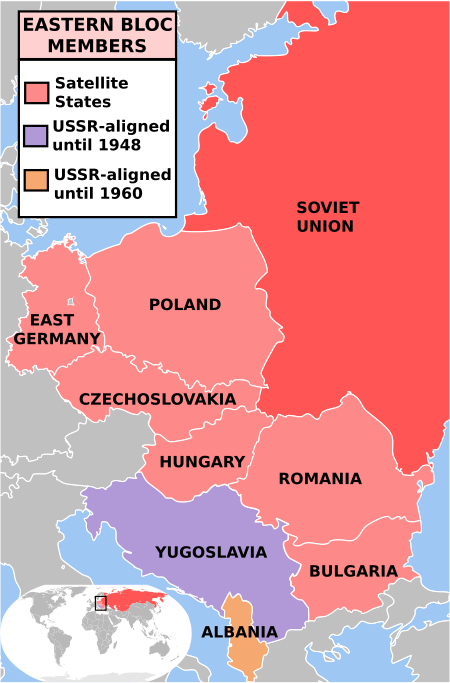
Cold War-era Soviet foreign policy aimed at justifying foreign military interventions Eastern Bloc: the USSR and its satellite states The Brezhnev Doctrine was a Soviet foreign policy that proclaimed that any threat to socialist rule in any state of the Soviet Bloc in Central and Eastern Europe was a threat to all of them, and therefore, it justified the intervention of fellow socialist states. It was proclaimed in order to justify the Soviet-led occupation of Czechoslovakia earlier in 1968, ...

Dalam artikel ini, nama keluarganya adalah Mallarangeng, nama keluarga patronimik Bugis; Andi adalah gelar kehormatan bangsawan Bugis. Andi Mallarangeng Menteri Pemuda dan Olahraga Indonesia ke-10Masa jabatan20 Oktober 2009 – 7 Desember 2012PresidenSusilo Bambang YudhoyonoWakil PresidenBoedionoPendahuluAdhyaksa DaultPenggantiAgung Laksono(Pelaksana Tugas)Roy SuryoJuru Bicara Presiden Republik Indonesia ke-6Masa jabatan21 Oktober 2004 – 20 Oktober 2009Menjabat ...

Disney media franchise based on the Alice books by Lewis Carroll See also: Portrayals of Alice in Wonderland § Disney Alice in WonderlandAbove: A logo used to represent the 1951 animated filmBelow: Logo used for the 2010 live-action filmCreated byWalt DisneyOriginal workAlice in Wonderland (1951)OwnerThe Walt Disney CompanyBased onAlice's Adventures in Wonderland and Through the Looking-Glassby Lewis CarrollFilms and televisionFilm(s) Alice in Wonderland (1951; animated) Alice in Wonder...

Pour les articles homonymes, voir Ixion (homonymie). IxionFonctionRoi des Lapithes (d)BiographiePère Éton (d) ou Antion (en) ou Arès ou Phlégias ou LéontéeConjoint DiaEnfants Abas (d)CentaurosPirithoosTisadia (d)modifier - modifier le code - modifier Wikidata José de Ribera, Ixion, 1632, musée du Prado. Dans la mythologie grecque, Ixion (en grec ancien Ἰξίων / Ixiôn), fils d'Antion et de Périmèle (ou de Léontos selon Hygin, ou de Phlégias selon des scholies), est un Lapith...

Federal electoral district in Quebec, Canada This article is about the federal district. For the provincial district, see Mont-Royal (provincial electoral district). Mount Royal Quebec electoral districtMount Royal in relation to other federal electoral districts in Montreal and LavalFederal electoral districtLegislatureHouse of CommonsMP Anthony HousefatherLiberalDistrict created1924First contested1925Last contested2021District webpageprofile, mapDemographicsPopulation (201...

International maritime treaty Agreement Concerning the Shipwrecked Vessel RMS TitanicDrafted6 November 2003LocationLondon, United KingdomEffective18 November 2019 (18 November 2019)ConditionConsent to be bound by two partiesParties United Kingdom United StatesDepositaryGovernment of the United Kingdom of Great Britain and Northern IrelandLanguageEnglish and FrenchFull text Agreement Concerning the Shipwrecked Vessel RMS Titanic at Wikisource The Agreement Concerning the Shipwre...

LiaoningLa Liaoning ad Hong Kong nel 2017Descrizione generale Tipoportaerei ClasseAdmiral Kuznecov In servizio con Marina dell'EPL Identificazione16 CantiereCantieri navali di Nikolaev Impostazione6 dicembre 1985 Varo4 dicembre 1988 CompletamentoDalian, 27 luglio 2011 Consegna11 settembre 2012 Entrata in servizio25 novembre 2016 Nomi precedentiRiga, Varjag Caratteristiche generaliDislocamento60.000/66.000 t Lunghezza304,5 m Larghezza75 m Pescaggio10,5 m Propulsione8 caldaie...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Byfleet – news · newspapers · books · scholar · JSTOR (January 2023) (Learn how and when to remove this message) Village in EnglandByfleetVillageByfleet Village HallByfleetLocation within SurreyArea6.24 km2 (2.41 sq mi)Population7,724 (ward,...

La Madama redirects here. For the border settlement on the northeast frontier of Niger, see Madama. For the Italian association football club often known by this nickname, see Juventus F.C. 1976 filmSexycopDirected byDuccio TessariScreenplay by Massimo Felisatti Fabio Pittorru Duccio Tessari[1] Based onLa Madamaby Massimo FelisattiFabio PittorruProduced byGiorgio Venturini[1]Starring Christian De Sica Ines Pellegrini Oreste Lionello CinematographyGiulio Albonico[1]Edit...

German footballer (born 1988) You can help expand this article with text translated from the corresponding article in German. (March 2022) Click [show] for important translation instructions. View a machine-translated version of the German article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated ...

Scottish footballer For the rugby union footballer, see Euan Murray. Euan Murray Murray warming up for Hartlepool United in 2022Personal informationFull name Euan MurrayDate of birth (1994-01-20) 20 January 1994 (age 30)[1]Place of birth Rutherglen, Scotland[1]Height 6 ft 1 in (1.85 m)[1]Position(s) Defender / Defensive MidfielderTeam informationCurrent team Raith RoversNumber 6Youth career MotherwellSenior career*Years Team Apps (Gls)2011–2014 Mo...

GeometriProyeksi sebuah lingkaran pada sebuah bidang Garis besarSejarah Cabang Euklides takEuklides Elips Bola Hiperbola Geometri non-Archimedes Projektif Afin Sintetis Analitis Aljabar Aritmetika Diophantus Diferensial Riemann Simplektik Diferensial diskret Kompleks Tentu Diskrit Digital Cembung Komputasi Fraktal Insidens KonsepTampilanDimensi Melukis dengan penggaris dan jangka busur Sudut Kurva Diagonal Ortogonalitas (tegak lurus) Sejajar Titik pojok Kekongruenan Keserupaan Simetri Dimensi...

US Open 1987Sport Tennis Data1º settembre - 14 settembre Edizione107ª CategoriaGrande Slam (ITF) SuperficieCemento LocalitàNew York negli Stati Uniti ImpiantoUSTA Billie Jean King National Tennis Center, Flushing Meadows CampioniSingolare maschile Ivan Lendl Singolare femminile Martina Navrátilová Doppio maschile Stefan Edberg / Anders Järryd Doppio femminile Martina Navrátilová / Pam Shriver Doppio misto Martina Navrátilová / Emilio Sánchez 1986 1988 Lo US Open 1987 è stata la 10...

Pakistani election 2018 Khyber Pakhtunkhwa provincial election ← 2013 25 July 2018 2019 (FATA seats) →2024 → elected members →All 124 seats in the Khyber Pakhtunkhwa Assembly63 seats needed for a majorityOpinion pollsTurnout45.52%(0.78%pp)[1] First party Second party Third party Leader Pervez Khattak Akram Khan Durrani Haider Khan Hoti Party PTI MMA ANP Leader's seat Nowshera-INowshera-IV Bannu-IV Mardan-VI Last election ...



