Floyd–Warshall-algoritmus
Kategória	Legrövidebb út probléma (súlyozott gráfok esetében)
Adatstruktúra	Gráf
Legrosszabb időbonyolultság	${\displaystyle \Theta (|V|^{3})}$
Legjobb időbonyolultság	${\displaystyle \Theta (|V|^{3})}$
Átlagos idő bonyolultság	${\displaystyle \Theta (|V|^{3})}$
Legrosszabb tár bonyolultság	${\displaystyle \Theta (|V|^{2})}$

A számítástechnikában a Floyd–Warshall-algoritmus (más néven Floyd–algoritmus, a Roy–Warshall-algoritmus, a Roy–Floyd-algoritmus vagy az ún. WFI-algoritmus ) egy olyan algoritmus, amely a megtalálja legrövidebb útvonalakat egy pozitív vagy negatív élsúlyú súlyozott gráfban . (de negatív körök nélkül).^[1][2] Az algoritmus egyetlen végrehajtása megtalálja az összes csúcspár közötti legrövidebb távolságok hosszát (összesített súlyát). Annak ellenére, hogy nem adja vissza az útvonalak részleteit, lehetséges az útvonalak rekonstruálása az algoritmus egyszerű módosításával. Az algoritmus egyes változatai arra is használhatóak, hogy megtaláljunk egy a valós számokkal összefüggésben levő tranzitív lezárást, vagy (a Schulze-módszerrel összefüggésben) a legszélesebb útvonalakat az összes csúcspár között egy súlyozott grafikonon.

A Floyd–Warshall-algoritmus a dinamikus programozás egy jól ismert példája, melyet Robert Floyd publikált 1962-ben.^[3] Alapvetően megegyezik azon algoritmusokkal, melyeket korábban Bernard Roy 1959-ben kiadott^[4] és továbbá Stephen Warshall 1962-ben ^[5] egy grafikon tranzitív lezárásának a megállapítására, és szorosan kapcsolódik Kleene algoritmusához (1956-ban lett közzétéve) amely témája egy determinisztikus véges automata konvertálása szabályos kifejezésekké.^[6] Az algoritmus modern formuláját azaz a három egymásba ágyazott hurkot (for ciklust) először Peter Ingerman fogalmazta meg, szintén 1962-ben.^[7]

A Floyd–Warshall algoritmus összehasonlítja az összes lehetséges utat a grafikonon az egyes csúcspárok között. Képes ezt megtenni ${\displaystyle \Theta (|V|^{3})}$ összehasonlítással egy gráfban, bár lehet, hogy akár ${\displaystyle \Omega (|V|^{2})}$ él van a grafikonon, és az élek minden kombinációját szükséges tesztelni. Ez úgy történik, hogy fokozatosan javítja a becslést a két csúcs közötti legrövidebb útvonalra vonatkozóan, amíg a becslés nem lesz optimális.

Vegyünk egy ${\displaystyle G}$ grafikont,${\displaystyle V}$ csúcsokkal 1-től ${\displaystyle N}$-ig számozva. Továbbá egy függvényt az ún. ${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,k)}$ amely visszatér a legrövidebb útvonallal ${\displaystyle i}$ és ${\displaystyle j}$ között adott csúcsok használatával: ${\displaystyle \{1,2,\ldots ,k\}}$ közbenső pontként a csúcsok mentén. Figyelembe véve az adott függvényt a célunk az, hogy megtaláljuk a legrövidebb utat minden ${\displaystyle i}$ -től minden ${\displaystyle j}$-ig bármelyik csúcs használatával: ${\displaystyle \{1,2,\ldots ,N\}}$.

A csúcspárok mindegyikénél a ${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,k)}$ lehet akár

(1) egy útvonal, amely nem megy át ${\displaystyle k}$-n (amely csak az adott csúcsokat használja: ${\displaystyle \{1,\ldots ,k-1\}}$)

vagy

(2) egy útvonal, amely végigmegy ${\displaystyle k}$-n (${\displaystyle i}$-től ${\displaystyle k}$-ig és aztán ${\displaystyle k}$-tól ${\displaystyle j}$-ig, mindkét esetben az adott közbenső csúcsokat használva:  ${\displaystyle \{1,\ldots ,k-1\}}$

Tudjuk, hogy a legjobb útvonal ${\displaystyle i}$-től ${\displaystyle j}$-ig az amely csak azon csúcsokat használja amik ${\displaystyle 1}$-en keresztül ${\displaystyle k-1}$ vannak meghatározva a ${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,k-1)}$ által, és egyértelmű, hogy ha jobb útvonal lenne ${\displaystyle i}$-től ${\displaystyle k}$-ig majd onnan ${\displaystyle j}$-ig, akkor ezen útvonalnak a hossza lenne a legrövidebb út láncolata az ${\displaystyle i}$-től a ${\displaystyle k}$-ig (csak a közbenső csúcsok használatával ${\displaystyle \{1,\ldots ,k-1\}}$) és a legrövidebb a ${\displaystyle k}$-tól ${\displaystyle j}$-ig (csak a közbenső csúcsok használatával  ${\displaystyle \{1,\ldots ,k-1\}}$).

Ha ${\displaystyle w(i,j)}$ az él súlya az adott ${\displaystyle i}$ és ${\displaystyle j}$ csúcsok között, akkor meghatározhatjuk a ${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,k)}$ függvényt a következő rekurzív képlet szerint:

${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,0)=w(i,j)}$

a rekurzív eset a következő:

${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,k)=}$

${\displaystyle \mathrm {min} {\Big (}\mathrm {legrovidebbUtvonal} (i,j,k-1),}$

${\displaystyle \mathrm {legrovidebbUtvonal} (i,k,k-1)+\mathrm {legrovidebbUtvonal} (k,j,k-1){\Big )}}$.

Ez a képlet a Floyd–Warshall algoritmus szive. Az algoritmus futása során először kiszámolja a ${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,k)}$ alapján az ${\displaystyle (i,j)}$ pároknak a ${\displaystyle k=1}$, majd ${\displaystyle k=2}$ és így tovább. Ez a folyamat addig folytatódik, amíg ${\displaystyle k=N}$, és megtaláltuk a legrövidebb utat mindegyik ${\displaystyle (i,j)}$ páros számára bármilyen közbenső csúcs használatával. Az alapváltozat pszeudókódja a következő:

Legyen az ún. 'tavolsag' a |V| × |V| minimális távolságok tömbje, amely inicializálva ∞-ig (végtelen)
for each el (u, v) do
    tavolsag[u][v] ← w(u, v)  // Az adott él súlya (u, v)
for each csucs v do
    tavolsag[v][v] ← 0
for k from 1 to |V|
    for i from 1 to |V|
        for j from 1 to |V|
            if tavolsag[i][j] > tavolsag[i][k] + tavolsag[k][j] 
                tavolsag[i][j] ← tavolsag[i][k] + tavolsag[k][j]
            end if

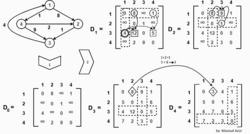
A fenti algoritmust az alább látható bal oldali grafikonon láthatjuk:

A külső hurok első rekurziója előtt, a fenti k = 0 jelöléssel láthatjuk, az egyetlen ismert útvonalat amely megfelel a grafikon egyes széleinek. k = 1 esetén mindössze 1 útvonal található amely áthalad a csúcson: a [2,1,3] útvonal, amely helyettesíti a [2,3] útvonalat, amelynek kevesebb éle van, de hosszabb (súly szempontjából). A k = 2 esetén az {1,2} csúcsokon átmenő utak találhatók. A piros és a kék négyzet megmutatja, hogy a [4,2,1,3] út, hogy állt össze a korábbi iterációkban felismert két útvonalból a [4,2] és [2,1,3]-ból 2-vel a metszéspontban. A [4,2,3] elérési utat nem vesszük figyelembe, mivel a [2,1,3] a legrövidebb út, amelyet eddig a 2-től 3-ig megfigyeltünk. A k = 3 esetén a {1,2,3} csúcsokon átmenő utak találhatók. Végül, k = 4 -nél az összes legrövidebb útvonal megtalálható.

A távolság mátrixa minden k iterációnál, a frissített távolságokkal (vastag betűvel jelölve):

A gráfelméletben értelmezett negatív kör egy olyan kör, ahol az élek összege negatív értékhez vezet. Legrövidebb út nem fellelhető egyetlen ${\displaystyle i}$, ${\displaystyle j}$ csúcspár között sem, amelyek egy negatív kör részét képezik, mert az út hossza ${\displaystyle i}$-től ${\displaystyle j}$-ig tetszőlegesen kicsi (negatív). Numerikusan értelmezhető kimeneti értékhez a Floyd – Warshall algoritmus feltételezi, hogy nincs negatív kör. Mindazonáltal, ha vannak negatív körök, a Floyd – Warshall algoritmus felhasználható arra, hogy felismerje ezeket. Az intuíció a következő:

• A Floyd–Warshall algoritmus iteratív módon felülvizsgálja az út hosszát az összes csúcspár között ${\displaystyle (i,j)}$, beleértve azon eseteket ahol ${\displaystyle i=j}$ ;
• Az út hossza ${\displaystyle (i,i)}$ kezdetben nulla;
• Egy adott út ${\displaystyle [i,k,\ldots ,i]}$ csak javulhat, ha a hossza kisebb mint nulla, vagyis negatív kört jelöl;
• Az algoritmus után ${\displaystyle (i,i)}$ negatív lesz, ha létezik negatív hosszúságú útvonal az ${\displaystyle i}$ és ${\displaystyle i}$ között.

Ennélfogva a negatív körök, Floyd – Warshall algoritmussal történő felismeréséhez meg kell vizsgálni az út mátrix átlóját, a vizsgálat során negatív szám jelenléte jelzi, hogy a grafikon legalább egy negatív kört tartalmaz.^[8] A numerikus problémák elkerülése érdekében ellenőrizni kell, hogy vannak-e negatív számok az útvonal mátrixának átlójában az algoritmus belső ciklusán belül.^[9] Nyilvánvalóan egy irányítatlan gráfban a negatív él negatív kört (azaz zárt bejárást) hoz létre az érintett csúcsokkal. Figyelembe véve a fenti példa gráfjának minden éle irányítatlan, pl. a 4 - 2 - 4 csúcsszekvencia egy kör, amelynek súlya −2.

A Floyd–Warshall algoritmus általában a csúcspárok közötti útvonalakat adja meg. Azonban egyszerű módosításokkal lehetséges olyan eljárást készíteni ami helyreállítja az útvonalat bármely két végpont csúcsa között. Van rá lehetőség, hogy eltároljuk a tényleges útvonalat az egyik csúcstól egy adott másik csúcshoz, de ez nem szükséges, sőt tárhelyfelhasználás (memória) szempontjából eléggé költséges. Ehelyett a legrövidebb útvonal kiszámítható minden egyes ${\displaystyle \Theta (|E|)}$ csomópontoknak, ${\displaystyle \Theta (|V|)}$ idő alatti tárhely felhasználásával amely az egyes fák tárolására szolgáló memória, amely lehetővé teszi számunkra, hogy hatékonyan rekonstruáljunk egy utat bármely két csatlakoztatott csúcsból.

Legyen az ún. 'tavolsag' ${\displaystyle |V|\times |V|}$ minimális távolságok tömbje, inicializálva ${\displaystyle \infty }$-ig(végtelen)
Legyen a 'kovetkezo' a ${\displaystyle |V|\times |V|}$ csúcsindexek tömbje amely null értékkel inicializálódik.

procedure FloydWarshallUtvonalHelyreallitassal() is
    for each el (u, v) do
        tavolsag[u][v] ← w(u, v)  // Az adott él súlya (u, v)
        kovetkezo[u][v] ← v
    for each csucs v do
        tavolsag[v][v] ← 0
        kovetkezo[v][v] ← v
    for k from 1 to |V| do // általános Floyd-Warshall implementáció
        for i from 1 to |V|
            for j from 1 to |V|
                if tavolsag[i][j] > tavolsag[i][k] + tavolsag[k][j] then
                    tavolsag[i][j] ← tavolsag[i][k] + tavolsagg[k][j]
                    kovetkezo[i][j] ← kovetkezo[i][k]

procedure Utvonal(u, v)
    if tavolsag[u][v] = null then
        return []
    ut = [u]
    while u ≠ v
        u ← kovetkezo[u][v]
        ut.append(u)
    return ut

Legyen ${\displaystyle n}$ a ${\displaystyle |V|}$, azaz a csúcsok száma . Ahhoz, hogy megtaláljuk az összes ${\displaystyle n^{2}}$ értéket a ${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,k)}$-hoz tartozóan (minden ${\displaystyle i}$ és ${\displaystyle j}$) azokból ahol a ${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,k-1)}$, ${\displaystyle 2n^{2}}$ számú műveletet igényel. Mivel úgy kezdünk, hogy a ${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,0)=elKoltseg(i,j)}$ és kiszámítjuk az adott ${\displaystyle n}$ mátrixok ${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,1)}$, ${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,2)}$, ${\displaystyle \ldots }$, ${\displaystyle \mathrm {legrovidebbUtvonal} (i,j,N)}$, összes használt műveletnek a számát, ami: ${\displaystyle n\cdot 2n^{2}=2n^{3}}$. Ezért az algoritmus bonyolultsága: ${\displaystyle \Theta (n^{3})}$.

A Floyd – Warshall algoritmus felhasználható többek között a következő problémák megoldására:

• A legrövidebb útvonal számítására irányított gráfokban (Floyd algoritmusa).
• Irányított gráfok tranzitív lezárására (Warshall algoritmus). Eredeti megfogalmazásában a Warshall algoritmusban a gráf nem súlyozott, és egy logikai szomszédsági mátrix képviseli. Az összeadási műveletet helyettesíti a logikai összekapcsolás (ÉS), a minimális művelet pedig logikus diszjunció (VAGY).
• Véges automata által elfogadott szabályos nyelvet jelölő reguláris kifejezés keresése ( Kleene algoritmusa, amely egy szorosan kapcsolódó általánosítása a Floyd – Warshall algoritmusnak) ^[11]
• Valós mátrixok inverziója ( Gauss – Jordan algoritmus ) ^[12]
• Optimális útvonal választás. Ebben az alkalmazásban az érdekesség megtalálni az utat a két csúcs között, maximális áramlással. Ahelyett, hogy a minimumokat vennénk mint a fentebb látható pszeudókódban is, inkább a maximumokat vesszük. Az élek súlya rögzített kényszert reprezentál az áramlásban. Az útvonal súlya ún. szűkületet ábrázol; így a fenti összeadás műveletet a minimális művelet váltja fel.
• A Pathfinder (útvonal-kereső) hálózatok gyors kiszámítása.
• Legszélesebb útvonalak / Maximális sávszélesség-útvonalak
• A különbséghez kötött mátrixok (DBM) kanonikus formájának kiszámítása
• A gráfok közötti hasonlóság kiszámítása

Az algoritmus megvalósításai megannyi programozási nyelven rendelkezésre állnak.

• C++ esetén boost::graph könyvtár
• C# esetén a QuickGraph
• Továbbá C# esetén a QuickGraphPCL (Hasonló a QuickGraph-hoz azonban jobb kompatibilitással rendelkezik azon projekteknél amik PCL-t használnak.)
• Java esetén az Apache Commons Graph könyvtár
• JavaScript esetén a Cytoscape könyvtár
• MATLAB esetén a Matlab_bgl csomag
• Perl esetén Graph modul
• Python esetén a SciPy könyvtárban (a scipy.sparse.csgraph modul) vagy NetworkX könyvtár
• R esetén a e1071 és Rfast

A Floyd – Warshall algoritmus jó választás az útvonal kiszámításához az összes csúcspár között sűrű grafikonokban, amelyekben a csúcsok többségét vagy az összeset élek kötik össze. A nem negatív élsúlyú ritka gráfok esetében jobb választás, ha Dijkstra algoritmusát használjuk minden lehetséges kezdőpontból, mivel az ismételt Dijkstra futási ideje ( ${\displaystyle O(|E||V|+|V|^{2}\log |V|)}$ (Fibonacci halom) jobb, mint ${\displaystyle O(|V|^{3})}$ a Floyd – Warshall algoritmus futási ideje, amikor ${\displaystyle |E|}$ jelentősen kisebb, mint ${\displaystyle |V|^{2}}$. A negatív élekkel rendelkező, de negatív körök nélküli ritka gráfoknál Johnson algoritmusa használható, ugyanolyan futási idővel, mint az ismételt Dijkstra megközelítésnél.

Vannak ismert algoritmusok, amelyek gyors mátrixszorzást használnak az összes pár legrövidebb útjának kiszámításához sűrű grafikonokban, ám ezek általában további kikötéseket fogalmaznak meg az élsúlyokhoz (például előírják, hogy kis egész számok legyenek).^[13][14] Ezen túlmenően a futási idejükben fellelhető állandó tényezők miatt csak a nagyon nagy grafikonok esetében lennének gyorsabbak mint a Floyd – Warshall algoritmus.

• A Floyd – Warshall algoritmus interaktív animációja
• A Floyd – Warshall algoritmus interaktív animációja (Müncheni Műszaki Egyetem) Archiválva 2019. október 30-i dátummal a Wayback Machine-ben

Ez a szócikk részben vagy egészben a Floyd–Warshall algorithm című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.