Az aritmetika alapjai (Frege)
|
Read other articles:

Kekayi Kekayi atau Kaikeyi (Sanskerta: कैकेयी; Kaikeyī) adalah permaisuri Raja Dasarata dalam wiracarita Ramayana. Ia merupakan wanita ketiga yang dinikahi Dasarata setelah dua permaisurinya yang lain tidak mampu memiliki putera. Pada saat Dasarata meminang dirinya, ayah Kekayi membuat perjanjian dengan Dasarata bahwa putera yang dilahirkan oleh Kekayi harus menjadi raja. Dasarata menyetujui perjanjian tersebut karena dua permaisurinya yang lain tidak mampu melahirkan putera. Nam...

Peta lokasi Kabupaten Hulu Sungai Tengah Berikut ini adalah daftar kecamatan dan kelurahan/desa di Kabupaten Hulu Sungai Tengah, Provinsi Kalimantan Selatan, Indonesia. Kabupaten Hulu Sungai Tengah terdiri dari 11 kecamatan, 8 kelurahan, dan 161 desa. Pada tahun 2017, jumlah penduduknya mencapai 250.782 jiwa dengan luas wilayah 1.472,00 km² dan sebaran penduduk 170 jiwa/km².[1][2] Daftar kecamatan dan kelurahan di Kabupaten Hulu Sungai Tengah, adalah sebagai berikut: Kode Ke...

Untuk kegunaan lain, lihat Kala (disambiguasi). KalaSutradaraJoko AnwarProduserDhamoo Punjabi Manoj PunjabiDitulis olehJoko AnwarPemeranFachri Albar Ario Bayu ShantyPenata musikZeke KhaseliAghi NarottamaSinematograferIpung Rachmat SyaifulPenyuntingWawan I. WibowoPerusahaanproduksiMD PicturesDistributor Disney+ Hotstar WeTV iflix CatchPlay Tanggal rilis 19 April 2007 (2007-04-19) (Indonesia) Durasi102 menitNegaraIndonesiaBahasaBahasa Indonesia Penghargaan Festival Film Indonesia...

الثقافة الأعلام والتراجم الجغرافيا التاريخ الرياضيات العلوم المجتمع التقانات الفلسفة الأديان فهرس البوابات علوم: تاريخ العلوم فلسفة العلوم رياضيات ف...

لمعانٍ أخرى، طالع بيتر ستون (توضيح). بيتر ستون معلومات شخصية الميلاد 27 فبراير 1930 لوس أنجلوس الوفاة 26 أبريل 2003 (73 سنة) نيويورك سبب الوفاة تليف رئوي مواطنة الولايات المتحدة الأب جون ستون الحياة العملية الاسم الأدبي Pierre Marton، وPeter Joshua المدرسة...

У этого термина существуют и другие значения, см. Зыбка. Китай Стокгольм Река Амур Зыбка (подъёмка) — рыболовная сеть, натянутая на четырёхугольную раму (или растянутая между двумя перекрещенными металлическими или деревянными стержнями), привешиваемая к тонкому конц...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (أغسطس 2023) يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة ...

Cet article concerne la ville allemande de Dachau. Pour le camp de concentration nazi, voir Camp de concentration de Dachau. Dachau Armoiries Administration Pays Allemagne Land Bavière District(Regierungsbezirk) Haute-Bavière Arrondissement(Landkreis) Dachau Bourgmestre(Bürgermeister) Florian Hartmann Code postal 85221 Code communal(Gemeindeschlüssel) 09 1 74 115 Indicatif téléphonique 08131 Immatriculation DAH Démographie Gentilé dachavien/ne Population 44 822 hab. (31...

BridgeKanuni Sultan Suleiman bridgeCoordinates41°01′19″N 28°34′14″E / 41.021944°N 28.570556°E / 41.021944; 28.570556CrossesLake BüyükçekmeceOfficial nameKanuni Sultan Süleyman KöprüsüCharacteristicsTotal length636 m (2,087 ft)Width7.17 m (23.5 ft)No. of spans28HistoryConstruction start1566Opened1567; 457 years ago (1567)Location The Kanuni Sultan Suleiman bridge (Turkish: Kanuni Sultan Süleyman Köprüsü), also...
周處除三害The Pig, The Snake and The Pigeon正式版海報基本资料导演黃精甫监制李烈黃江豐動作指導洪昰顥编剧黃精甫主演阮經天袁富華陳以文王淨李李仁謝瓊煖配乐盧律銘林孝親林思妤保卜摄影王金城剪辑黃精甫林雍益制片商一種態度電影股份有限公司片长134分鐘产地 臺灣语言國語粵語台語上映及发行上映日期 2023年10月6日 (2023-10-06)(台灣) 2023年11月2日 (2023-11-02)(香�...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Questa voce sull'argomento contee del Michigan è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di LivingstonconteaLocalizzazioneStato Stati Uniti Stato federato Michigan AmministrazioneCapoluogoHowell Data di istituzione1836 TerritorioCoordinatedel capoluogo42°36′00″N 83°54′36″W / 42.6°N 83.91°W42.6; -83.91 (Contea di Livingston)Coordinate: 42°36′00″N 83°54′36″W / 42.6°N 83.91°...

Ahab, raja Israel Ahab adalah raja ke-7 Kerajaan Israel (Samaria) menurut Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Ia menggantikan ayahnya, Omri, dan ia menikah dengan Izebel, puteri Etbaal, raja orang Sidon. Ahab sangat dipengaruhi dan dikuasai oleh Izebel.[1] Ahab sangat patuh mendengarkan perkataan Nabi Elia untuk berbakti kepada Tuhan, tetapi ia sangat lemah dalam melawan Izebel. Israel semakin jatuh di bawah pemerintahannya karena penyembahan berhala yang dilakukan ...

هذه المقالة عن الأعصاب في الكائنات الحية. لمعانٍ أخرى، طالع عصب (توضيح). عصبمعلومات عامةصنف فرعي من نسيج عصبيsegment of neural tree organ (en) [1]كيان تشريحي معين جزء من جهاز عصبي محيطي لديه جزء أو أجزاء محور عصبي تعديل - تعديل مصدري - تعديل ويكي بيانات العصب[2] هو حزمة داخلية م...

American baseball player (born 1984) Baseball player Cesar CarrilloCarrillo pitching for the San Diego Padres in 2009Starting pitcherBorn: (1984-04-29) April 29, 1984 (age 40)Chicago, IllinoisBats: RightThrows: RightProfessional debutMLB: August 13, 2009, for the San Diego PadresCPBL: March 21, 2012, for the Brother ElephantsMLB statistics (through 2009)Win–loss record14-22Earned run average4.44Strikeouts78 Teams San Diego Padres (2009) Brother Elephants (...

شرق آسيا الإحداثيات 47°12′37″N 102°50′52″E / 47.210277777778°N 102.84777777778°E / 47.210277777778; 102.84777777778 تقسيم إداري البلد اليابان كوريا الجنوبية كوريا الشمالية الصين منغوليا تايوان روسيا فيتنام[1] خصائص جغرافية المساحة 11839074 كيلومتر مربع رمز جيونيمز 7729894&...

British actress and model (1980–2009) Lucy GordonGordon at the 2007 premiere of Spider-Man 3Born(1980-05-22)22 May 1980Oxford, Oxfordshire, EnglandDied20 May 2009(2009-05-20) (aged 28)Paris, FranceOccupations Actress model Years active1995–2009 Lucy Gordon (22 May 1980 – 20 May 2009) was an English actress and model. She became a face of CoverGirl in 1997 before starting an acting career. Her first film was Perfume in 2001 before going on to have small roles in Spider-Man 3, S...

Range of frequencies or wavelengths of electromagnetic radiation A diagram of the electromagnetic spectrum, showing various properties across the range of frequencies and wavelengths The electromagnetic spectrum is the full range of electromagnetic radiation, organized by frequency or wavelength. The spectrum is divided into separate bands, with different names for the electromagnetic waves within each band. From low to high frequency these are: radio waves, microwaves, infrared, visible ligh...

Departementet Corrèzes läge i Frankrike. Detta är en lista över de 286 kommunerna i departementet Corrèze i Frankrike. Insee-nummer Postnummer Kommun 19001 19260 Affieux 19002 19200 Aix 19003 19190 Albignac 19004 19380 Albussac 19005 19240 Allassac 19006 19200 Alleyrat 19007 19120 Altillac 19008 19250 Ambrugeat 19009 19000 Les Angles-sur-Corrèze 19010 19400 Argentat 19011 19230 Arnac-Pompadour 19012 19120 Astaillac 19013 19190 Aubazine 19014 19220 Auriac 19015 19310 Ayen 19016 19800 Bar...
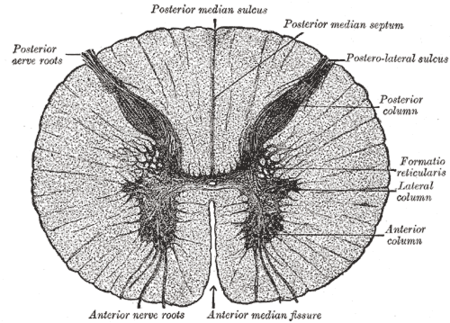
Anterior median fissure of spinal cordA spinal nerve with its anterior and posterior roots.Transverse section of the spinal cord in the mid-thoracic region.DetailsIdentifiersLatinfissura mediana anterior medullae spinalisTA98A14.1.02.007TA26053FMA83735Anatomical terminology[edit on Wikidata] The anterior median fissure of the spinal cord is a deep midline groove of the anterior/ventral spinal cord.[1]: 486 It divides the white matter of the anterior spinal cord ne...