Alacsony dimenziÃģs topolÃģgia
|
Read other articles:

Kuil Brihadeshwara dilihat dari sebelah kanan depan, dengan gaya Dravida Tempat suci Hindu adalah suatu tempat maupun bangunan yang dikeramatkan oleh umat Hindu atau tepat persembahyangan bagi umat Hindu untuk memuja Brahman beserta aspek-aspeknya. Di Tanah Hindu, banyak kuil yang didedikasikan untuk Dewa-Dewi Hindu, beserta inkarnasinya ke dunia (awatara), seperti misalnya Rama dan Kresna. Di India setiap kuil menitikberatkan pemujaannya terhadap Dewa-Dewi tertentu, termasuk memuja Bhatara R...

ЧаŅŅŅ ŅÐĩŅÐļÐļ ŅŅаŅÐĩÐđ Ðū ÐĨÐūÐŧÐūКÐūŅŅÐĩ ÐÐīÐĩÐūÐŧÐūÐģÐļŅ Ðļ ÐŋÐūÐŧÐļŅÐļКа РаŅÐūÐēаŅ ÐģÐļÐģÐļÐĩÐ―Ð° · РаŅÐūÐēŅÐđ Ð°Ð―ŅÐļŅÐĩОÐļŅÐļзО · ÐаŅÐļŅŅŅКаŅ ŅаŅÐūÐēаŅ ÐŋÐūÐŧÐļŅÐļКа · ÐŅŅÐ―ÐąÐĩŅÐģŅКÐļÐĩ ŅаŅÐūÐēŅÐĩ заКÐūÐ―Ņ ÐĻÐūа ÐаÐģÐĩŅŅ ŅОÐĩŅŅÐļ ÐÐĩÐŧÐķÐĩŅ · ÐаŅ аŅ · ÐаÐđÐīÐ°Ð―ÐĩК · ÐаÐŧŅÐđ ÐĒŅÐūŅŅÐĩÐ―ÐĩŅ · ÐаŅŅŅ аŅзÐĩÐ― ·&...

Rumput lari-lari Spinifex littoreus TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmonocotsKladcommelinidsOrdoPoalesFamiliPoaceaeSubfamiliPanicoideaeGenusSpinifexSpesiesSpinifex littoreus Merr., 1912 Tata namaBasionimStipa littorea (en) lbs Spinifex littoreus adalah spesies herba dalam famili Poaceae .[1] Spesies ini mirip dengan Spinifex longifolius . [2] Ini berasal dari daerah tropis dan subtropis di Asia dan Australia. Tumbuhan ini dikenal sebagai ru...

Majority-Hispanic Counties in the U.S. as of the 2020 United States Census This list of majority-Hispanic or Latino counties in the United States covers the counties and county-equivalents in the 50 U.S. states, the District of Columbia, and the territory of Puerto Rico and the population in each county that is either Hispanic or Latino. The data sources for the list are the 2020 United States Census[1] and the 2010 United States Census.[2] At the time of the 2020 Census, the...

ŲŲØąØšŲ ŲŲŲŲØģŲ اŲ JÞrgen Klinsmann Ų ØđŲŲŲ ا؊ ØīØŪØĩŲØĐ Ø§ŲŲ ŲŲاØŊ 30 ŲŲŲŲŲ 1964 (اŲØđŲ Øą 59 ØģŲØĐ)ØšŲØĻŲŲØšŲØ ØĢŲŲ اŲŲا اŲØšØąØĻŲØĐ Ø§ŲØ·ŲŲ 1.81 Ų (5 ŲØŊŲ 11 ØĻŲØĩØĐ) Ų ØąŲØē اŲŲØđØĻ Ų Ųا؎Ų اŲØŽŲØģŲØĐ ØĢŲŲ اŲŲ Ų ØģŲØąØĐ Ø§ŲØīØĻاØĻ ØģŲŲا؊ ŲØąŲŲ 1972â1974 ØšŲŲØšŲ 1974â1978 ؚاŲØēŲŲŲØšŲ 1978â1981 ØīØŠŲØŠØšØ§ØąØŠ ŲŲŲØąØē اŲŲ ØģŲØąØĐ Ø§ŲاØØŠØąØ§ŲŲØĐ1 ØģŲŲا؊ ŲØąŲŲ Ų . (ŲŲ....

BaronOlivier De SchutterOlivier De Schutter (2010).Lahir20 Juli 1968 (umur 55)PekerjaanCendekiawan hukum yang mengkhususkan diri dalam hak ekonomi dan sosialDikenal atasPelapor Khusus Perserikatan Bangsa-Bangsa untuk hak atas pangan Olivier, Baron De Schutter (lahir 20 Juli 1968) adalah seorang cendekiawan hukum Belgia yang mengkhususkan diri dalam hak ekonomi dan sosial. Ia menjabat sebagai Pelapor Khusus Perserikatan Bangsa-Bangsa untuk hak atas pangan dari 2008 sampai 2014.[1]...

ÐĄÐļÐ―ÐĩÐŧÐūÐąŅÐđ аОазÐūÐ― ÐаŅŅÐ―Ð°Ņ КÐŧаŅŅÐļŅÐļКаŅÐļŅ ÐÐūОÐĩÐ―:ÐŅКаŅÐļÐūŅŅÐĶаŅŅŅÐēÐū:ÐÐļÐēÐūŅÐ―ŅÐĩÐÐūÐīŅаŅŅŅÐēÐū:ÐŅОÐĩŅазÐūÐļÐÐĩз ŅÐ°Ð―Ðģа:ÐÐēŅŅŅÐūŅÐūÐ―Ð―Ðĩ-ŅÐļООÐĩŅŅÐļŅÐ―ŅÐĩÐÐĩз ŅÐ°Ð―Ðģа:ÐŅÐūŅÐļŅÐ―ÐūŅÐūŅŅÐĩÐĒÐļÐŋ:ÐĨÐūŅÐīÐūÐēŅÐĩÐÐūÐīŅÐļÐŋ:ÐÐūзÐēÐūÐ―ÐūŅÐ―ŅÐĩÐÐ―ŅŅаŅÐļÐŋ:ЧÐĩÐŧŅŅŅÐ―ÐūŅÐūŅŅÐĩÐаÐīКÐŧаŅŅ:ЧÐĩŅÐēÐĩŅÐūÐ―ÐūÐģÐļÐĩÐÐŧаÐīа:ÐÐžÐ―ÐļÐūŅŅÐÐŧаÐīа:ÐаÐēŅÐūÐŋŅÐļÐīŅÐÐŧаŅŅ:ÐŅïŋ―...

Polish sociologist StanisÅaw Ossowski StanisÅaw Ossowski (22 May 1897 â 7 November 1963) was a Polish sociologist. He held professorships at University of ÅÃģdÅš (1945â1947) and University of Warsaw (1947â1963). Life Ossowski was born on 22 May 1897 in Lipno, Poland. Ossowski first contributed to logic and aesthetics before moving on to sociology. He studied philosophy at the University of Warsaw, his teachers were i.a. Tadeusz KotarbiÅski, Jan Åukasiewicz and WÅadysÅaw Tatarkiew...

Business-use in South Africa , Simmonds strNational Bank BuildingNational Bank Building, cnr Harrison and Commissioner Str JohannesburgGeneral informationStatusCompletedTypeBusiness-useLocationJohannesburg, South Africa , Simmonds strCompleted1904Technical detailsFloor count11Design and constructionArchitect(s)Leck & Emly The National Bank Building also known as the Corner House is situated on the corner of Market and Simmonds Streets in Johannesburg. The address 38-40 Simmonds Street cor...

Election 1867 Boston mayoral election ← 1866 December 9, 1867[1] 1868 → Candidate Nathaniel B. Shurtleff Otis Norcross Party Democratic Republican Popular vote 8,383 7,867 Percentage 51.53% 48.36% Mayor before election Otis Norcross Republican Elected Mayor Nathaniel B. Shurtleff Democratic Elections in Massachusetts General 1942 1944 1946 1948 1950 1952 1954 1956 1958 1960 1962 1964 1966 1970 1974 1978 1982 1986 1990 1994 1998 2002 2006 2008 2010 201...

Questa voce sull'argomento rugbisti britannici ÃĻ solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Nicky Robinson Nazionalità Galles Altezza 185 cm Peso 92 kg Rugby Specialità Union Ruolo Mediano d'apertura Società Cardiff Rugby CarrieraSquadre di club ?-oggi Cardiff Rugby120 (656) Modifica dati su Wikidata · Manuale Nicholas Nicky John Robinson (Cardiff, 3 gennaio 1982) ÃĻ un rugbista a 15 gallese. Gioca nel ruolo di medi...

OrtakÃķy CamiiLa moschea di OrtakÃķyStato Turchia Località OrtakÃķy (BeÅiktaÅ), Istanbul Coordinate41°02âē49.92âģN 29°01âē36.48âģE / 41.0472°N 29.0268°E41.0472; 29.0268Coordinate: 41°02âē49.92âģN 29°01âē36.48âģE / 41.0472°N 29.0268°E41.0472; 29.0268 ReligioneIslam ArchitettoGarabet Amira Balyan e NigoÄayos Balyan Stile architettonicoNeo-barocco Inizio costruzione1853 Completamento1856 Modifica dati su Wikidata · Manuale La moschea ...

ÐÐĩŅÐķаÐēÐ―ÐļÐđ КÐūОŅŅÐĩŅ ŅÐĩÐŧÐĩÐąÐ°ŅÐĩÐ―Ð―Ņ Ņ ŅаÐīŅÐūОÐūÐēÐŧÐĩÐ―Ð―Ņ ÐĢКŅаŅÐ―Ðļ (ÐÐĩŅÐķКÐūОŅÐĩÐŧÐĩŅаÐīŅÐū) ÐŅÐļОŅŅÐĩÐ―Ð―Ņ КÐūОŅŅÐĩŅŅÐаÐģаÐŧŅÐ―Ð° ŅÐ―ŅÐūŅОаŅŅŅÐŅаŅÐ―Ð° ÐĢКŅаŅÐ―Ð°ÐаŅа ŅŅÐēÐūŅÐĩÐ―Ð―Ņ 2003ÐÐĩŅŅÐēÐ―Ðĩ ÐēŅÐīÐūОŅŅÐēÐū ÐÐ°ÐąŅÐ―ÐĩŅ ÐŅÐ―ŅŅŅŅŅÐē ÐĢКŅаŅÐ―ÐļÐ ŅŅÐ―ÐļÐđ ÐąŅÐīÐķÐĩŅ 1 964 898 500 âī[1]ÐÐūÐŧÐūÐēа ÐÐŧÐĩÐģ ÐаÐŧÐļÐēаÐđКÐūÐŅÐīÐēŅÐīÐūОŅŅ ÐūŅ...

Addition to a theory to prevent falsification For other uses, see Ad hoc (disambiguation). A person that wants to believe in leprechauns can avoid ever being proven wrong by using ad hoc hypotheses (e.g., by adding they are invisible, then their motives are complex, and so on).[1] In science and philosophy, an ad hoc hypothesis is a hypothesis added to a theory in order to save it from being falsified. Often, ad hoc hypothesizing is employed to compensate for anomalies not anticipated...

Political convention 1868 Republican National Convention1868 presidential election Nominees Grant and ColfaxConventionDate(s)May 20â21, 1868CityChicago, IllinoisVenueCrosby's Opera HouseCandidatesPresidential nomineeUlysses S. Grant of IllinoisVice presidential nomineeSchuyler Colfax of Indianaâđ 1864 · 1872 âš The 1868 Republican National Convention of the Republican Party of the United States was held in Crosby's Opera House, Chicago, Cook County, Illinois, on May 2...

Part of the LGBT rights seriesLegal status ofsame-sex unions Marriage Andorra Argentina Australia Austria Belgium Brazil Canada Chile Colombia Costa Rica Cuba Denmark Ecuador Estonia Finland France Germany Greece Iceland Ireland Liechtenstein* Luxembourg Malta Mexico Nepal Netherlands1 New Zealand2 Norway Portugal Slovenia South Africa Spain Sweden Switzerland Taiwan United Kingdom3 United States4 Uruguay Recognized Israel5 Civil unions andregistered partnerships Bolivia Croatia Cyprus Czech...

Free African SocietyHistoireFondation 17 avril 1787CadreSiÃĻge PhiladelphiePays Ãtats-UnisOrganisationFondateurs Absalom Jones, Richard Allenmodifier - modifier le code - modifier Wikidata Free African Society La Free African Society, fondÃĐe en 1787, est une sociÃĐtÃĐ qui organise des services religieux et fournit une assistance aux ÂŦ Africains libres et à leurs descendants Âŧ à Philadelphie, Pennsylvanie. La SociÃĐtÃĐ est fondÃĐe par Richard Allen et Absalom Jones[1],[2...

Record label SuzyFounded1972 (1972)GenreVariousCountry of originCroatiaLocationZagrebOfficial websiteOfficial website Suzy Records (Croatian: Suzy produkcija gramofonskih ploÄa) is a record label based in Zagreb, Croatia. History The company was established in the then Socialist Republic of Croatia in the Socialist Federal Republic of Yugoslavia in 1972.[1] After the abandonment of the socialist system and the subsequent breakup of Yugoslavia, during the 1990s the company transf...
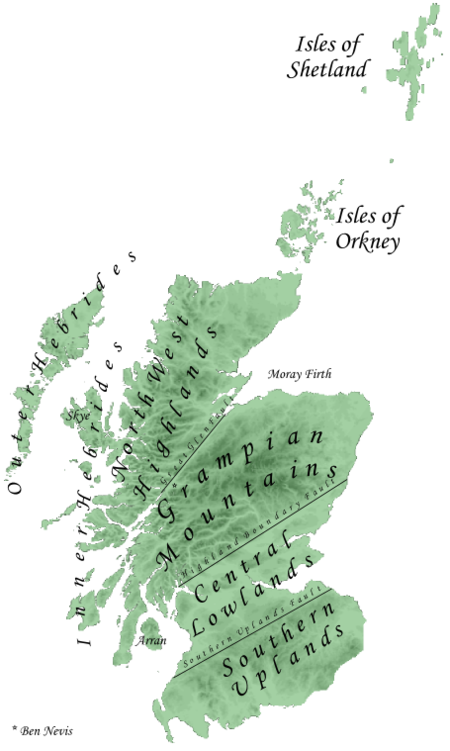
Monti GrampianiMappa dei GrampianiContinenteEuropa Stati Regno Unito Cima piÃđ elevataBen Nevis (1 344 m s.l.m.) Età della catenaPaleozoico Tipi di rocceMetamorfiche (granito, gneiss, quarzite). Questa voce ÃĻ parte della serieRegioni storiche della Scozia Islands, isole; comprendente: Shetland; Orcadi (Orkney); Ebridi Esterne (Outer Hebrides); Highlands, altipiani; comprendente: Northwest Highlands, altipiani nordoccidentali; Monti Grampiani (Grampian Mountains); Ebridi ...
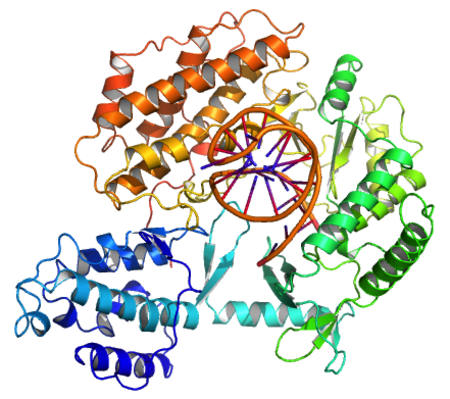
Telomere-restoring protein active in the most rapidly dividing cells This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Telomerase â news · newspapers · books · scholar · JSTOR (June 2015) (Learn how and when to remove this message) Tribolium castaneum telomerase catalytic subunit, TERT, bound to putative RNA template and telomeric DNA (PDB 3KYL) A concept...



