Átmeneti állapot
|
Read other articles:

Dany Nounkeu Dany membela Galatasaray pada tahun 2012.Informasi pribadiNama lengkap Dany Achille Nounkeu TchounkeuTanggal lahir 11 April 1986 (umur 37)Tempat lahir Yaoundé, KamerunTinggi 1,84 m (6 ft 1⁄2 in)Posisi bermain BekInformasi klubKlub saat ini GalatasarayNomor 24Karier junior Collège Vogt AtleticKarier senior*Tahun Tim Tampil (Gol)2005–2006 FC Metz B 13 (0)2006–2008 CSO Amnéville 16 (3)2008–2009 Pau FC 24 (0)2009–2010 Toulouse 18 (0)2010–2012 G...

Danau TekapoDanau TekapoLetakDistrik Mackenzie, region Canterbury, Pulau SelatanKoordinat43°53′S 170°31′E / 43.883°S 170.517°E / -43.883; 170.517Koordinat: 43°53′S 170°31′E / 43.883°S 170.517°E / -43.883; 170.517Aliran masuk utamaSungai Godley (utara), Sungai Macauley (utara), Sungai Mistake (barat), Sungai Cass (barat)[1]Aliran keluar utamaSungai TekapoWilayah tangkapan air1.463 km2 (565 sq mi)[1]T...

Tengku Hassanal Ibrahim Alam Shahتڠکو حسن الإبراهيم عالم شاهTengku Mahkota PahangTengku Mahkota PahangBerkuasa22 Januari 2019 – sekarangProklamasi29 Januari 2019PendahuluTengku AbdullahPemangku Raja PahangBerkuasa31 Januari 2019 – 31 Januari 2024Proklamasi29 Januari 2019PendahuluTengku AbdullahMenteri BesarWan Rosdy Wan IsmailTengku Panglima Besar PahangBerkuasa18 Juni 2018 – 22 Januari 2019PendahuluTengku Ibrahim bin Tengku SulaimanPenerusTengku AzlanInformasi pr...

Resolusi 504Dewan Keamanan PBBChadTanggal30 April 1982Sidang no.2.358KodeS/RES/504 (Dokumen)TopikChadHasilDiadopsiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Britania Raya Amerika Serikat Uni SovietAnggota tidak tetap Spanyol Guyana Irlandia Yordania Jepang Panama Polandia Togo Uganda Zaire Resolusi 504 Dewan Keamanan Perserikatan Bangsa-Bangsa, diadopsi pada 30 April 1982. Usai menerima perwakilan...

Kostas Stafylidis Informasi pribadiNama lengkap Konstantinos StafylidisTanggal lahir 2 Desember 1993 (umur 30)Tempat lahir Thessaloniki, YunaniTinggi 1,78 m (5 ft 10 in)Posisi bermain Bek kiri / Sayap kiriInformasi klubKlub saat ini AugsburgNomor 3Karier junior2006–2011 PAOKKarier senior*Tahun Tim Tampil (Gol)2011–2012 PAOK 16 (0)2012–2015 Bayer Leverkusen 1 (0)2012–2013 → PAOK (pinjaman) 21 (1)2014–2015 → Fulham (pinjaman) 38 (0)2015– Augsburg 9 (1)Tim na...

Genesi GroupCompany typePrivateIndustryComputer hardware, Software, IT services, IT consultingFounded3 January 2003 FounderWilliam H. BuckRaquel VelascoHeadquartersSan Antonio, TexasMexico City, MexicoFrankfurt, GermanyArea servedWorldwideWebsitegenesi-tech.com Genesi is an international group of technology and consulting companies in the United States, Mexico and Germany. It is most widely known for designing and manufacturing ARM architecture and Power ISA-based computing devices. The ...

Australian television news show This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Studio 10 – news · newspapers · books · scholar · JSTOR (March 2020) (Learn how and when to remove this template message) Studio 10GenreMorning show, news, current affairsCreated byAdam BolandPresented by Sarah Harris Joe Hildebr...

Small nucleolar RNA SNORD63Predicted secondary structure and sequence conservation of SNORD63IdentifiersSymbolSNORD63Alt. SymbolsU63RfamRF00154Other dataRNA typeGene; snRNA; snoRNA; CD-boxDomain(s)EukaryotaGOGO:0006396 GO:0005730SOSO:0000593PDB structuresPDBe In molecular biology, snoRNA U63 (also known as SNORD63) is a non-coding RNA (ncRNA) molecule which functions in the modification of other small nuclear RNAs (snRNAs). This type of modifying RNA is usually located in the nucleolus of the...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапси...

1988 single by Morrissey This article is about the song. For the subculture, see Suedehead (subculture). For the album, see Suedehead: The Best of Morrissey. SuedeheadSingle by Morrisseyfrom the album Viva Hate B-side I Know Very Well How I Got My Name Hairdresser on Fire Oh Well, I'll Never Learn Released15 February 1988 (1988-02-15)[1]GenreJangle pop[2]Length3:54LabelHMVSongwriter(s) Morrissey Stephen Street Producer(s)Stephen StreetMorrissey singles chronolog...
Yahudi Aljazairيهود الجزائر Juifs d’AlgérieLokasi Aljazair di AfrikaJumlah populasi<200[1](2020)Daerah dengan populasi signifikanAljirBahasaArab, Prancis, BerberAgamaAgama YahudiKelompok etnik terkaitYahudi (YahudiMaghrebi) Yahudi-Aljazair merujuk kepada komunitas Yahudi di Aljazair, yang bermula sejak abad ke-1 Masehi. Pada abad ke-15, sebagian besar Yahudi Spanyol kabur ke Maghreb, yang meliputi Aljazair pada saat ini, usai pengusiran dari Spanyol dan Portugal; bebe...

Aquaman 2 beralih ke halaman ini. Untuk Iterasi komik Aquaman II, lihat Aquaman § Biografi_karakter_fiksi. Aquaman and the Lost KingdomPoster rilis teaterSutradaraJames WanProduser Peter Safran James Wan Rob Cowan SkenarioDavid Leslie Johnson-McGoldrickCerita James Wan David Leslie Johnson-McGoldrick Jason Momoa Thomas Pa'a Sibbett BerdasarkanKarakterdari DCPemeran Jason Momoa Patrick Wilson Amber Heard Yahya Abdul-Mateen II Randall Park Dolph Lundgren Temuera Morrison Martin Short Nico...

2012 science-fantasy webcomic Ava's DemonLogo used for the Kickstarter campaignAuthor(s)Michelle Czajkowski FusWebsitewww.avasdemon.comCurrent status/scheduleSporadic[1]Launch date2012Genre(s)Sci-fi, Fantasy Ava's Demon is a science fantasy webcomic written and drawn by Michelle Czajkowski Fus and colored by a number of colorists. The comic, which has been ongoing since 2012, is known for its painted art style and animations. The first physical publication of Ava's Demon was released ...

نيا ميخانيونا تقسيم إداري البلد اليونان [1] خصائص جغرافية إحداثيات 40°27′52″N 22°51′38″E / 40.46444444°N 22.86055556°E / 40.46444444; 22.86055556 الارتفاع 21 متر السكان التعداد السكاني 7846 (resident population of Greece) (2021)7155 (resident population of Greece) (2001)5678 (resident population of Greece) (1991)8775 (resident population o...

American comedy television series (2019–2022) DollfaceGenreComedyCreated byJordan WeissStarring Kat Dennings Brenda Song Shay Mitchell Esther Povitsky Music byJonathan SadoffCountry of originUnited StatesOriginal languageEnglishNo. of seasons2No. of episodes20ProductionExecutive producers Ira Ungerleider Jordan Weiss Kat Dennings Margot Robbie Tom Ackerley Brett Hedblom Bryan Unkeless Scott Morgan Nicole King Stephanie Laing Matt Spicer Josey McNamara Michelle Nader Producers Melanie J. Eli...

Pharmaceutical drug Not to be confused with Conjugated estrogens or Estrogen conjugate. Conjugated estriolEstriol 16α-glucuronide, the primary active component in conjugated estriol (estriol glucuronides constitute about 35 to 46% of total content).Estriol 3-sulfate, the second major active component in conjugated estriol (constitutes about 15 to 22% of total content).Combination ofEstriol glucuronideEstrogenEstriol sulfateEstrogenEstriol sulfate glucuronideEstrogenClinical dataTrade namesPr...

Pandémie de Covid-19 en AndorreMaladie Maladie à coronavirus 2019(Covid-19)Agent infectieux SARS-CoV-2Origine Wuhan (Hubei, Chine)Localisation AndorreDate d'arrivée Depuis le 2 mars 2020(4 ans, 5 mois et 2 jours)BilanCas confirmés 46 588 (au 5 novembre 2022)[1],[2]Cas soignés 46 319 (au 5 novembre 2022)[1],[2]Morts 155 (au 5 novembre 2022)[1],[2]modifier - modifier le code - modifier Wikidata La pandémie de Covid-19 est une crise sanitaire majeure provoquée par...
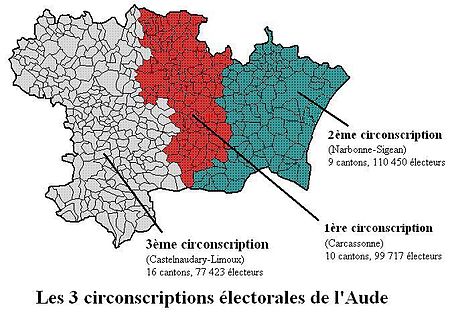
Les députés actuels actuels de l'Aude sont 3 membres du Rassemblement national : Christophe Barthès, Frédéric Falcon et Julien Rancoule. Les 3 circonscriptions de l'Aude Article connexe : Liste des circonscriptions législatives de l'Aude. L'Aude compte 3 circonscriptions : Cinquième République Dix-septième Législature (2024- ) Les députés élus le 7 juillet 2024 sont : Circonscription Député Parti Suppléant Autre mandat Première circonscription Christophe B...

This article is part of a series on theCinema ofAustralia List of Australian films Early years and the Silent film era pre 1910 1910s 1920s The war years and post-World War II 1930s 1940s 1950s 1960s 1970s 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 1980s 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990s 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000s 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010s 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020s 2020 2021 ...

