Általánosított Riemann-hipotézis
|
Read other articles:

Dino TimeTheatrical release posterSutradaraYoon-suk ChoiJohn KafkaProduserRobert AbramoffJoonbum HeoDavid LovegrenJae Y. MohJae Woo ParkSharath SurySkenarioJames GrecoZachary RosenblattAdam BeechenJae Woo ParkCeritaYoon-suk ChoiJohn KafkaPemeranPamela AdlonTara StrongJane LynchYuri LowenthalFred TatascioreMelanie GriffithRob SchneiderPenata musikStephen BartonLoren GoldSinematograferYoon-suk ChoiJohn KafkaPenyuntingDavid B. BaronBilly JonesPerusahaanproduksiCJ EntertainmentMyriad Pictur...
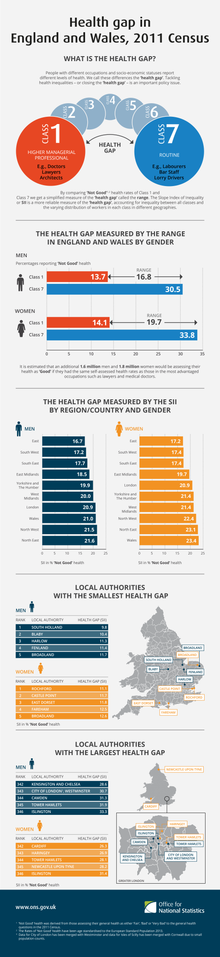
Kesenjangan kesehatan di Inggris dan Wales menurut sensus 2011 Kesetaraan kesehatan atau keadilan kesehatan (bahasa Inggris: health equity) adalah tidak adanya disparitas atau kesenjangan yang sistematis dalam kesehatan di antara kelompok-kelompok yang memiliki perbedaan keuntungan atau ketidakberuntungan sosial, seperti kekayaan, kekuasaan, atau prestise.[1] Orang-orang yang secara konsisten tidak memiliki ketiga faktor-faktor penentu tersebut mengalami kerugian kesehatan secara sign...

Johann Adam IPangeran LiechtensteinBerkuasa5 April 1684 – 16 Juni 1712PendahuluKarl EusebiusPenerusJosef WenzelInformasi pribadiKelahiran(1662-08-16)16 Agustus 1662BrnoKematian16 Juni 1712(1712-06-16) (umur 49)WinaPemakamanGereja Kelahiran Perawan Maria, BrnoWangsaLiechtensteinNama lengkapJohann Adam AndreasAyahKarl EusebiusIbuJohanna Beatrix von Dietrichstein-NikolsburgPasanganPutri Edmunda Maria dari Dietrichstein-Nikolsburg Hans-Adam I (Johann Adam Andreas; 16 Agustus 1662, di Brno&...

Liu Zhixun (Hanzi: 柳直荀; November 1898 – 14 September 1932), juga dikenal sebagai Liu Keming (Hanzi: 刘克明), adalah seorang anggota Tentara Merah Buruh dan Petani Tiongkok. Iaa disingkirkan oleh pemimpin Komunis Xia Xi dan dieksekusi.[1][2] Referensi ^ 李淑一50年苦寻柳直荀死因 ^ 柳直荀烈士死亡真相 Pengawasan otoritas Umum ISNI 1 VIAF 1 WorldCat Perpustakaan nasional Amerika Serikat Belanda Lain-lain Faceted Application of Subject Termino...

Artikel ini bukan mengenai Paym. PaytmMarkas besar Paytm di Noida.JenisPublikKode emitenNSE: PAYTMBSE: 543396ISININE982J01020Industri Teknologi keuangan Perdagangan elektronik DidirikanAgustus 2010; 13 tahun lalu (2010-08) di Noida, Uttar Pradesh, IndiaPendiriVijay Shekhar SharmaKantorpusatB-121, Sektor 5, Noida, Uttar Pradesh, IndiaWilayah operasiIndiaKanadaJepangTokohkunciVijay Shekhar Sharma (CEO)Amit Nayyar (Presiden)ProdukPaytm MallPaytm Payments BankPaytm MoneyPayPayGamepindPa...

Geoffroi I dari RennesKelahiranskt. 980Rennes, County Rennes, Kadipaten BretagneKematian20 November 1008Nantes, Loire-Atlantique, Pays de la Loire, PrancisPemakamanBretagneWangsaWangsa RennesAyahConan IIbuErmengarde dari AnjouPasanganHavoiseAnakAlain III dari BretagneEmme de Bretagne Eudes dari RennesAdela, Abdis St. GeorgesAgamaKatolik Roma Geoffroi I dari Rennes (skt. 980 – 20 November 1008), juga dikenal sebagai Geoffroi dari Bretagne dan Geoffroi Berengar, adalah putra tertua Adipati Co...

Disambiguazione – Se stai cercando l'omonimo architetto, vedi Tullio Rossi (architetto). Questa voce sull'argomento ciclisti italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Tullio Rossi Tullio Rossi con la Notari Presutti Splendor nel 1975 Nazionalità Italia Ciclismo Specialità Strada Termine carriera 1978 Carriera Squadre di club 1973-1974 Dreherforte1975Splendor1976 Furzi...

American college football season This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 2015 South Florida Bulls football team – news · newspapers · books · scholar · JSTOR (April 2015) 2015 South Florida Bulls footballMiami Beach Bowl, L 35–45 vs. Western KentuckyConferenceAmerican Athletic ConferenceD...

K. R. T. Wasitodiningrat K. R. T. Wasitodiningrat (Pak Cocro, * 17. März 1909 in Gunung Ketur, Yogyakarta; † 30. August 2007 in Yogyakarta) war ein indonesischer Rebab-Spieler im höfischen Orchester (Gamelan). Leben und Wirken Wasitodiningrat wurde als Cokrowasito (Tjokrowasito) geboren, wovon der Name Pak Cokro abgeleitet ist, unter dem er in den USA bekannt wurde. Seit den 1960er-Jahren hieß er K. R. T. Wasitodipuro (Kanjeng Raden Tumenggung Wasitodipuro), später erhielt er den Ehrenn...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

American blues singer-songwriter (1935–2017) For other people named James Cotton, see James Cotton (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: James Cotton – news · newspapers · books · scholar · JSTOR (March 2017) (Learn how and when to remove this message) James CottonCotton in 1981...

Pour l’article homonyme, voir Planète Océan (film). Vue d'artiste d'une planète-océan. Une planète-océan est un type hypothétique de planète qui serait intégralement recouverte d'un océan, d'eau ou éventuellement d'autres composés volatils, d'une profondeur variable mais pouvant être de plusieurs dizaines de kilomètres. Définition Initialement proposé par David J. Stevenson de l'Institut californien de technologie, ce modèle a été approfondi par l'équipe de Christophe S...

جماعة الدعوة والإصلاح في إيرانالشعارالتأسيسالنوع حزب سياسي البلد إيران التأسيس 1980 الشخصياتالقادة عبد الرحمن بيرانيالأفكارالأيديولوجيا سني إسلام، إخوان مسلمونمعلومات أخرىموقع الويب islahweb.org تعديل - تعديل مصدري - تعديل ويكي بيانات جماعة الدعوة والإصلاح في إيران والتي �...

مبنى يوروباEuropa buildingThe Europa building in Brussels, seen from across the Rue de la Loi/Wetstraat [لغات أخرى]التسميةأسماء سابقة Résidence Palace - Bloc Aمعلومات عامةنوع المبنى مبنى مقر عام المكان European Quarter (en) العنوان Rue de la Loi / Wetstraat [لغات أخرى] 155المنطقة الإدارية مدينة بروكسل البلد بلجيكا المدينة ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Sungai Majo Pusako, Kubu Babussalam, Rokan Hilir – berita · surat kabar · buku · cendekiawan · JSTOR Sungai Majo PusakoDesaNegara IndonesiaProvinsiRiauKabupatenRokan HilirKecamatanKubu BabussalamKod...

School district in McLean County, Illinois McLean County Unit District No. 5Address1809 West Hovey Avenue Normal, McLean County, Illinois, 61761United StatesCoordinates40°30′09″N 89°01′17″W / 40.502434°N 89.021343°W / 40.502434; -89.021343 (District office)District informationTypePublicMottoWorking together for quality public educationGradesK to 12EstablishedMay 8, 1948 (1948-May-08)SuperintendentMark DanielAsst. superintendent(s)Sand...

Shopping mall in Colorado, United StatesColorado MillsThe west entrance to the mallLocationLakewood, Colorado, United StatesCoordinates39°44′04″N 105°09′38″W / 39.734447°N 105.160430°W / 39.734447; -105.160430Address14500 W. Colfax AvenueOpening dateNovember 2002DeveloperMills CorporationManagementSimon Property GroupOwnerSimon Property Group (37.5%)No. of stores and servicesover 180No. of anchor tenants12Total retail floor area1,411,627 sq ft (13...

Colombian track cyclist Juliana GaviriaGaviria in 2020Personal informationFull nameJuliana Gaviria RendonBorn (1991-03-31) 31 March 1991 (age 33)La Ceja, Antioquia, ColombiaHeight1.65 m (5 ft 5 in)Weight58 kg (128 lb)Team informationCurrent team ColombiaDisciplineTrack cyclingRoleRiderRider typeSprinter Medal record Representing Colombia Women's track cycling Event 1st 2nd 3rd Nations Cup 1 0 0 Nations Cup stage 2 0 1 Pan American Games ...

Campionato europeo di roller derbySport roller derby TipoSquadre nazionali TitoloCampione d'Europa Aperturasettembre Chiusurasettembre Partecipanti8 (2014) FormulaEliminazione diretta Sito Internet[1] StoriaFondazione2014 Numero edizioni1 al 2014 Detentore Francia (1) Record vittorie Francia (1) Ultima edizioneTorneo europeo di roller derby 2014 Modifica dati su Wikidata · Manuale Il campionato europeo di roller derby è una competizione sportiva internazionale in cui si assegna il tito...

Street Fighter 6 Seni sampul yang menampilkan LukeDiterbitkan diPS4, PS5, Win, XSXSWW: 2 Juni 2023ArkadeJP: 2023GenrePertarunganLisensiLisensi proprietarium Model bisnisbuy-to-play (en) , season pass (en) dan battle pass (en) Bahasa Daftar bahasa Inggris dan bahasa Jepang 60 Karakteristik teknisPlatformWindows, PlayStation 4, PlayStation 5 dan Xbox Series X dan S MesinRE EngineModePermainan video pemain tunggal, permainan video multipemain, player versus player (en) dan multipemain berbagi la...







